树遍历
一棵 树 是图的一种特殊情况，因此上一章的 图遍历 算法也适用于树。图遍历可以从任何节点开始，但在树的情况下，遍历总是从根节点开始。二叉树可以以三种额外的遍历方式进行遍历。以下树将作为重复出现的示例。
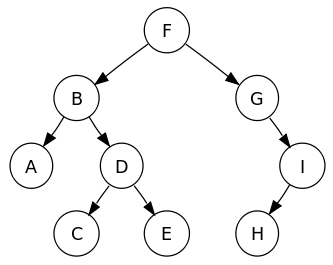
以广度优先顺序遍历树意味着，在访问节点 X 之后，将访问 X 的所有子节点，然后访问 X 的所有“孙子节点”（即子节点的子节点），然后访问 X 的所有“曾孙子节点”，等等。换句话说，树是通过扫描一层中的宽度来遍历的，然后再访问下一层，如动画所示
节点的子节点可以以任何顺序访问，但请记住算法使用队列，因此如果节点 X 在节点 Y 之前入队（在动画中为灰色），则 X 的子节点将在 Y 的子节点之前被访问（在动画中为黑色）。对于本章开头的示例树，两种可能的广度优先遍历是 F B G A D I C E H 和 F G B I D A H E C。在第二次遍历中，G 在 B 之前被访问，所以 I 在 A 和 D 之前被访问。
|
练习：广度优先遍历 列出相同树的另外两个可能的广度优先遍历。 答案 由于 F、B 和 D 每个都有两个子节点，因此总共有 2*2*2=8 种可能的广度优先遍历
第一个和最后一个遍历已经在上面给出，因此您可以列出任何其他两个。 |
顾名思义，深度优先遍历将尽可能地沿着树的一条分支向下遍历，即直到它在叶子上停止，然后再尝试其他分支。从同一个父节点开始的各种分支可以以任何顺序探索。对于示例树，两种可能的深度优先遍历是 F B A D C E G I H 和 F G I H B D E C A。
|
练习：广度优先遍历 列出相同树的另外两个可能的深度优先遍历。 答案 由于 F、B 和 D 每个都有两个子节点，因此总共有 2*2*2=8 种可能的深度优先遍历
第一个和最后一个遍历已经在上面给出，因此您可以列出任何其他两个。 |
|
练习：深度和广度优先遍历 列出此树的 一个 广度优先遍历和 一个 深度优先遍历： 答案 可能的深度优先遍历是
可能的广度优先遍历是
|
- 深度优先遍历通常使用堆栈
- 广度优先遍历通常使用队列
二叉树通常从左到右遍历，但从右到左的遍历也是可能的，并且可能会出现在考试问题中。因此，在本节的其余部分，我们将始终明确说明方向。
如果每个节点都在访问其两个子树 之前 被访问，则称为 先序 遍历。从左到右的先序遍历的算法是
- 访问根节点（通常输出它）
- 对左子树进行先序遍历
- 对右子树进行先序遍历
可以使用以下方法实现，使用前一个单元中定义的 树数据结构
sub PreOrder(TreeNode)
Output(TreeNode.value)
If LeftPointer(TreeNode) != NULL Then
PreOrder(TreeNode.LeftNode)
If RightPointer(TreeNode) != NULL Then
PreOrder(TreeNode.RightNode)
end sub
由于算法完全确定了访问节点的顺序，因此对于每个二叉树，只有一个可能的从左到右的先序遍历。对于我们的示例树，它是一个二叉树，它是 F B A D C E G I H。
由于先序遍历总是沿着一个分支（左或右）向下遍历，然后再移动到另一个分支，因此先序遍历始终是可能的深度优先遍历之一。
如果每个节点都在访问其子树 之后 被访问，则称为 后序 遍历。从左到右的后序遍历的算法是
- 对左子树进行后序遍历
- 对右子树进行后序遍历
- 访问根节点（通常输出它）
可以使用以下方法实现
sub PostOrder(TreeNode)
If LeftPointer(TreeNode) != NULL Then
PostOrder(TreeNode.LeftNode)
If RightPointer(TreeNode) != NULL Then
PostOrder(TreeNode.RightNode)
Output(TreeNode.value)
end sub
对于每个二叉树，只有一个从左到右的后序遍历。对于我们的示例树，它是 A C E D B H I G F。
如果每个节点都在访问其左子树和右子树 之间 被访问，则称为 中序 遍历。从左到右的中序遍历的算法是
- 对左子树进行中序遍历
- 访问根节点（通常输出它）
- 对右子树进行中序遍历
可以使用以下方法实现
sub InOrder(TreeNode)
If LeftPointer(TreeNode) != NULL Then
InOrder(TreeNode.LeftNode)
Output(TreeNode.value)
If RightPointer(TreeNode) != NULL Then
InOrder(TreeNode.RightNode)
end sub
对于每个二叉树，只有一个从左到右的中序遍历。对于我们的示例树，它是 A B C D E F G H I。请注意，节点是以升序访问的。这不是巧合。
在像我们的示例树这样的二叉搜索树中，左子树中的值小于根，右子树中的值大于根，因此从左到右的中序遍历将以升序访问节点。
|
练习：中序遍历 语句“中序遍历总是以升序访问节点”是真还是假？ 答案 它是错误的。中序遍历只有在它是从左到右的遍历 并且 树是二叉搜索树时，才会以升序访问节点。 如何更改上面的算法以按降序访问二叉搜索树的节点？ 答案 从右到左的中序遍历将产生所需的顺序
|
在考试中，你可能会被给出一些遍历伪代码和一棵二叉树，并被要求按照代码访问节点的顺序列出节点。
首先要仔细查看代码并检查
- 节点是在访问子树之前（先序）、之间（中序）还是之后（后序）访问的？
- 左子树是在右子树之前访问还是反过来？
例如，以下代码执行从左到右的遍历，注释显示了根节点的访问位置可能在哪里。
sub Traversal(TreeNode)
'Output(TreeNode.value) REM Pre-Order
If LeftPointer(TreeNode) != NULL Then
Traversal(TreeNode.LeftNode)
'Output(TreeNode.value) REM In-Order
If RightPointer(TreeNode) != NULL Then
Traversal(TreeNode.RightNode)
'Output(TreeNode.value) REM Post-Order
end sub
假设它是从左到右的遍历。一旦你知道从节点访问的位置，是先序、中序还是后序遍历，你就可以按照如下方式标注二叉树的每个节点：
| 遍历类型 | 输出代码位置 | 放置标记的位置 |
|---|---|---|
| 先序 | 顶部 | 左侧 |
| 中序 | 中间 | 底部 |
| 后序 | 底部 | 右侧 |
最后，围绕树逆时针画一条线，连接这些标记。沿着这条线，在遇到标记时写下每个节点：这将是代码访问节点的顺序。以下是三种可能的从左到右遍历。
- 三种不同类型的从左到右遍历
-
先序遍历
FBADCEGIH -
中序遍历
ABCDEFGHI -
后序遍历
ACEDBHIGF
如你所见，遵循这个技巧，你将得到与上面部分相同的答案。
如果遍历是从右到左，你必须画一条顺时针线，并交换先序或后序标记的位置。
| 遍历类型 | 输出代码位置 | 从左到右遍历的标记 | 从右到左遍历的标记 |
|---|---|---|---|
| 先序 | 顶部 | 左侧 | 右侧 |
| 中序 | 中间 | 底部 | 底部 |
| 后序 | 底部 | 右侧 | 左侧 |
如果树是二叉搜索树，并且要求你进行中序遍历，你应该按照升序（对于从左到右的遍历）或降序（对于从右到左的遍历）访问节点。如果它不是二叉搜索树，中序遍历不会按照升序或降序访问节点，但先序或后序遍历可能会，这将取决于节点在树中的位置。
虽然在本节中，为了清晰起见，我们始终明确地说明是左到右还是右到左遍历，但先序、中序和后序术语的典型用法隐含着左到右遍历，除非有相反的说明。
|
练习：二叉树遍历 对于以下二叉树，执行先序、中序和后序遍历。 答案 如果没有其他说明，则假定从左到右遍历。
以下代码描述了哪种遍历 sub Traverse(TreeNode)
If LeftPointer(TreeNode) != NULL Then
Traverse(TreeNode.LeftNode)
Output(TreeNode.value)
If RightPointer(TreeNode) != NULL Then
Traverse(TreeNode.RightNode)
end sub
答案 中序遍历，因为节点访问位于代码的中心，并且左子树在右子树之前遍历。 以下代码的作用是什么？ sub P(TreeNode)
If RightPointer(TreeNode) != NULL Then
P(TreeNode.RightNode)
If LeftPointer(TreeNode) != NULL Then
P(TreeNode.LeftNode)
Output(TreeNode.value)
end sub
答案 它执行从右到左的后序遍历，因为它首先访问右子树，然后访问左子树，最后访问节点。 使用以下二叉树
答案
|
.svg)