编程概念：图

图 - 用于模拟某个集合中对象之间关系的图表，由边（线）和顶点（点）组成

当两个顶点由一条边连接时，这两个顶点被称为邻居。顶点的度是指它连接到的其他顶点的数量（或它拥有的邻居数量）。图用于记录事物之间的关系。图的常见用途包括地图、社交网络、化学化合物和电路。我们将重点关注地图，其中图将用于模拟一些东英格兰城镇，并找到两个地点之间的最短距离，例如您手机上的方向查找GPS应用程序。下面是一个无向图（没有箭头），显示了东英格兰城镇的简化地图

东英格兰城镇之间的道路

在上图中，我们有 7 个顶点和 11 条边。Dunwich 与 Blaxhall 和 Harwich 相邻。Clacton 有 3 条边直接连接到 3 个其他顶点，因此它的度为 3。

练习：图 列出 Tiptree 的所有邻居 答案 Feering Maldon Clacton Harwich Tiptree 的度是多少 答案 4 Dunwich 的度是多少 答案 2 以下图有多少条边和顶点 答案 边 = 5 顶点 = 6

带标签或加权图

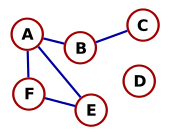
带标签的图与上图几乎相同，但边上附加了一些内容（通常是数值）。这在映射应用程序中很有用，当您想要找到顶点之间的最短距离或时间时。

东英格兰城镇之间的加权道路

练习：带标签或加权图 Harwich 和 Feering 之间的最短距离是多少？ 答案 Harwich 到 Tiptree = 31 Tiptree 到 Feering = 3 总计 = 34 Blaxhall 和 Clacton 之间的最短距离是多少？ 答案 Blaxhall 到 Harwich = 40 Harwich 到 Clacton = 17 总计 = 57 Maldon 和 Dunwich 之间的最短距离是多少？ 答案 Maldon 到 Feering = 11 Feering 到 Blaxhall = 46 Blaxhall 到 Dunwich = 15 总计 = 72 您可能还有 Maldon 到 Tiptree = 8 Tiptree 到 Feering = 3 Feering 到 Blaxhall = 46 Blaxhall 到 Dunwich = 15 总计 = 72 选择最佳路线是一项非常复杂的任务

有向图

一个有向图的例子

有向图与普通图非常相似，但不出所料，它们具有方向。您应该将它们视为城镇或城市中的道路系统。一些道路将是单行道，而其他道路则是双向的。这对我们的东英格兰交通系统有什么影响

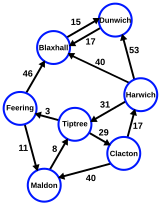东英格兰城镇之间的加权道路

练习：带标签或加权图 从 Maldon 到 Dunwich 的最短距离是多少？ 答案 Maldon 到 Tiptree = 8 Tiptree 到 Feering = 3 Feering 到 Blaxhall = 46 Blaxhall 到 Dunwich = 15 总计 = 72 现在此问题只有一个解决方案。 从 Harwich 到 Clacton 的最短距离是多少？ 答案 Harwich 到 Tiptree = 31 Tiptree 到 Clacton = 29 总计 = 60 从 Dunwich 到 Maldon 的最短距离是多少？ 答案 那个方向没有直达路线

无向图

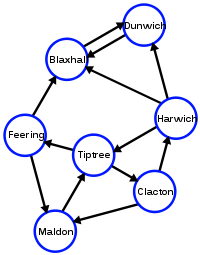
无向图不包含箭头，没有单行道。无向图可以是加权的或未加权的

无向且未加权	无向且加权	无向且未加权
		一个简单的图，包含三个 顶点和三条边。 每个顶点的度数为二， 因此这也是一个正则图。

无向图允许您沿每条边双向通行，它的工作方式与在每个顶点之间有两条边的有向图相同。请参见上文中的 Blaxhall 和 Dunwich。

简单图

在定义简单图之前，我们需要了解循环和多重边是什么

• 循环是指一个顶点与其自身连接的边
• 多重边是指两个顶点之间存在两个或多个连接

简单图	非简单图
这是一个简单图，因为它没有循环或多重边	这不是一个简单图 上述示例中的循环是指某人从 Dunwich 出发散步，最终回到 Dunwich 而没有访问任何其他顶点。 Harwich 和 Blaxhall 之间存在多重边，因为您可以乘渡轮或开车前往。

简单图 - 一个无向图，没有循环，并且任何两个不同顶点之间最多只有一条边

在一个具有 n 个顶点的简单图中，每个顶点的度数都小于 n。

简单图
无循环、无多重边、无方向

练习：简单图 给出简单图的定义 答案 它是一个无向图，没有循环，并且任何两个不同顶点之间最多只有一条边。 以下哪些图是简单图？ A B C D 答案 A B C D 否，因为它有一个循环（在 1 上） 是 否，因为它有一个多重边（FN）并且是有向的 否，它是方向的

如何在计算机上存储图

到目前为止，我们已经了解了如何使用边和顶点绘制图。如果要将它们存储为数字数据，则必须考虑一种对计算机友好的方式，因为计算机不擅长读取手绘图表。我们将研究两种方法：邻接矩阵和邻接表。

邻接矩阵

邻接矩阵记录每个顶点与所有其他顶点之间的关系。它同时记录两个顶点之间是否存在边以及不存在边的情况

无向-未加权	有向-未加权	无向-加权	有向-加权
B C D F H M T B 0 0 1 1 1 0 0 C 0 0 0 0 1 1 1 D 1 0 0 0 1 0 0 F 1 0 0 0 0 1 1 H 1 1 1 0 0 0 1 M 0 1 0 1 0 0 1 T 0 1 0 1 1 1 0	B C D F H M T B 0 0 1 0 0 0 0 C 0 0 0 0 1 1 0 D 1 0 0 0 0 0 0 F 1 0 0 0 0 1 0 H 1 0 1 0 0 0 1 M 0 0 0 0 0 0 1 T 0 1 0 1 0 0 0	B C D F H M T B ∞ ∞ 15 46 40 ∞ ∞ C ∞ ∞ ∞ ∞ 17 40 29 D 15 ∞ ∞ ∞ 53 ∞ ∞ F 46 ∞ ∞ ∞ ∞ 11 3 H 40 17 53 ∞ ∞ ∞ 31 M ∞ 40 ∞ 11 ∞ ∞ ∞ T ∞ 29 ∞ 3 31 ∞ ∞	B C D F H M T B ∞ ∞ 15 ∞ ∞ ∞ ∞ C ∞ ∞ ∞ ∞ 17 40 ∞ D 17 ∞ ∞ ∞ ∞ ∞ ∞ F 46 ∞ ∞ ∞ ∞ 11 ∞ H 40 ∞ 53 ∞ ∞ ∞ 31 M ∞ ∞ ∞ ∞ ∞ ∞ ∞ T ∞ 29 ∞ 3 ∞ ∞ ∞
两个顶点之间存在边 = 1 顶点之间不存在边 = 0		两个顶点之间存在边 = 使用权重 顶点之间不存在边 = ∞（无穷大符号）

优点

适用于边多于节点的图

缺点

不适用于边少于节点的图，因为它效率低下，会占用大量内存

邻接表

邻接表记录每个顶点与所有相关顶点之间的关系。它仅记录两个顶点之间是否存在边。

无向-未加权	有向-未加权	无向-加权	有向-加权
连接到 Blaxhall D; H; F Clacton H; M; T Dunwich B; H Feering B; M; T Harwich B; C; D; T Maldon C; F; T Tiptree C; F; H; M	连接到 Blaxhall D Clacton H; M Dunwich B Feering B; M Harwich B; D; T Maldon T Tiptree C; F	连接到 Blaxhall D,15; H,40; F,46 Clacton H,17; M,40; T,29 Dunwich B,15; H,53 Feering B,46; M,11; T,3 Harwich B,40; C,17; D,53; T,31 Maldon C,40; F,11; T,8 Tiptree C,29; F,3; H,31; M,8	连接到 Blaxhall D,15 Clacton H,17; M,40 Dunwich B,17 Feering B,46; M,11 Harwich B,40; D,53; T,31 Maldon T,8 Tiptree C,29; F,3
列出每个连接		列出每个连接以及权重

优点

适用于边数少于节点数的图

缺点

不适用于边数多于节点数的图，因为它效率低下并占用大量内存

练习：邻接矩阵和邻接表 为以下图绘制邻接表和邻接矩阵 答案 A B C D E F A 0 1 0 0 1 1 B 1 0 1 0 0 0 C 0 1 0 0 0 0 D 0 0 0 0 0 0 E 1 0 0 0 0 1 F 1 0 0 0 1 0 连接到 A B; E; F; B A; C C B D E A; F F A; E 为以下图绘制邻接表和邻接矩阵 答案 1 2 3 4 5 6 1 1 1 0 0 1 0 2 1 0 1 0 1 0 3 0 1 0 1 0 0 4 0 0 1 0 1 1 5 1 1 0 1 0 0 6 0 0 0 1 0 0 连接到 1 1; 2; 5 2 1; 3; 5 3 2; 4 4 3; 5; 6 5 1; 2; 4 6 4 为以下图绘制邻接表和邻接矩阵 答案 1 2 3 4 1 0 1 0 1 2 0 0 0 1 3 1 1 0 0 4 0 0 1 0 连接到 1 2; 4 2 4 3 1; 2 4 3 为以下图绘制邻接表和邻接矩阵 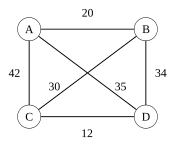答案 A B C D A ∞ 20 42 35 B 20 ∞ 30 34 C 42 30 ∞ 12 D 35 34 12 ∞ 连接到 A B,20; C,42; D,35 B A,20; C,30; D,34 C A,42; B,30; D,12 D A,35; B,34; C,12 为以下邻接表绘制图形 连接到 A B B A; C; D C B; D D B; C 答案 为以下邻接表绘制图形 连接到 A C,12; D,60 B A,10 C B,20; D,32 D B,22 E A,7 答案 为以下邻接矩阵绘制图形 A B D F N A 0 0 1 1 0 B 0 0 0 1 1 D 0 0 1 0 1 F 1 0 1 0 0 N 0 0 1 0 0 答案 为以下邻接矩阵绘制图形 A B D F N A ∞ 14 ∞ ∞ ∞ B ∞ ∞ 23 13 ∞ D 5 ∞ ∞ ∞ ∞ F 43 ∞ ∞ ∞ 33 N ∞ 22 ∞ 11 ∞ 答案 什么时候你会使用邻接表而不是邻接矩阵？ 答案 对于连接数较少的图，邻接表占用更少的空间。 什么时候你会使用邻接矩阵而不是邻接表？ 答案 当图有很多连接时，邻接矩阵更可取。