编程概念：递归技术

递归 - 用自身定义子例程。

递归是计算机科学中的一个关键领域，它依赖于您能够通过解决同一问题的越来越小的实例来解决问题。

一种称为Droste 效应 的递归的可视形式。此图像中的女士拿着一个物体，该物体包含她拿着相同物体的较小图像，该物体又包含她拿着相同物体的更小图像，以此类推。

名称中递归的一个例子是GNU 操作系统，您可能会问 GNU 代表什么

GNU = GNU 不是Unix

等一下，他们用重新说明名称来定义名称！

GNU

GNU 不是 Unix

GNU 不是 Unix 不是 Unix

GNU 不是 Unix 不是 Unix 不是 Unix

GNU 不是 Unix 不是 Unix 不是 Unix 不是 Unix

无限地

幸运的是，对于我们来说，使用计算机代码，我们的递归应该趋向于结束，因为我们正在解决同一问题的越来越小的实例，我们应该趋向于结束。在 GNU 示例中，名称始终保持相同的大小，但在以下示例中，有一个结束

示例：一个递归的故事 function revise(essay) { read(essay); get_feedback_on(essay); apply_changes_to(essay); revise(essay) unless essay.complete?; } 这是描述修改论文过程的伪代码，修改过程包括阅读论文、获取反馈、应用更改，然后修改略微更好的论文。你不断这样做，直到论文完成。

让我们看看一些计算机科学示例

阶乘示例

一个经典的计算机递归过程示例是用于计算阶乘 的函数自然数

$n!=n\times (n-1)\times (n-2)\times ...\times 1$

例如

$3!=3\times 2\times 1=6\$

$5!=5\times 4\times 3\times 2\times 1=120\$

$10!=10\times 9\times 8\times 7\times 6\times 5!=3628800\$

您注意到我在最终解决方案中做了什么吗？我没有写 5 * 4 * 3 * 2 * 1，而是使用了 5!，它产生 了相同的结果。回顾一下我们为什么使用递归的定义，我们似乎通过解决同一问题的较小实例来解决大问题，因此阶乘非常适合递归

10! = 10 * 9!
9! = 9 * 8!
8! = 8 * 7!
7! = 7 * 6!
6! = 6 * 5!
5! = 5 * 4!
4! = 4 * 3!
3! = 3 * 2!
2! = 2 * 1!
1! = 1

正如我们所看到的，每个 n! 都是 n * (n-1)! 的乘积。总之

$\operatorname {fact} (n)={\begin{cases}1&{\mbox{if }}n=1\\n\cdot \operatorname {fact} (n-1)&{\mbox{if }}n>1\\\end{cases}}$

伪代码 （递归）
function factorial is: input: integer n such that n >= 1 output: [n × (n-1) × (n-2) × … × 1] 1. if n is >= 1, return [ n × factorial(n-1) ] 2. otherwise, return 1 end factorial

现在让我们看看如何编写代码来解决这个问题

function factorial(ByVal n as integer)
  if n >= 1 then
    return n * factorial(n-1) 'recursive call
  else
    return 1
  end if
end function

sub main()
  console.writeline(factorial(10))
end sub

它看起来非常简单和优雅。但是它是如何工作的呢？

递归如何计算 factorial(4) 的图表

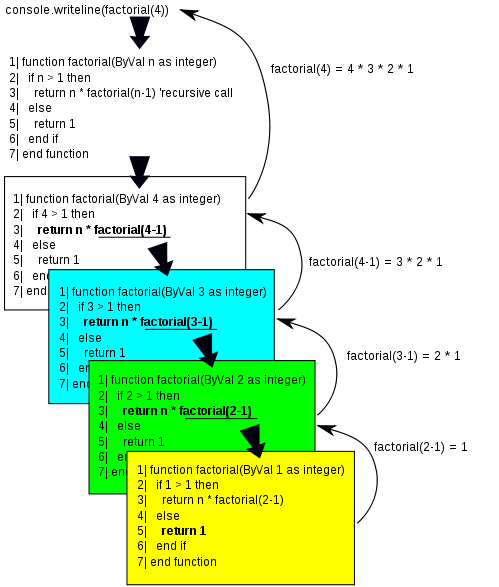
让我们建立一个跟踪表并看看发生了什么。这个跟踪表将不同于您以前建立的跟踪表，因为我们将不得不使用一个堆栈。如果您还没有阅读过关于堆栈 的内容，您必须在继续之前这样做

函数调用	n	返回行
1	4

到目前为止一切都很好，直到我们到达第 3 行。现在我们该怎么办？我们很快就会有两个 n 值，一个用于函数调用 1，另一个用于函数调用 2。使用跟踪表作为堆栈（堆栈底部在顶部，堆栈顶部在底部），我们将保存关于函数调用的所有数据，包括它的 n 值，并记下我们在完成 factorial(3) 后需要返回到的行。

函数调用	n	返回行
1	4	3
2	3

现在我们有了类似于以前的情况，让我们存储返回地址并转到 factorial(2)

函数调用	n	返回行
1	4	3
2	3	3
3	2

现在我们有了类似于以前的情况，让我们存储返回地址并转到 factorial(1)

函数调用	n	返回行	返回值
1	4	3
2	3	3
3	2	3
4	1		1

现在我们遇到了另一个问题，我们找到了 factorial(1) 的结束。我们接下来去哪一行？由于我们将跟踪表视为堆栈，我们将从顶部弹出上一个值，并查看我们存储的最后一个函数调用，即函数调用 3，factorial(2)，我们甚至知道要返回到的行，即第 3 行

return 2 * factorial(1)

我们知道从上一个返回值看 factorial(1) = 1。因此 factorial(2) 返回 2 * 1 = 2

函数调用	n	返回行	返回值
1	4	3
2	3	3
3	2	3	2
4	1		1

我们再次从堆栈中弹出最后一个函数调用，留下函数调用 2，factorial(3) 和第 3 行。

return 3 * factorial(2)

我们知道从上一个返回值看 factorial(2) = 2。因此 factorial(3) 返回 3 * 2 = 6

函数调用	n	返回行	返回值
1	4	3
2	3	3	6
3	2	3	2
4	1		1

我们再次从堆栈中弹出最后一个函数调用，留下函数调用 1，factorial(4) 和第 3 行。

return 4 * factorial(3)

我们知道从前面的返回值 factorial(3) = 6。因此 factorial(4) 返回 4 * 6 = 24。

函数调用	n	返回行	返回值
1	4	3	24
2	3	3	6
3	2	3	2
4	1		1

我们到达了函数调用 1 的末尾。但是我们现在要去哪里呢？堆栈上没有剩下任何东西，我们已经完成了代码。因此结果是 24。

斐波那契数列示例

斐波那契数列在自然界中被发现，几个世纪以来一直吸引着数学家。

另一个很好的例子是计算 斐波那契数列 的方法。根据定义，前两个斐波那契数列为 0 和 1，并且每个后续数字都是前两个数字的总和。

$0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\;\ldots \;$

例如，取第 6 个数字 5。这是第 5 个数字 3 和第 4 个数字 2 的总和。

在数学术语中，斐波那契数列 F_n 由递归语句定义

$F_{n}=F_{n-1}+F_{n-2},\!\,$

前两个值为

$F_{0}=0\quad {\text{and}}\quad F_{1}=1.$

让我们尝试创建一个代码版本

答案
function fib(n as integer) select case n case 0 return 0 case 1 return 1 case else return fib(n-1) + fib(n-2) end select end function

递归总结

但是，递归确实存在一些问题，请考虑我们仅仅为 4 个函数调用在堆栈上存储了多少数据。如果我们要执行 1000 次，使用的内存将非常大。

递归可以为问题产生更简单、更自然的解决方案

递归占用大量计算机资源来存储返回地址和状态

练习：递归 定义递归 答案 用自身来定义一个子例程 给出以下递归函数调用 recur(6) 的输出。 function recur(ByVal n as integer) console.writeline(n) if n > 0 then recur(n-1) else return 0 end if end function 答案 6 5 4 3 2 1 0 给出以下递归函数调用 recur(4) 的输出。 function recur(ByVal n as integer) if n > 0 then recur(n-1) else return 0 end if console.writeline(n) end function 答案 1 2 3 4 给出以下递归函数调用 recur(6) 的输出。 function recur(ByVal n as integer) if n <= 10 then recur(n+1) else return 0 end if console.writeline(n) end function 答案 10 9 8 7 6 为以下递归函数绘制一个跟踪表。 答案 说出递归解决方案的一个优点和一个缺点。 答案 递归可以为问题产生更简单、更自然的解决方案。 递归占用大量计算机资源来存储返回地址和状态。