计算理论：有限状态机

有限状态机

有限状态机是一种抽象形式（为什么/如何？）。它通过显示系统可以处于的每个状态以及每个状态之间的转换来模拟系统的行为。

考虑一台电梯 

系统的可能状态

'静止在 1 楼'，'向上移动'，'静止在 2 楼'，'向下移动'

[此处插入状态图片]

转换及其输入

• 从 '静止在 1 楼' 到 '向上移动' 由 '向上按钮' 触发
• 从 '向上移动' 到 '静止在 2 楼' 由 '到达 2' 触发
• 从静止在 2 楼到 '向下移动' 由 '向下按钮' 触发
• 从 '向下移动' 到 '静止在 1 楼' 由 '到达 1' 触发

从上面我们可以画出电梯的有限状态机。

[此处插入完成的有限状态机图片]

我们也可以制作一个状态转移表（定义这个语言框？）。

[此处插入状态转移图图片]

将系统表示为有限状态机非常强大，因为该模型允许我们非常清楚地展示行为。我们可以证明该系统是健壮的，并且不会以任何意外的方式运行。考虑电梯的示例：通过将系统建模为有限状态机，可以证明电梯无法在没有停止的情况下向上和向下移动。这是因为设计清楚地表明，从状态 '向上移动' 到状态 '向下移动' 的转换是不可能的。

有限状态机在许多科学领域都有应用。主要是工程学、生物学，最常见的是语言学，它们被用来描述语言。

接受二进制输入的有限状态自动机

从上面的图中我们可以看到它从状态 S1 开始，输入 1 将使其保持在状态 S1，输入 0 将使其移动到状态 S2。一旦进入 S2，输入 1 将使其保持在那里，输入 0 将使其切换回 S1。这意味着以下输入是有效的

110011001
001110011

它似乎可以接受任何二进制值，但事实并非如此。它唯一可以接受的状态是状态 S1。这给所有接受的输入施加了以下规则：“包含偶数个零的二进制数字组合”。这对于奇偶校验很有用。如果我尝试以下操作

110011011

我卡在状态 S2 并且 FSM 没有接受。你能创建一个 FSM 仅接受具有奇数个 1 的二进制数字吗？

练习：有限状态自动机 对于上面的 FSM，以下哪些输入是有效的 aaacdb ababacdaaac abcdb acda acdbdb 答案 aaacdb（正确） ababacdaaac（正确） abcdb（错误，没有输入可以接受 b 然后 c） acda（错误，S1 不是接受状态） acdbdb（正确） 对于上面的 FSM，以下哪些输入是有效的 987654321+994-0 5-5+2*4 9+8+7+6+5+4+3+2+1 0+1+2+1+ 99+88-77 答案 987654321+994-0（正确） 5-5+2*4（错误，没有输入 *） 9+8+7+6+5+4+3+2+1（正确） 0+1+2+1+（错误，S3 不是接受状态） 99+88-77（正确） 绘制一个有限状态自动机，它将接受单词 Banana 同时仅使用 3 个状态 答案 绘制一个单独的有限状态自动机，它将接受所有单词 Tim Grit Grrrrrim 答案

米利机

米利机 - 带有输出的 FSM

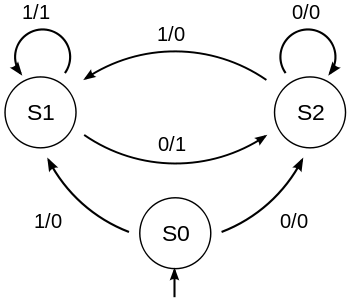
一些 FSM 会根据状态和输入值输出值

上面的米利机为每个输入输出一个值。你可以通过以下方式区分它们：输入 / 输出。因此对于以下输入

000101010

它输出

000010101

移位所有位到右边，并将二进制数字输入除以二。

练习：米利机 对于上面的米利机，以下输入会输出什么 50 20,10,20 10,10,10,20 这台机器做什么，输出告诉你什么？ 答案 0 30,20,0 40,30,20,0 这台机器可以用来跟踪进入自动售货机的钱，让你知道在购买 50 便士的巧克力棒时你还有多少钱要付 米利机和有限状态自动机有什么区别？ 答案 米利机输出值 有限状态自动机不输出值

扩展：非确定性 在本节中，我们正在学习关于 确定性有限自动机。这意味着对于一个状态和一个有效输入，只有一个可能的转换可以执行。存在 非确定性有限自动机，其中对于给定的输入，可以执行多个路径（或没有路径） 在状态 p 中，对于输入 1，有两个可能的转换

状态转移表

一个 状态转移表 跟踪每个状态和输入。输入通常放在左侧，并与输出分开，输出放在右侧。以下是一个简单的示例，它包含一个具有两个状态的有限状态机和一个二进制输入

输入	当前状态	下一个状态	输出
0	S1	S2	null
1	S1	S1	null
0	S2	S1	null
1	S2	S3	null

练习：状态转移表 为以下 FSM 创建一个状态转移表 答案 输入 当前状态 下一个状态 输出 0 S1 S2 null 1 S1 S1 null 0 S2 S1 null 1 S2 S2 null 为以下 FSM 创建一个状态转移表 答案 输入 当前状态 下一个状态 输出 0 S0 S2 0 1 S0 S1 0 0 S1 S2 1 1 S1 S1 1 0 S2 S2 0 1 S2 S1 0 为以下状态转移表绘制 FSM 输入 当前状态 下一个状态 输出 计时器 绿色 绿色 null 按钮 绿色 黄色 null 计时器 黄色 红色 null 计时器 红色 绿色 null 答案 你可能已经注意到了。这代表一个交通灯系统 为以下状态转移表绘制 FSM 输入 当前状态 下一个状态 输出 a q0 q0 null b q0 q1 null a q1 q2 null b q1 q1 null a q2 q1 null b q2 q1 null 答案