数据表示基础:无符号二进制算术
您应该熟悉十进制中的加减乘法。计算机需要在二进制中执行相同的操作,您需要在考试中了解它!
让我们来看一个十进制加法的例子
25 +43 --- 68
这很简单,我们只需将每列加起来,但如果结果不能放入一列中会发生什么?我们需要使用进位位
98 +57 --- 155 11
希望您对这方面很熟悉。现在让我们看一下它如何在二进制中完成,并使用一个非常简单的例子,并在十进制中进行检查
01010 (1010) +00101 (510) ------ 01111 (1510)
这看起来非常简单,但当我们有进位位时会发生什么?与十进制中几乎相同
01011 (1110) +00001 (110) ------ 01100 (1210) 11

|
练习:二进制加法 1010 + 0001 答案 1010 +0001 ---- 1011 01001001 + 00110000 答案 01001001 +00110000 -------- 01111001 01010100 + 00110000 答案 01010100 +00110000 -------- 10000100 01001010 + 00011011 答案 01001010 +00011011 -------- 01100101 01111101 + 00011001 答案 01111101 +00011001 -------- 10010110 00011111 + 00011111 答案 00011111 +00011111 -------- 00111110 10101010 + 01110000 答案 10101010 +01110000 -------- 100011010 Note we have some overflow, this will come in useful when doing subtraction |
希望您在小学的时候已经学会了如何在十进制中将数字相乘。让我们回顾一下
12 x 4 -- 8 = 4*2 40 = 4*10–48
以及一个更复杂的例子
12 x14–8 = 4 * 2 40 = 4 * 10 20 = 10* 2 100 = 10* 10–168
二进制也是同样的原理。让我们来看一个例子
101 x 10 ---- 0 = 0 * 101 1010 = 10 * 101 [or in denary 2 * 5 = 10]
让我们尝试一个更复杂的例子
1011 [11] x 111 [7] ---- 1011 = 1 * 1011 10110 = 10 * 1011 101100 = 100 * 1011 ------ now add them together 1001101 = [77 double check with the decimal earlier]
|
练习:二进制乘法 101 * 10 答案 101 x 10 ---- 1010 11 * 11 答案 11 x 11 ---- 11 110 ---- 1001 1011 * 101 答案 1011 x 101 ------ 1011 101100 ------ 110111 1111 * 111 答案 1111 = 15
x 111 = 7
------
1111
11110
111100
------
1101001 = 105
如果将一个二进制数乘以 2,它会向左移动多少位? 答案 1 如果将一个二进制数乘以 16,它会向左移动多少位? 答案 4(因为 2^4 = 16) 这是计算机中乘法的快捷方式,它使用机器代码移位指令来执行此操作。不用担心,您不需要了解本课程大纲的这些内容 |
|
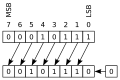
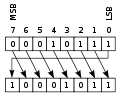
扩展:位移位 如果您查看以下数字的二进制表示,您可能会注意到一些奇怪的事情 0001 = 1 0010 = 2 0100 = 4 1000 = 8 每次我们将数字向左移动一位时,数字的值就会加倍。这不仅适用于一位,请查看这个更复杂的例子。 0001 0101 = 21 0010 1010 = 42 同样,向左移动一位,数字就加倍。另一方面,向右移动一位会将值减半。 计算机在进行乘法和除法方面 notoriously 糟糕,它需要大量的 CPU 时间,并且会严重降低代码速度。为了解决这个问题,计算机可以在寄存器中移动值,只要乘法或除法是 2 的幂,那么 CPU 时间就会减少,因为操作只需要一行机器代码。处理器可以执行几种类型的 移位
向左或向右移动,您会在空的一端添加一个 0。
您将保持被移动数字的符号位。 请注意,逻辑移位示例也是算术移位示例,因为符号保持不变。您将在学习补码时了解符号位
被推到一端的位出现在另一端
|