A-level 数学/MEI/D1/图

离散数学中的图与连续数学中的图略有不同。在连续数学中，图用于可视化两个变量之间的映射（例如 y=x²）。在离散数学中，图描述了对象之间的关系，这些对象被称为顶点或节点，这些对象通过边连接。边可以是无向的或有向的，如果它们是有向的，则使用箭头来指示边的遍历方向。由顶点和边连接而成的图被称为图。

可以使用以下集合推导从两个集合创建顶点对（如果您不熟悉集合推导，该表达式表示从两个集合：X 和 Y 中，生成每对可能的排列）。 $X\times Y=\{(x,y)|x\in X,y\in Y\}$

例子

$X=\{London,Cambridge,Birmingham\}$
$X\times X=\{(London,London),(London,Cambridge),(London,Birmingham),$
$(Cambridge,London),(Cambridge,Cambridge),(Cambridge,Birmingham),$ $(Birmingham,London),(Birmingham,Cambridge),(Birmingham,Birmingham)\}$

术语表

基本定义

图: 由对象组成的图，其中一些对象通过边连接。相互连接的对象称为顶点或节点，连接节点的链接称为边。
顶点/节点的度数/阶数: 连接到该顶点/节点的边的数量。
回路: 当一条边的末端是下一条边的起点并且没有顶点重复时形成的闭合路径。
有向边: 与方向相关的边，这用箭头表示边的遍历方向。
自环: 两端都具有相同顶点的边。
有向图: 有向图，至少有一条边与方向相关的图。

以下定义按普遍性排序，通路是最通用的，而哈密顿回路是最不通用的。

通路: 一系列边，其中一条边的末端是下一条边的起点。如果最后一条边连接到第一条边，则通路是闭合的，如果它没有连接，则通路是开放的。
轨迹: 没有边重复的通路。
路径: 没有顶点重复的轨迹。
回路: 最后一条边的末端连接到第一条边的图。
哈密顿回路: 恰好访问每个顶点一次的回路。

图的类型

连通图: 每对顶点之间都存在路径的图。
简单图: 没有自环且任意一对边之间不超过一条边的图。
完全图: 每对顶点之间都由一条边连接的简单图。
平面图: 可以不交叉任何一对边的图。
二分图: 由两组顶点组成的图，每条边连接一组中的一个顶点和另一组中的一个顶点。
有向图: 包含有向边的图。
树: 没有回路的简单连通图。

图的例子

这些例子是OCR MEI 能力规范中列出的例子，因此，在参加考试之前充分理解它们是明智的。

哥尼斯堡七桥问题

据说，在柯尼斯堡不可能不重复走过任何一座桥的情况下走完七座桥。欧拉研究了这个问题，将其转化为图论，并证明了 *任何具有奇数个顶点的图都不能被遍历*。

这个问题被转化为一个图，将桥视为边，将陆地视为节点。这种抽象掉无关细节的做法使欧拉能够专注于问题的核心属性，是建模任何问题的基本方面。

欧拉推断，当通过一座桥（边）进入一块陆地（节点）时，会通过另一座桥离开该陆地，因此进入一个节点的次数与离开该节点的次数相同，因此穿过陆地的桥的数量必须是偶数（前提是该节点 *不是* 起点或终点，在这种情况下，进入的次数是奇数）。由此得出，每个陆地（除选择作为起点和终点的陆地外）必须有偶数座桥（边）。问题中的所有四个陆地都与奇数座桥相连，最多只有 2 块陆地可以作为步行路线的起点/终点，因此桥梁不可能在一次步行中只走一次。

更正式地说
欧拉推断，当通过一条边进入非终点（非起点/终点）节点时，会通过另一条边离开该节点，因此进入该节点的次数

欧拉路径是一种遍历所有边一次的路径，起点和终点可以相同或不同。如果起点和终点相同，则该路径被称为欧拉回路。对于一个图来说，要想有一个欧拉回路，必须有零个奇数度节点，而欧拉路径可以有零个或两个奇数度节点。任何可以通过一次不抬起笔从纸上描绘所有边并且回到起点的图被称为 *欧拉图* 或 *可遍历图*。

过河

立方体塔

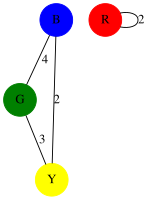
有四个立方体，每个立方体都有四个不同的颜色在其面上。这个谜题的目标是将这些立方体堆叠在一起形成一个 4x1x1 的长方体，这样长方体的每个面上都有四种不同的颜色。立方体的涂色如下：

立方体 1	立方体 2	立方体 3	立方体 4
蓝色对面是绿色	B 对面 G	R 对面 B	Y 对面 R
红色对面是红色	G 对面 R	R 对面 Y	Y 对面 G
黄色对面是蓝色	B 对面 Y	G 对面 Y	B 对面 G