A-level 数学/OCR/D1/节点图/介绍
本节讨论节点图,有时也称为图或网络。
首先,我们必须说明我们对图的理解。一个图是由点(我们称之为节点或顶点)和连接这些点的线(弧或边)组成的集合。在思考图时,每条弧的长度和布局并不重要,重要的是哪些顶点连接到哪些其他顶点。
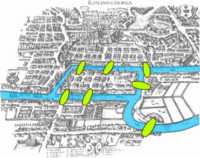
哥尼斯堡七桥问题,或称哥尼斯堡桥问题,是一个经典问题,是图论中的第一个问题之一。它是由普鲁士哥尼斯堡(今俄罗斯加里宁格勒)这座城市的实际布局引发的。
上面是这座城市的示意图,河流用蓝色表示,桥梁用绿色表示。问题是,是否有可能从城市中的某个地方出发,穿过每座桥一次且仅一次,并回到起点。数学家莱昂哈德·欧拉(1707-1783)设法解决了这个问题,他专注于重要的方面。他意识到,重要的是哪些地方相连,以及相连多少次,而不是每座桥的长度或布局。换句话说,这个问题可以用图来表示。下面是一个这样的表示
在这个图中,红色的点是顶点,代表河流的每条岸以及中间的两个岛屿。它们之间的线和曲线是弧,代表桥梁。欧拉对这个问题的解决方案在这个抽象的表示中更容易理解。他发现不可能只走一次就遍历每座桥,原因如下
当行人穿过桥梁时,他们在访问的每个地方(除了起点和终点之外)必须成对进出。也就是说,如果他们访问一次,他们就进入,然后离开,如果两次,他们就进入两次,离开两次,依此类推。这意味着,由于每次进出都必须经过不同的桥梁,而且所有桥梁都必须使用,因此除了路线的起点和终点之外,从每个点出发的桥梁数量必须是偶数。起点和终点一般来说可以是例外,因为行人从一个地方离开而不进入,进入另一个地方而不离开,所以从它们那里出发的桥梁数量将是奇数。但是,如果起点和终点相同,如这里要求的那样,那么进出就会再次配对,因此所有点都必须有偶数个桥梁从它们那里出发。
概括地说,如果每个点都有偶数个桥梁,那么这样的路线就是可能的。这意味着在哥尼斯堡七桥问题的情况下,不可能按顺序遍历每座桥一次且仅一次,因为每个点都有奇数个桥梁从它出发。即使从不同的地点开始和结束也不可能。
欧拉对哥尼斯堡七桥问题的解决方法得出了一个适用于所有图的结果。然而,在我们看到这个结果之前,我们需要一些更多的术语。
首先,欧拉路径是在图中从一个顶点到另一个顶点的路线,使用图中的所有边。欧拉回路是一条欧拉路径,其中起点和终点相同。这相当于这个问题中要求的。根据这些术语,如果存在欧拉回路,则图是欧拉图,如果存在欧拉路径但不是回路,则图是半欧拉图。最后,顶点的度数是从它出发的边的数量。
上面的结果表明,一个图只有当所有顶点的度数都是偶数时,才是欧拉图。换句话说,每个顶点的度数必须是偶数。后来证明,任何所有顶点的度数都是偶数的图都是欧拉图。类似地,当且仅当一个图只有 2 个顶点的度数是奇数时,它才是半欧拉图。
下面是一些图的示例,这些示例说明了如何判断一个图是欧拉图还是半欧拉图
-
示例一
-
示例二
-
示例三
-
示例四
示例一是一个既不是欧拉图也不是半欧拉图的图,因为有四个顶点的度数是奇数,而不是要求的零(对于欧拉图)或两个(对于半欧拉图)。
示例二和示例三是半欧拉图,因为只有两个顶点的度数是奇数。
示例四是欧拉图,因为所有顶点的度数都是偶数。
现在我们知道如何判断欧拉路径或回路是否存在。然而,我们还没有一个生成这种路径的方法。弗勒里算法是一种保证在存在欧拉路径或回路时提供这种路径或回路的方法。该方法如下
- 选择任何度数为奇数的顶点。如果没有,则选择任何顶点。
- 从该顶点选择任何一条边,我们可以从图中删除它而不使其断开连接。换句话说,当我们删除这条边时,我们仍然可以从任何顶点到达任何其他顶点。
- 穿过这条边,并将其从图中删除。
- 删除任何没有从它们出发的边的顶点。
- 如果还有边要穿过,则返回步骤 2。
如果我们遵循这种方法,我们将会遵循一条欧拉路径或试验,前提是存在一条欧拉路径。保持图连接的条件消除了我们将图分成两个“岛屿”的可能性,最终被困在一个岛屿上,没有未使用的边可以回到另一个岛屿。我们可以留下“孤立的”顶点,没有从它们出发的边,因为没有边可以从它们出发或到达它们进行遍历。这就是为什么我们可以删除它们的原因。
没有欧拉路径会像描述的那样分割图,所以任何欧拉路径都必须通过使用该算法来形成。
可能需要在此处定义更多术语。