A-level 数学/OCR/D1/节点图/生成树
在本模块中,我们将介绍生成树的概念,最小生成树,以及找到最小生成树的一些方法。
首先,我们必须说明我们所说的树是什么意思。树是一个图,其中任意一对顶点之间只有一条路径。这意味着树是连通的,即每对点之间至少存在一条路径。
树是连接一组顶点的最有效方式,从某种意义上说,如果我们有一棵树,那么每条边都是必要的,因为如果我们移除任何边,那么图就不再是连通的。此外,所有具有 n 个顶点的图上的树都恰好有 n - 1 条边。
如果我们有一个连通图 G,那么另一个图 H 是 G 的生成树,如果它是与 G 具有相同顶点的树,并且 H 的所有边都是 G 的边。
最后,我们将介绍最小生成树的概念。为了使这有意义,我们必须考虑称为网络的图。网络是图,其中每条边都有一个权重。权重可以是边的长度,或两点之间的距离,或者可以表示两点之间移动的难度,或者成本。在任何情况下,权重都是一个数字。它通常是正的(或非负的,零是可能的),但如果我们允许负数,数学原理也是相同的。由于图的每条边都被分配了一个距离,而不是顶点对本身,因此没有为没有边连接的顶点对分配距离。
给定一个图 G,其边分配有距离,那么最小生成树 H 是 G 的生成树,其中边的权重之和尽可能低。可能存在多个最小生成树。举一个简单的例子,任何具有所有权重为 1 的图 G 的生成树都将是一个最小生成树,相关总和等于 n-1,其中 n 是原始图的顶点数。
克鲁斯卡尔算法是为网络 G 寻找最小生成树的一种方法。我们从一个由 G 的所有顶点组成的图 H 开始,但没有边。然后我们按照以下说明进行
- 考虑 G 中的边集 E,这些边在添加到 H 时将连接端点
- 找到 E 中权重最低的成员。如果有多个这样的成员,选择任意一个。
- 将此边添加到 H 中
- 如果 H 未连接,则返回步骤 1。否则,H 是 G 的最小生成树。

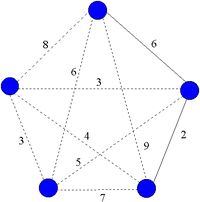
上面是图的图 (图 1),将使用克鲁斯卡尔算法为其构建生成树。每条边都给出了权重。这些线是点状的,因为生成树的边将用实线表示。
下面是图 2 到 5,它们指示生成树构建的阶段。




在图 2 中,我们添加了一条权重为 2 的边,因为它是权重最低的边。对于图 3,有两个选项,权重均为 3,可以添加。请注意,添加的边未连接到第一条边。在该算法下允许这样做,但在下面描述的普里姆算法下不允许这样做。在图 4 中,添加了另一个权重为 3 的边。最后,在图 5 中,我们添加了一条权重为 6 的边,其中有两个允许的边。存在权重更低的边,例如权重为 4 的边,但它们都连接了我们已经连接的边。最终的生成树在下面的图 6 中给出,原始图中的其他边及其权重未给出。总权重为 2+3+3+6 = 14。

普里姆算法是为网络 G 寻找最小生成树的另一种方法。我们再次从一个由 G 的所有顶点组成的图 H 开始,但没有边。然后我们按照以下说明进行
- 在图中选择任意顶点 v
- 使其成为集合 S 的唯一成员
- 考虑连接 S 的一个成员到不在 S 中的顶点的边集 E。
- 找到 E 中权重最低的成员。如果有多个这样的成员,选择任意一个。
- 将此边添加到 H 中,并将不在 S 中的顶点添加到 S 中。
- 如果 H 未连接,则返回步骤 3。否则,H 是 G 的最小生成树。

上面是图 7,它与图 1 相同,是用于克鲁斯卡尔算法示例的图。我们将构建一个不同的生成树,尽管可以保证总权重将相同。第一步是选择一个顶点作为起点。这将是最上面的顶点。下面是图 8 到 11,生成树构建的阶段。



在开始时,只有最上面的顶点在 S 中。S 与其他顶点之间权重最低的边是那些权重为 6 的边,因此在图 8 中选择了一个边,从而将中间右边的顶点添加到 S 中。在图 9 中,添加了权重为 2 的边,将右下方的顶点添加到 S 中。在图 10 中,添加了一个权重为 3 的边,另一个边在两端都没有 S 中的顶点。然后在图 11 中添加了此边。现在允许这样做,因为中间左边的顶点在图 10 中被添加到 S 中。最终的生成树在下面的图 12 中给出。总权重再次为 2+3+3+6=14,尽管实际的生成树与克鲁斯卡尔算法不同。

当我们感兴趣的图是矩阵形式时,找到最小生成树的另一种方法。在这种情况下,矩阵只是一个数字表,这些数字对应于边的权重。例如,下面是表 1,是我们一直在示例中使用的图的矩阵形式,以及图 13,熟悉的图形表示
|
 |
这些顶点被赋予 1 到 5 的数字,其中 1 是最上面的顶点,2 和 3 是中间左侧和中间右侧的顶点,而 4 和 5 是左下和右下方的顶点。行和列标题对应于这些数字,其他数字是相应边的权重。例如,第 1 行第 2 列中的数字 8 是顶点 2 和 3 之间边的权重 8。请注意,矩阵中存在对称性,例如第 2 行第 1 列也是 8。这是因为例如,顶点 1 和 2 之间的边也是顶点 2 和 1 之间的边。此外,顶点与自身之间没有边,因此第 1 行第 1 列、第 2 行第 2 列等都是空的。
使用这种形式,我们可以应用普里姆算法来找到最小生成树。我们将从顶点 4 开始,使其成为 S 的唯一成员。为了表示这一点,我们将它加粗,以后也会对 S 的其他成员进行加粗。你可以使用任何你想要的方法来表示 S 的成员,例如画圈。下面是表 2,其中顶点 4 被标记为 S 的成员。
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 8 | 6 | 6 | 9 | |
| 2 | 8 | 3 | 3 | 4 | |
| 3 | 6 | 3 | 5 | 2 | |
| 4 | 6 | 3 | 5 | 7 | |
| 5 | 9 | 4 | 2 | 7 |
现在,我们必须选择下一条边。它将有一个顶点在 S 中,一个顶点不在 S 中。这些对应于第 4 行(加粗的)中的数字,它不与第 4 列(也加粗的)交叉。这给出了数字 6、3、5 和 7,其中最小的是 3,对应于第 4 行第 2 列,因此是顶点 4 和 2 之间的边。因此,我们将此添加到我们的树中,并将 2 添加到 S 中。下面是表 3,其中 2 和 4(S 的成员)都加粗了。
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 8 | 6 | 6 | 9 | |
| 2 | 8 | 3 | 3 | 4 | |
| 3 | 6 | 3 | 5 | 2 | |
| 4 | 6 | 3 | 5 | 7 | |
| 5 | 9 | 4 | 2 | 7 |
现在,要选择的边对应于第 2 行和第 4 行(加粗的)中的数字,但不对应于第 2 列和第 4 列中的数字。这给出了数字 8、3、4、6、5 和 7。最小的是 3,对应于顶点 2 和 3 之间的边。因此,我们将 3 添加到 S 中,并将此边添加到我们的树中。下面是表 4,其中 3 现在加粗了。
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 8 | 6 | 6 | 9 | |
| 2 | 8 | 3 | 3 | 4 | |
| 3 | 6 | 3 | 5 | 2 | |
| 4 | 6 | 3 | 5 | 7 | |
| 5 | 9 | 4 | 2 | 7 |
现在,我们有数字 8、4、6、2、5 和 7。最小的是 2,对应于顶点 3 到 5 之间的边。因此,我们将此边添加到我们的树中,并将顶点 5 添加到 S 中。在表 5 中,此顶点被添加到 S 中,因此加粗了。
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 8 | 6 | 6 | 9 | |
| 2 | 8 | 3 | 3 | 4 | |
| 3 | 6 | 3 | 5 | 2 | |
| 4 | 6 | 3 | 5 | 7 | |
| 5 | 9 | 4 | 2 | 7 |
这里,数字分别是 8、6、6 和 9。因此,有两个可能的边,分别是 1 与 3 或 4 之间的边。之前的边分别为 4 与 2、2 与 3 以及 3 与 5 之间的边。以下是图 14 和 15,它们分别显示了选择其中一条边形成的生成树。图 14 中的边连接了顶点 1 和 3,而图 15 中的边连接了顶点 1 和 4。


注意,这些分别是普里姆算法和克鲁斯卡尔算法生成的生成树。还要注意,在寻找最小数字时,我们只考虑了 S 的成员是行,非成员是列的情况。这样就忽略了 S 的成员是列,非成员是行的可能性。然而,正如我们之前讨论的那样,每条边都会列出两次,而我们考虑元素的方式只包含每条边一次。例如,如果 1 在 S 中,而 2 不在 S 中,那么我们将它们之间的边包含在第 1 行第 2 列,但不包含在第 2 行第 1 列。
