A-level 物理 (进阶物理学)/圆周运动

展示圆周运动中关键变量的示意图。

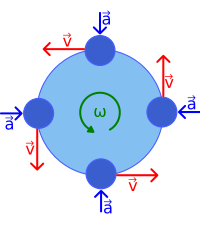
很少情况下，物体以圆周运动。一些行星以近似圆形轨道运行。绳子上的弹珠可能会绕着我的头部以圆形运动。汽车转弯时可能短暂地沿圆弧运动。关于圆周运动的关键点是，没有向外拉离圆周的力，也没有使运动物体沿着圆周切线方向运动的力。离心力不存在。圆周运动中只有一种力，称为向心力。它总是指向圆心。物体不会因为两力平衡而沿着圆周运动。相反，向心力以恒定大小，不断变化的方向，加速物体。物体具有速度，并且将继续以该速度运动，除非受到向心力的作用，向心力不断地向圆心增加速度。

如果你使静止的物体受到向心力的作用，它只会落下。如果你给它一点点速度，它仍然会落下，但它不会落在其起始位置的正下方。如果你不断增加速度并放下它，就会出现一个点，它会落在无限远处 - 它会进入轨道。这种“魔法”速度与向心力大小之间的关系如下所示：

$F={\frac {mv^{2}}{r}}$,

其中m是圆周运动物体的质量，v是其速度的大小，r是圆心到物体的距离。由于F=ma，向心加速度为：

$a={\frac {v^{2}}{r}}$

向心力可能表现为多种形式：绳子的张力、摩擦力、重力，甚至电场或磁场。在所有这些情况下，我们可以将向心力的方程与它实际代表的力的方程等效。

角速度

速度是位移变化率。角速度是角度变化率，通常用ω表示，以弧度/秒为单位测量。

$\omega ={\frac {\Delta \theta }{\Delta t}}$

在圆周运动中

$\omega ={\frac {2\pi }{T}}=2\pi f$,

其中T是一次旋转的时间，f是旋转频率。然而

$v={\frac {2\pi r}{T}}$

${\frac {v}{r}}={\frac {2\pi }{T}}$

因此，速度与角速度之间的关系是：

$\omega ={\frac {v}{r}}$

如果我们将此代入向心加速度的公式中

$a={\frac {(\omega r)^{2}}{r}}={\frac {\omega ^{2}r^{2}}{r}}=\omega ^{2}r$

问题

1. 一个质量为10克的网球被系在0.75米长的绳子上，以1.5赫兹的频率绕着某人的头部以圆周运动。绳子上的张力是多少？

2. 一颗行星绕一颗恒星以圆周运动。它的年为100个地球年，恒星到行星的距离为70吉米。恒星的质量是多少？

3. 一辆2000千克的汽车以20千米/时的速度转弯，转弯是圆弧的一部分。由于摩擦引起的向心力是汽车重量的1.5倍。弯道的半径是多少？

4. 利用向心加速度和引力场强度的公式，以及角速度的定义，推导出一个将行星的轨道周期与其轨道半径联系起来的方程。5. 一颗质量为1.5克的行星以0.5厘米的半径，以2赫兹的频率绕地球旋转。求力。

解答