A-level 物理 (进阶物理)/图

有两种类型的运动图，你需要能够使用和理解：距离-时间图和速度-时间图。

距离-时间图

一个物体以恒定速度运动 6 秒，停止 5 秒，然后在接下来的 7 秒内返回到其初始位置，在返回旅程的中间部分移动得更慢。

距离-时间图绘制物体离开某一点的距离，以时间为横轴，距离为纵轴。你需要能够使用和理解几种类型的运动图：距离-时间图、位置-时间图和速度-时间图。

位置-时间图或位移-时间图

距离-时间图可以告诉你速度，但速度永远不会是负数，所以距离-时间图中只能有正斜率。位置-时间图显示位移，有方向，你可以从中计算速度。如果我们把位置-时间图上的直线想象成一个函数 f(t)，给出 s = f(t) 的方程，我们可以对其进行微分，得到

${\frac {ds}{dt}}=f'(t)$,

其中 s 是位移，t 是时间。通过在任何给定的时间 t 找到 f'(t)，我们可以找到距离相对于 t 的变化率。这就是直线的斜率。正斜率意味着距离在增加，负斜率意味着距离在减少。斜率为 0 意味着物体静止。物体的速度是其位移的变化率，这与距离-时间图上直线的斜率相同。但这不一定与物体的平均速度 v 相同

$v={\frac {s}{t}}$

在这里，t 和 s 是特定时间段内位移和时间的总变化 - 它们不能告诉你任何给定时间点到底发生了什么。

速度-时间图

一个物体加速 6 秒，撞到某个物体，加速 5 秒，然后在剩下的 6.5 秒旅程中减速到停止。

速度-时间图绘制物体相对于某一点的速度，以时间为横轴，速度为纵轴。我们已经知道速度是距离函数的斜率（导数）。由于积分是微分的逆过程，如果我们有速度-时间图，并且想要知道物体在两个时间点之间的距离，我们可以找到这两个时间点之间图下的面积。一般来说

如果 $v=f(t)\,$

$s=\int _{t_{1}}^{t_{2}}f(t)\,dt$

其中 v 是速度（单位为 ms⁻¹），t 是时间（单位为 s），s 是物体在两个时间点 t₁ 和 t₂ 之间的距离（单位为 m）。

此外，通过微分，我们知道 v = f(t) 的斜率（或导数）等于物体在任何给定时间点的加速度（单位为 ms⁻²），因为

$a={\frac {dv}{dt}}$

问题

1. 在以下距离-时间图中，物体运动开始后 4 秒的速度是多少？

2a) 描述这个人的运动。

2b) 12 秒时的速度是多少？

3. 在以下速度-时间图中，物体在 7 秒到 9 秒之间运动了多少距离？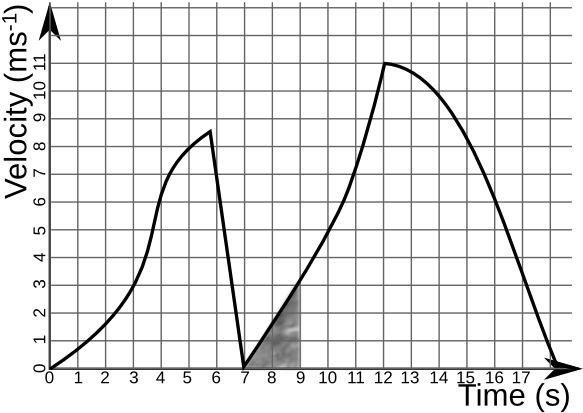

4. 物体在 8 秒时的加速度是多少？

5. 一辆汽车以 10ms⁻¹ 的速度在直线上行驶 5 分钟，然后在接下来的 4 分钟内以恒定速度返回其初始位置。绘制一张距离-时间图，显示汽车从其初始位置行驶的距离。

6. 绘制上述情况的速度-时间图。

以下问题比你将要遇到的任何问题都更难，但还是试一试吧

7. 小球的速度与它被抛出后的时间有关，方程为 $v=30-9.8t\,$。小球在 2 秒后运动了多远？

解答