高级无机化学/对称元素

高级无机化学/对称元素 (1.1)

对称元素是指分子中的几何实体：空间中一个假想的点、轴或平面，进行对称操作：旋转、反射或反转。^[1],[2] 对称元素的识别可以将对称性应用于分子性质，并可用于预测或解释分子的许多化学性质。对称元素和对称操作是群论中的两个基本概念，群论是对描述分子结构、键合和光谱的对称特性的数学描述。

内容

  1. Point of symmetry operations
     1.1. Identity, E
     1.2. Proper Rotation, Cn
     1.3. Reflection, σ
     1.4. Inversion, i
     1.5. Improper Rotation, Sn
  2. Point groups 
  3. Example: symmetry of benzene

1. 点对称操作
当一个分子至少存在一个点，在进行任何对称操作后仍然与原始分子无法区分时，就存在该分子的点对称。换句话说，如果且仅当新的排列的分子与原始排列无法区分时，旋转、反射或反转操作称为对称操作。一个分子可以拥有五种点对称元素，因此也有五种点对称操作。一个分子中所有的对称元素必须至少共有一个点，这个点位于分子的中心。

1.1. 恒等操作，E
恒等操作来自德语“Einheit”，意为“统一”。这个对称元素表示没有变化。所有的分子都有这个元素。

• 
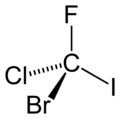
  图 1. CFClBrI。手性分子没有对称性，但有恒等操作 E。

1.2. 适当旋转，C_n
适当旋转操作相对于一个称为对称轴（也称为n倍旋转轴）的轴进行。一个轴，绕其旋转 360°/n（或 2π/n）后，旋转前后分子保持一致。n 值最高的轴称为主轴。

• 
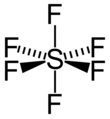
  图 2. SF₆ 的八面体结构。SF₆ 的适当旋转是 5C₂、4C₃ 和 3C₄，我们称 C₄ 为 SF₆ 的主轴。

一般来说，一个分子包含 nC_n 个操作，使得 {C_n¹, C_n², C_n³,…, C_n^n-1, C_nⁿ}，其中 C_nⁿ = E。例如，如果存在 C₅ 轴，那么存在 5C₅ (2C₅¹, 2C₅², C₅⁵) 个操作

• C₅¹ = C₅⁴，因为操作分别在顺时针和逆时针方向得到无法区分的分子。
• C₅² = C₅³，因为操作分别在顺时针和逆时针方向得到无法区分的分子。
• C₅⁵ = E

1.3. 反射，σ
反射操作相对于一个称为对称平面（也称为镜面）的平面进行。镜面有三种类型

• σ_h – 分子的水平镜面垂直于分子主轴。
• σ_v – 分子的垂直镜面包含分子主轴并穿过键（原子）。
• σ_d – 分子的二面角（也称为对角镜面）包含分子主轴，同时平分与之垂直的两个 C₂ 轴之间的角度。因此，ơ_d 不穿过键（原子）。

注意：σ_d 是 σ_v 的特例。

• 
  图 3. H₂O 的弯曲结构。水分子沿 C₂ 轴有两个 σ_v，没有 σ_h。

1.4. 反转，i
反转操作相对于一个称为对称中心（也称为反转中心）的点进行。它与绕 C₂ 轴旋转一个分子，然后将其反射到垂直于 C₂ 的镜面的结果相同。例如，图 2 中的 SF₆ 在中心 S 处有一个反转点。

1.5. 不适当旋转，S_n
不适当旋转操作相对于一个称为旋转-反射轴的轴进行。换句话说，它是绕轴旋转 360°/n（或 2π/n）然后在垂直于旋转轴的平面上反射的组合操作。

• 
  图 4. 交错茂金属 (左) 有 S₁₀ 操作，而重叠茂金属 (右) 有 S₅ 操作。

2. 点群
一个分子的所有对称元素的完整集合构成一个数学群的基础，而通过某种规则相互关联的对称操作集合被称为点群

• 封闭性 – 如果两个对称操作位于同一个群中，那么它们的乘积，导致另一个操作，也将位于同一个群中
  

                                    If A∈G and B∈G, then (A∩B)∈G

• 结合律 – 结合律适用于所有对称操作
  

                                          (AB)C=A(BC)

• 恒等式 – 存在一个与其他操作交换的（恒等式，E）并且不改变其他操作的操作
  

                                      If A∈G and E∈G, then AE=EA=A

• 逆元 – 对于群中的每个对称操作，都存在一个逆操作，它们的乘积导致恒等式
  

                       If A∈G, then there exists A-1∈G such that AA-1=A-1A=E

有关对称特性的数学表示的更多信息，另请参见

• 分子点群 (1.2)
• 矩阵 (1.3)
• 表示 (1.4)
  

在高级无机化学中。

3. 例子：苯的对称性
苯是具有多种对称元素和对称操作的分子之一。

• 

4. 参考文献
[1] Pfenning, Brian W. (2015). 无机化学原理. 霍博肯：John Wiley & Sons, Inc.. pp. 195.
[2] https://www-e.openu.ac.il/symmetry/symmetry-tutorial.html