模拟电子学/电流镜/Wilson

模拟电子学

Wilson 电流镜

Wilson 电流镜，以发明这种电路的工程师 George Wilson 命名，被广泛认为是解决简单 BJT 电流镜的有限 β 误差的巧妙且优雅的解决方案。

为了使其正常工作，需要满足以下条件

Q1 和 Q2 必须匹配，以便在相同的基极电流下，它们的集电极电流相等
所有三个晶体管具有相同的共射极电流增益 β

由于 Q1 和 Q2 具有相同的发射极电压（接地）和相同的基极电压（因为它们连接在一起），因此基极电流相同。我们将此电流称为 I_B

[W1]

I_{B1}=I_{B2}=I_{B}\,

从上面的条件 1，我们可以说 Q1 和 Q2 中的集电极电流是相同的（I_C）

[W2]

I_{C1}=I_{C2}=I_{C}\,

现在，从基本的 BJT 方程，我们知道 Q3 的基极电流由下式给出

[W3]

I_{B3}={\frac {I_{O}}{\beta }}

类似地，发射极电流也是已知的

[W4]

I_{E3}={\frac {\beta +1}{\beta }}I_{O}

从图和 KCL 可以明显看出，以下内容是正确的

[W5]

I_{E3}=I_{C2}+I_{B1}+I_{B2}\,

从方程 W1 和 W2 代入，我们得到

[W6]

I_{E3}=I_{C}+2I_{B}\,

鉴于 I_C=βI_B（条件 2 和基本的 BJT 方程），我们有

[W7]

I_{E3}=I_{C}+2{\frac {I_{C}}{\beta }}=I_{C}\left(1+{\frac {2}{\beta }}\right)=I_{C}\left({\frac {2+\beta }{\beta }}\right)

从方程 W4 代入 I_E3

[W8]

I_{O}\left({\frac {\beta +1}{\beta }}\right)=I_{C}\left({\frac {2+\beta }{\beta }}\right)

重新排列以使 I_C 成为主体，我们有

[W9]

I_{C}=I_{O}\left({\frac {\beta +1}{\beta +2}}\right)

现在，让我们考虑参考电流 I_REF。通过 KCL，然后从 W2 代入，

[W9]

I_{REF}=I_{C1}+I_{B3}=I_{C}+I_{B3}\,

从 W3 和 W9，我们现在有

[W10]

I_{REF}=I_{O}\left({\frac {\beta +1}{\beta +2}}\right)+{\frac {I_{O}}{\beta }}=I_{O}\left({\frac {\beta +1}{\beta +2}}+{\frac {1}{\beta }}\right)\,}

重新排列，

[W11]

I_{O}={\frac {I_{REF}}{\left({\frac {\beta +1}{\beta +2}}+{\frac {1}{\beta }}\right)}}

最后，通过简单的分数加法和因式分解进行简化，我们得到

[W12]

I_{O}={\frac {I_{REF}}{1+{\frac {2}{\beta \left(\beta +2\right)}}}}

很明显，如果 β 很大，那么 β(β+2) 很大，上面表达式中的分母接近 1，输出电流 I_O 接近参考电流 I_REF

[W13]

\lim \limits _{\beta \to \infty }\left({I_{O}}\right)=I_{REF}

然而，由于二次项的存在，即使 β 的值远低于简单的电流镜，也能获得非常好的近似值。例如，对于 β 值为 50 的晶体管，理论上可以预期电流偏差约为 0.75 μA。对于 β 值为 150，电流偏差降至 87 nA。

需要注意的是，威尔逊电流镜不是一个恒流源。如果电源电压 V_CC 发生变化，输出电流也会发生变化。假设参考电流 I_REF 由连接到电源电压的电阻提供。假设所有晶体管的 v_BE 为 0.7 V。现在，Q1 和 Q2 的基极电压为 0.7 V，因为发射极接地。因此，Q3 的基极电压为 (0.7+0.7)=1.4 V。这意味着参考电流由下式给出

[W14]

I_{REF}={\frac {V_{CC}-1.4}{R_{REF}}}

因此，输出电流也将取决于电源电压。将恒流源用作参考电流将确保输出电流恒定。

输出电阻

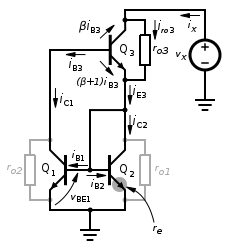
让我们考虑右侧的小信号模型。晶体管已被替换为小信号 T 型模型，然后被绘制成一个大信号 BJT，并行连接了小信号输出电阻 r_o。有关详细信息，请参见此处。Q1 和 Q2 中的输出电阻出现在此模型中，但它们被灰显，因为它们在分析中没有作用。参考电流在小信号模型中被禁用，这意味着 Q3 的基极仅连接到 Q1 的集电极。

我们将通过在输出端施加一个电压 v_x 并找出该电压与流过输出端的电流 i_x 之间的关系来找到电流镜的输出电阻 R_o。首先，请注意，基极电流流出Q3 的基极，因此 Q3 的集电极和发射极电流相反（这些电流仅出现在大信号 BJT 中，与 i_C3 和 i_E3 不同，尽管 i_B3 在两者中是相同的）。这只是为了从分析中去除负号。如果它们不相反，分析仍然会得到相同的结果。

首先，回想一下，Q1 和 Q2 是匹配的，因此集电极电流相同，基极电流也相同。我们把这些电流简称为 i。此外，Q1 的集电极电流等于 Q3 的（向外）基极电流。这导致了以下表达式

i_{C1}=i_{C2}=i_{B3}=i\,

从共发射极方程，我们也知道基极电流

i_{B1}=i_{B2}={\frac {i}{\beta }}

从共发射极方程，我们也可以给出大信号 BJT 在 Q3 中的集电极和发射极电流。这些电流如示意图所示。从 KCL，我们也可以证明，在 Q2 的集电极-基极连接处，

i_{E3}=i_{B1}+i_{B2}+i_{C2}={\frac {2i}{\beta }}+i

i_{E3}=i\left(1+{\frac {2}{\beta }}\right)

Q1 或 Q2 的基极-发射极电压 v_be1 由发射极中的（大信号）电流乘以大信号基极-发射极电阻给出，在 T 型模型中通常用 r_e 表示

v_{be1}=\left(\beta +1\right){\frac {i}{\beta }}r_{e}=i\left({\frac {\beta +1}{\beta }}\right)r_{e}

在 Q3 大信号集电极/输出电阻结点处的 KCL（密切注意电流方向）表明，Q3 输出电阻中的电流 i_ro3 由下式给出

i_{ro3}=i\left(1+{\frac {2}{\beta }}\right)+i\left(\beta +1\right)

i_{ro3}=i\left(\beta +2+{\frac {2}{\beta }}\right)

根据欧姆定律，我们可以计算出输出电阻上的电压

v_{ro3}=i\left(\beta +2+{\frac {2}{\beta }}\right)r_{o}

因此，电压 v_x 由该电压和 Q1 或 Q2 的基极-发射极电压之和给出

v_{x}=i\left({\frac {\beta +1}{\beta }}\right)r_{e}+i\left(\beta +2+{\frac {2}{\beta }}\right)r_{o}

电流 i_x 可以使用 Q3 输出电阻顶部的 KCL 找到

i_{x}=i_{ro3}-\beta i=i\left(2+{\frac {2}{\beta }}\right)

输出电阻 R_o 定义如下

R_{o}={\frac {v_{x}}{i_{x}}}

在消去 i 的因子后，得到一个有点凌乱的方程

R_{o}={\frac {\left({\frac {\beta +1}{\beta }}\right)r_{e}+\left(\beta +2+{\frac {2}{\beta }}\right)r_{o}}{2+{\frac {2}{\beta }}}}

现在，r_e 由方程 $r_{e}={\frac {\beta }{\beta +1}}{\frac {1}{g_{m}}}$ 给出。有关此内容的更多详细信息，请参见 T 型模型页面。请注意，涉及 β 的两个分数抵消，只剩下 ${\frac {1}{g_{m}}}$ 。由于 g_m 通常约为 20mS，因此该项约为 50Ω。考虑到这将添加到涉及 β（约为 100）乘以 r_o（约为 50kΩ）的项，因此该项无关紧要。现在，我们可以写出非常好的近似值，