人工神经网络/激活函数

激活函数

神经网络中使用了许多常见的激活函数。这不是一个详尽的列表。

阶跃函数

阶跃函数类似于原始感知器中使用的函数。如果输入和超过某个阈值，则输出为某个值 A₁；如果输入和低于某个阈值，则输出为 A₀。感知器中使用的值为 A₁ = 1 和 A₀ = 0。

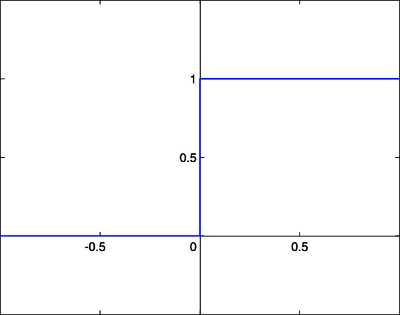
这些类型的阶跃激活函数对于二元分类方案很有用。换句话说，当我们想要将输入模式分类到两个组中的一个时，可以使用具有阶跃激活函数的二元分类器。另一个用途是创建一组小的特征识别器。每个识别器都是一个小的网络，如果存在特定的输入特征，则输出 1，否则输出 0。将多个特征检测器组合到一个网络中，可以解决非常复杂的聚类或分类问题。

线性组合

线性组合是指神经元的加权和输入加上线性相关的偏置成为系统输出。具体来说

$y=\zeta +b$

在这些情况下，输出的符号被认为等同于阶跃函数系统的 1 或 0，如果

$\theta =-b$.

连续Log-Sigmoid函数

Log-Sigmoid函数，也称为逻辑函数，由以下关系给出

$\sigma (t)={\frac {1}{1+e^{-\beta t}}}$

其中 β 是斜率参数。这被称为 log-sigmoid，因为也可以使用双曲正切函数而不是这种关系来构造 sigmoid，在这种情况下，它将被称为 tan-sigmoid。在这里，我们将 log-sigmoid 简称为“sigmoid”。sigmoid 具有类似于阶跃函数的特性，但增加了不确定区域。在这方面，sigmoid 函数非常类似于生物神经元的输入-输出关系，尽管并不完全相同。以下是 sigmoid 函数的图形。

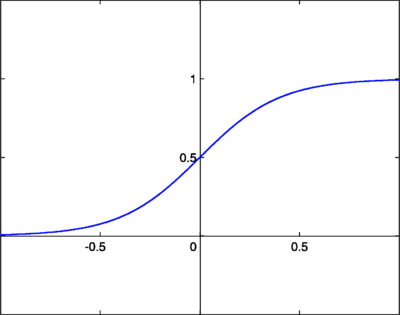
sigmoid 函数也很受欢迎，因为它们的导数很容易计算，这有助于在某些训练算法中计算权重更新。当$\beta =1$时的导数由下式给出

${\frac {d\sigma (t)}{dt}}=\sigma (t)[1-\sigma (t)]$

当$\beta \neq 1$时，使用$\sigma (\beta ,t)={\frac {1}{1+e^{-\beta t}}}$，导数由下式给出

${\frac {d\sigma (\beta ,t)}{dt}}=\beta [\sigma (\beta ,t)[1-\sigma (\beta ,t)]]$

连续Tan-Sigmoid函数

$\sigma (t)=\tanh(t)={\frac {e^{t}-e^{-t}}{e^{t}+e^{-t}}}$

其导数为

${\frac {\operatorname {d} \sigma (t)}{\operatorname {d} t}}=1-\tanh ^{2}(t)=\operatorname {sech} ^{2}(t)=1-{\frac {(e^{t}-e^{-t})^{2}}{(e^{t}+e^{-t})^{2}}}$

ReLU：线性整流函数

ReLU激活函数定义为

$\sigma (t)=\max(0,t)$

它也可以用分段函数表示

$\sigma (t)={\begin{cases}0&{\text{if }}t<0\\t&{\text{if }}t>0\end{cases}}$

ReLU激活函数

其导数为

$\sigma (t)={\begin{cases}0&{\text{if }}t<0\\1&{\text{if }}t>0\end{cases}}$

ReLU 最初由 Fukushima Kunihiko 于 1969 年为图像的表示学习引入，现在是深度学习中最流行的激活函数。它具有非常简单的公式和导数，使得反向传播计算更容易计算。由于导数函数的输出对于正输入始终为 1，因此与其他激活函数相比，它不太容易受到梯度消失或爆炸问题的影响。ReLU确实存在“死亡 ReLU”的独特问题，其中某些节点可能很少激活或“死亡”，无法为模型提供预测能力。为了避免死亡 ReLU 问题，引入了 Leaky ReLU 和 Parametric ReLU 等 ReLU 变体。

Softmax 函数

Softmax 激活函数主要在聚类系统的输出层中使用。Softmax 函数将原始值转换为后验概率。这提供了一种确定性度量。Softmax 激活函数表示为

$y_{i}={\frac {e^{\zeta _{i}}}{\sum _{j\in L}e^{\zeta _{j}}}}$

L 是输出层中神经元的集合。