汇编语言与计算机组成/引言和概述

本章介绍了计算机体系结构和计算机算术的基础知识。

计算机的功能

为了探究计算机如何运作，我们首先要弄清楚计算机究竟在做什么。毫无疑问，你对计算机的功能有所了解。毕竟，很可能你现在正在用电脑阅读这篇文章！如果我们试图列出计算机的所有功能，我们将得到一个惊人的复杂的功能和特性组合。相反，我们需要做的是剥开所有功能层，看看后台发生了什么。

基本计算机

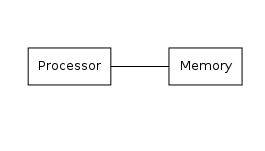
如果我们从最抽象的层面上看待一台计算机，它们所做的事情就是处理信息。我们可以将这种抽象的机器表示为某种存储器和某种处理器。处理器可以根据指令列表读取和写入存储器中的项目，而存储器只是记住它接收到的数据。处理器执行的指令列表被称为计算机程序。这种安排如何实现的细节决定了计算机本身的性质。使用这种定义，相当广泛的设备可以被归类为计算机。我们称之为“计算机”的大多数设备实际上都是通用计算机。也就是说，如果给它们无限的存储器，它们将能够计算任何可计算的函数。通用计算机的要求实际上非常简单。基本上，一台机器是通用的，如果它能够执行以下操作

1. 从内存中读取一个值。
2. 根据读取的值，确定一个新的值写入内存。
3. 根据读取的值，确定下一个要执行的指令。

遵循这些规则的机器被称为“图灵完备”。图灵完备的完整定义超出了本书的范围。如果你感兴趣，请参阅关于图灵机和图灵完备性的文章。

试图根据通用计算机的约束条件来创建程序将非常困难。创建更实用的指令列表会更方便，例如“加”、“减”、“乘”和“除”。处理器可以执行的指令列表被称为机器的指令集。该指令集有助于定义机器的行为，并进一步定义将在机器上运行的程序的性质。

机器的另一个决定性特征回答了“程序存储在哪里？”这个问题。你会注意到，在我们对基本计算机的图示中，我们没有显示程序位于何处。这样做是有目的的，因为回答这个问题有助于定义不同类型的计算机。进一步分解系统的组件是下一节的主题。

计算机体系结构

计算机的另一个决定性特征是系统的逻辑布局。这个属性被称为计算机的体系结构。计算机体系结构描述了机器如何逻辑组织以及它的指令集是如何实现的。设计计算机时，最重大的架构决策之一是如何组织它的内存，以及如何将程序加载到机器中。在计算机早期历史中，存储程序计算机和硬连线计算机之间存在区别。例如，第一台通用电子计算机 ENIAC 是通过将机器的单元连接到称为功能表的设备来编程的。后来的机器，如 EDSAC，将程序作为数据存储在程序内存中。当然，存储程序被证明更加方便。与简单地将新数据加载到机器中相比，重新连接一台机器需要的时间太长了。在当今的计算时代，几乎所有计算机都是存储程序计算机。在这本书中，我们将重点关注存储程序计算机体系结构。

确定了将程序作为数据存储后，我们现在必须将注意力转向程序在内存中存储的位置和方式。在过去，人们提出了许多不同的解决方案，但今天主要有两个高层变体。它们是冯·诺依曼体系结构和哈佛体系结构。

冯·诺依曼体系结构

冯·诺依曼体系结构是当今存在的最常见的体系结构。PC、Mac 甚至 Android 手机都是冯·诺依曼计算机的例子。

冯·诺依曼体系结构是一种存储程序计算机，它包含以下组件

1. 一个 CPU（中央处理单元），它执行程序指令。
2. 一个内存，它同时存储程序和数据。
3. 输入和输出设备

冯·诺依曼体系结构的决定性特征是数据和指令都存储在同一个内存设备中。程序被存储为 CPU 解码以执行指令的二进制模式集合。当然，数据也被存储为内存中的位模式。CPU 只能通过在内存中遇到数据的上下文来区分数据和程序代码。这种体系结构中的 CPU 从某个内存位置开始执行指令，并继续逐步执行指令。在遍历程序时遇到的任何内容都被视为程序指令。当 CPU 收到读取或写入内存数据的指令时，CPU 会将内存中的数字视为数据。当然，这也意味着冯·诺依曼机器完全能够修改自己的程序。

计算机算术

计算机花费大量时间计算简单的算术表达式。事实上，如果我们从“计算”的角度思考，算术就是首先想到的。因此，计算机如何处理数字是计算机体系结构研究的重要组成部分。第一台电子计算机 ENIAC 使用与人类相同的方式表示数字，使用十进制算术及其运算。这种方法的问题在于，你必须有 10 个可区分的状态（0 到 9），这大大增加了操作它的机器的复杂性。表示和区分 10 个状态需要非常精确的电子设备。如果我们想用电子设备制作简单的表示，最简单、最容易区分的是两个状态“开”和“关”。这不需要那么精确的检测和传播，因此它极大地简化了机器的物理实现，但是它确实引出了“如何用只有两个符号来进行数学运算？”的问题。

答案是我们使用二进制数系统，其中这些状态映射到 0 和 1。所以我们可以将 0 视为“关”，将 1 视为“开”。本节将解释这个数字系统是如何工作的，并介绍表示这些数字的方便方法。

数字的表示和基数

为了理解二进制，我们需要首先了解整数本身的性质。我们必须稍微深入一下数论的领域，但我保证它不会很痛苦！我们从一个简单的例子开始。你在下面看到了什么？

$145$

换句话说，你可能会说这是数字“一百四十五”。然而，这并不准确。你真正看到的是这个数量的表示。从小学开始，你就被教导了一种特定的写数字的方法。这个系统被称为“十进制”或“十进制”数系。当你看到“145”时，你实际上是在看到一种约定，其中

$145=1\cdot 100+4\cdot 10+5\cdot 1$

注意，这些项都是十的幂。因此我们可以将其改写为

$145=1\cdot 10^{2}+4\cdot 10^{1}+5\cdot 10^{0}$

口语化地说，我们称数字中的位置为“个位、十位和百位”。如果我们继续下去，每个位置的十的幂都比前一个位置大 1。因此我们可以构建一个表格，我相信你以前肯定见过。

${\begin{array}{|c|r|l|}\hline {\textrm {Exponent}}&{\textrm {Number}}&{\textrm {PlaceName}}\\\hline 10^{0}&1&{\textrm {Ones}}\\10^{1}&10&{\textrm {Tens}}\\10^{2}&100&{\textrm {Hundreds}}\\10^{3}&1,000&{\textrm {Thousands}}\\10^{4}&10,000&{\textrm {TenThousands}}\\10^{5}&100,000&{\textrm {HundredThousands}}\\\hline \end{array}}$

当然，我们可以通过简单地增加指数来无限地继续下去，添加新的位置值。我们可以用十进制系统推广这一点，说一个由$k$ 个数字组成的序列的值用一个多项式表示为

$\langle d_{k}\ldots d_{2}d_{1}d_{0}\rangle =\sum _{i=0}^{k}10^{i}$

注意，我们可以用任何任意的数字基数来表达这一点。因此，我们可以对上述内容进行推广，说对于一个任意的基数 $b$，一个由$k$ 个数字组成的序列的值是

$\langle d_{k}\ldots d_{2}d_{1}d_{0}\rangle =\sum _{i=0}^{k}b^{i}$

这为表示数字提供了许多可能性。你可以选择你喜欢的任何任意的基数。你使用的数值基数决定了用于表示数字的符号以及如何解释这些符号。一般来说，对于一个基数 $b$，我们必须有 $b$ 个符号来表示它。对于十进制，我们有 10 个符号 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)。注意，每个位置中使用的最高值符号的值是 $b-1$。因此，只要我们有一组符号来支持它，我们就可以使用任何我们选择的数字基数。

二进制数

现在我们可以将注意力转向与“开”和“关”两种易于识别的状态相匹配的数字基数。这就是二进制或以 2 为基数的数字系统。从上面的观察中，二进制数字系统只包含符号 (0, 1)。它的“位置”定义如下表所示

${\begin{array}{|c|r|l|}\hline {\textrm {Exponent}}&{\textrm {Number}}&{\textrm {PlaceName}}\\\hline 2^{0}&1&{\textrm {Ones}}\\2^{1}&2&{\textrm {Twos}}\\2^{2}&4&{\textrm {Fours}}\\2^{3}&8&{\textrm {Eights}}\\2^{4}&16&{\textrm {Sixteens}}\\2^{5}&32&{\textrm {Thirty-Twos}}\\2^{6}&64&{\textrm {Sixty-Fours}}\\2^{7}&128&{\textrm {OneHundredTwentyEights}}\\\hline \end{array}}$

就像十进制一样，我们可以通过简单地增加指数将此继续到无穷大。我在 8 位后停止了，因为正如我们将在后面看到的，这是我们在计算机中经常使用的单位。所以，假设我们有以下二进制数

$10010001$

我们如何确定它的值？请记住，这遵循与十进制数相同的规则，因此从左到右，我们可以将此数转换为十进制数，如下所示：

$1\cdot 128+0\cdot 64+0\cdot 32+1\cdot 16+0\cdot 8+0\cdot 4+0\cdot 2+1\cdot 1=145$

现在我们已经了解了如何将二进制（或任何进制数）转换为十进制，您可能想知道我们如何进行另一个方向的转换。也就是说，如何将十进制数转换为二进制（或任何任意进制）。答案很简单。我们可以通过反复除以目标进制来将十进制数转换为任何进制数。每个除法的余数从右到左表示转换后的数字的位数。证明为什么这有效留给读者作为练习。让我们通过将我们的好朋友 145 转换为二进制来测试一下。

${\begin{aligned}145\div 2&=&72~&R=1\\72\div 2&=&36~&R=0\\36\div 2&=&18~&R=0\\18\div 2&=&9~&R=0\\9\div 2&=&4~&R=1\\4\div 2&=&2~&R=0\\2\div 2&=&1~&R=0\\1\div 2&=&0~&R=1\\\end{aligned}}$

请注意，一旦商为 0，我们就可以停止，因为它将从这里开始一直保持为 0。因此，我们可以通过以相反的顺序读取余数来读取二进制数

$10010001$