天体力学/经典轨道要素

天体力学

轨道参数

可以使用一组 5 个参数完全指定轨道。利用这 5 个参数，我们可以精确地指定轨道的方位、在 3 维空间中的方向以及大小。如果我们有一个可选的第六个参数，我们可以确定卫星在任意时间 t 的轨道上的确切位置。这 6 个参数称为开普勒要素。

然而，在我们讨论这 6 个轨道参数之前，我们需要引入一些新的术语。

角动量

从地球中心指向卫星或感兴趣物体的向量称为 r，其速度向量称为 v。垂直于这两个向量的向量称为 比角动量 向量。

[角动量]

$\mathbf {h} =\mathbf {r} \times \mathbf {v}$

升交点

地球赤道位于一个称为 基本平面 的平面内（因为它位于地心-赤道坐标系中，我们将在本节中使用），而向量 r 所描绘的轨道形成一个称为 轨道平面 的平面，它包含向量 r 和 v。这两个平面的交线称为 节点线。

我们可以通过对角动量向量 h 和单位向量 K = <0, 0, 1> 取叉积来找到向量 n。

[升交点]

$\mathbf {n} =\mathbf {K} \times \mathbf {h}$

n 是节点线上指向 升交点 方向的向量。升交点是卫星以北方向穿过赤道的点。同样，降交点是卫星以南方向穿过赤道的点。

在赤道轨道中，n 未定义，并且没有节点。

顺行和逆行

顺行 或直接表示卫星绕地球从西向东运行。逆行 表示卫星从东向西运行。倾角在 0 到 90 度之间的物体以与主天体自转相同的方向绕其运行。倾角正好为 90 度的物体具有垂直轨道，既不是顺行也不是逆行。倾角在 90 度到 180 度之间的物体处于逆行轨道。

视觉表示

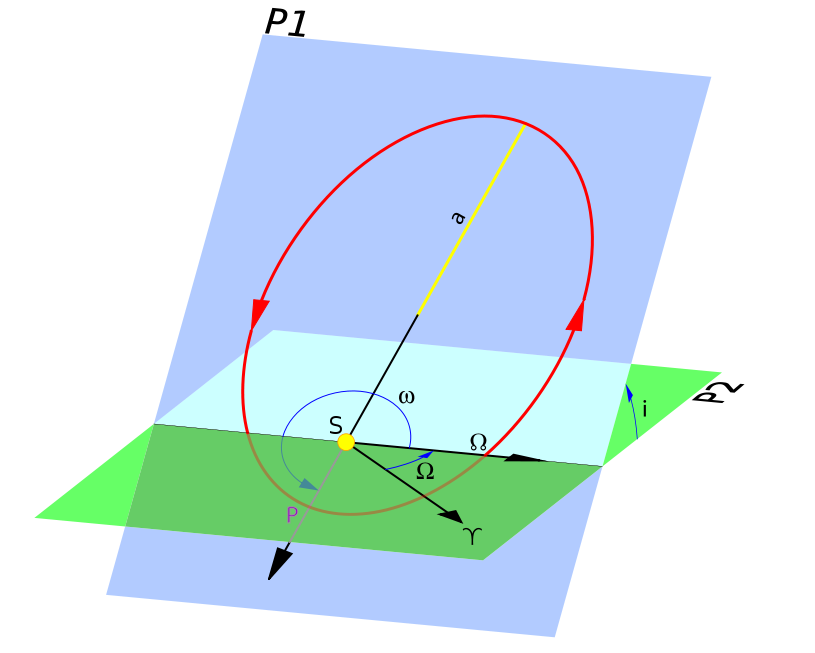
此图像显示了两个平面，轨道平面（淡黄色）和参考平面（灰色）。地球或主焦点被认为位于两个平面的中心的点。请注意，轨道如何在两个点处与黄道相交：一次是向北（升交点），一次是向南（降交点）。降交点在此图像中未标记，但其位置应该很明显。我们将在下面解释其他一些术语。

经典要素

现在我们有了节点向量，以及向量 r、v 和 h，我们可以找到我们的 5 个经典轨道要素。

半长轴

半长轴 a 可以通过 Vis-Viva 方程求得

$a=-{\frac {\mu }{2{\mathcal {E}}}}=-{\frac {\mu }{2}}\left[{\frac {v^{2}}{2}}-{\frac {\mu }{r}}\right]^{-1}$

其中一些术语仍然未定义。

偏心率

偏心率 e 可以通过偏心率向量的幅值确定

[偏心率向量]

$\mathbf {e} =\left({\frac {v^{2}}{\mu }}-{\frac {1}{r}}\right)\mathbf {r} -{\frac {\left(\mathbf {r} \cdot \mathbf {v} \right)}{\mu }}\mathbf {v}$

或者，它可以表示为

[偏心率]

$e={\sqrt {1+{\frac {2{\mathcal {E}}h^{2}}{\mu ^{2}}}}}$

尽管偏心率向量将在计算后续要素时需要。

倾角 ($i$)

倾角i是K单位向量与角动量向量h之间的夹角。它可以使用以下公式计算：

[轨道倾角]

$i=\arccos {\frac {h_{K}}{h}}$

倾角始终小于180°。

升交点赤经 ($\Omega$)

升交点赤经Ω是升交点与I单位向量之间的夹角。它可以计算为

[升交点赤经]

$\Omega =\arccos {\frac {n_{I}}{n}}$

如果n_J分量大于零，则Ω小于180°。否则，Ω大于180°。

近心点幅角 ($\omega$)

近心点幅角是轨道平面内升交点与近心点之间的夹角。我们可以计算它为

[近心点幅角]

$\omega =\arccos {\frac {\mathbf {n} \cdot \mathbf {e} }{ne}}$

如果e_K大于0，则ω小于180°。否则，ω大于180°。

近心点通过时间

近心点通过时间是卫星到达近心点的时间。我们将此时间定义为T_p。它可以从观测中确定。这是第六个轨道参数，它允许计算天体在任何时间的位置。

可选要素

近心点赤经 ($\Pi$)

近心点赤经是升交点赤经和近心点幅角之和

[近心点赤经]

$\Pi =\Omega +\omega$

历元真近点角 ($\nu _{0}$)

历元真近点角是从近心点到卫星在历元T₀处的半径向量的角度，表示为$\nu _{0}$

历元纬度幅角 ($u$)

历元纬度幅角是升交点与卫星在历元处的夹角

$u=\nu +\omega$

真经度在历元 ($l$)

真经度在历元是参考方向（通常是春分点 ♈）与卫星位置之间的角度。它从参考方向到升交点（如果存在）在参考平面测量，然后从升交点到卫星在轨道平面上的位置测量。

$l=\Omega +\omega +\nu =\Pi +\nu =\Omega +u$

寻找 r 和 v

从五个经典轨道要素，我们可以确定 r 和 v。

$\mathbf {r} =r\cos(\nu )\mathbf {P} +r\sin(\nu )\mathbf {Q}$

$\mathbf {v} ={\sqrt {\frac {\mu }{p}}}[-sin(\nu )\mathbf {P} +e\mathbf {Q} +\cos(\nu )\mathbf {Q} ]$

其中 P 和 Q 是近心坐标系中的单位向量。使用我们的坐标转换，我们可以将其转换为地心赤道坐标。