天体动力学/轨道面内变化

为了在太空中改变你的轨道,你必须首先确定你的航天器指向哪个方向。 “前进方向”或你正在移动的方向通常标记为“顺行”。相反的方向通常标记为“逆行”。
霍曼转移是在两个共面轨道之间进行的两次燃烧转移。在二体系统中,它几乎总是两个圆形轨道之间最有效的转移,就ΔV而言。
轨道转移可以是“近霍曼”,这意味着它们仍然有效,但不是最有效的。近霍曼转移轨道的一个例子是火星勘测轨道器转移轨道。
双椭圆转移是一种将轨道移至另一个轨道的方法。只有在最终轨道与初始轨道半长轴之比大于11.94的情况下,它才能比霍曼转移更有效。霍曼转移始终比双椭圆转移完成所需时间更短。
低推力螺旋转移用于可以使用低推力发动机(如离子推进器或太阳帆)的情况。这种推进器持续增加ΔV,并且需要比霍曼转移更多的总ΔV。
轨道平面变化是在当前和目标轨道平面之间的点处进行的,称为节点,即当前轨道与两个平面的交线(或“节点线”)相交的地方。可以进行这种操作的两个节点,可以是升交点或降交点,具体取决于从哪个方向接近它们。为了在降交点改变平面,你应该将你的航天器正确定向,使推力推动你朝向称为“轨道法线”的方向。然后,你的轨道平面将开始与目标平面对齐。为了在升交点校正平面,只需将你的航天器朝相反方向(或“轨道反法线”)定向。
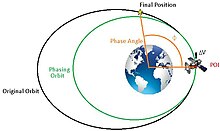
轨道定相是调整航天器轨道的真近点角,这可以通过执行两个航天器之间的交会来完成。它是通过进入一个特定的定相轨道来完成的,该轨道将使真近点角改变一个称为定相角的角度。如果航天器在同一轨道上的目标位置后面,则需要一个较小的轨道来“追赶”到该位置。如果航天器位于目标位置前面,则航天器必须进入一个更大的轨道来“减速”到该点。
为了让航天器与空间站对接,它必须首先将其轨道与空间站同步,或者换句话说,“瞄准”空间站。这是通过执行轨道定相燃烧来改变航天器的轨道周期来完成的,以便它开始“追赶”空间站。当空间站在所需的范围内时,将执行另一个燃烧,以将航天器相对于空间站的速度归零。在相对速度减少到接近零后,将进行对接操作。



