天体力学/轨道基础
轨迹方程,它给出轨道的形状,表示为
[轨迹方程]
其中B是积分常数,ν(希腊字母nu)是半长轴和位置向量r之间的角度。
让我们稍微偏离轨道的理论,并讨论圆锥曲线。人们通常熟悉圆锥曲线(圆、椭圆、抛物线、双曲线),这些曲线是从研究初等代数中得来的。但是,大多数人不熟悉圆锥曲线的形式是在标准笛卡尔坐标系中。如果我们使用极坐标系,我们可以看到所有的圆锥曲线都有类似的方程格式。我们可以概括地说,所有圆锥曲线都有以下极坐标方程
[圆锥曲线方程]
这里,r是半径,θ是角度。当θ围绕圆圈移动时,r的值会发生变化,结果产生的点会创建所需的圆锥曲线。变量p被称为参数,变量e被称为偏心率。我们将讨论这些变量,并描述它们如何与下面的轨迹方程相关。
比较轨迹方程和圆锥曲线方程,我们可以看到
变量p是圆锥曲线大小的度量。较大的p表示轨道更大。我们可以看到轨道的尺寸与卫星的角动量成正比。由于这种关系,我们可以大致了解到,卫星的速度越快,产生的轨道就越大。
e的值,即偏心率,决定了轨道将采用的形状。此表显示了e的各种值,以及由此产生的圆锥曲线的形状
| e | 形状 |
|---|---|
| 圆形 | |
| 椭圆形 | |
| 抛物线形 | |
| 双曲线形 |
查看我们的圆锥曲线方程和轨迹方程,我们可以看到
我们知道B只是一个积分常数,它不对应任何自然量。我们可以直接计算e,而无需先计算B。我们可以通过以下公式将e与卫星的能量和角动量联系起来
我们也可以使用半长轴的长度a将e和p联系起来
我们还可以定义一个偏心向量 e,表示为
[偏心向量]
该向量具有以下性质
并且 e 指向近心点(下面将介绍)。
轨道
[edit | edit source]我们可以看到,轨道方程的形式是圆锥曲线,由于这种形式,实际上可以有各种圆锥曲线形状的轨道。下面我们将讨论其中的一些。
椭圆轨道
[edit | edit source]椭圆轨道是偏心率 e < 1 的轨道。椭圆轨道是最常见的轨道之一,几乎所有绕太阳运行的天体都具有椭圆轨道。
我们从 p 的方程知道,卫星的速度会影响轨道的尺寸。我们还从 p 和 e 之间的关系方程知道,速度可以影响轨道的形状。因此,将卫星送入特定的轨道,需要赋予卫星与该轨道对应的正确速度。椭圆轨道是由低于逃逸速度的速度产生的轨道。逃逸速度,我们将在下面讨论,是指卫星摆脱主焦点的引力并形成抛物线或椭圆轨道的速度。
有一个特定的速度被称为圆周速度,在该速度下,椭圆轨道会变成完美的圆形。除圆周速度之外,所有其他速度,只要低于逃逸速度,都会产生椭圆轨道。
可以通过将适当的值代入轨道方程来创建所需的圆锥曲线,然后求解动能,来计算这些速度的值。这里将省略推导过程。
示例:地球的轨道
地球的轨道是椭圆的,尽管两个焦点距离相对较近,使得地球的轨道几乎是圆形的。因为太空是真空,没有明显的阻力或摩擦,地球的速度是恒定的,因此地球的轨道也是恒定的。从数学上来说,地球永远不会螺旋状地落入太阳。
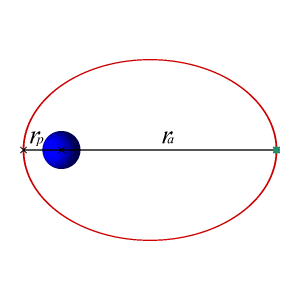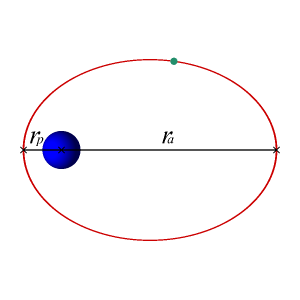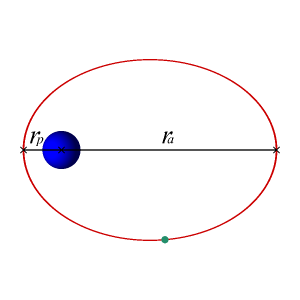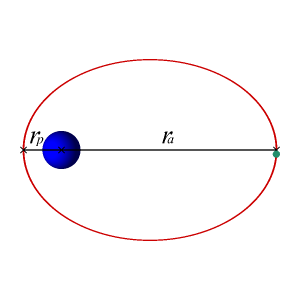
圆形轨道
[edit | edit source]圆形轨道是偏心率 e = 0 的轨道。圆形是椭圆的一种特殊情况。圆形轨道很难获得,但并非不可能。维持圆形轨道所需的速度被称为圆周速度。我们可以将圆周速度定义为
[圆周速度]
这里 r 表示圆形轨道的半径。
抛物线轨道
[edit | edit source]抛物线轨道是偏心率 e = 1 的轨道。形成抛物线轨道所需的速度被称为逃逸速度 ve。逃逸速度是摆脱主焦点的引力所需的最小速度。请注意,当我们获得这个最小逃逸速度时,我们将摆脱主焦点的引力,但我们的速度将接近零
我们可以将逃逸速度定义为
[逃逸速度]
在本例中,r 表示卫星到主焦点的距离,ver 表示从点 r 出发的逃逸速度。对于地球,该速度等于第二宇宙速度,即 11.1799 公里/秒。

双曲线轨道
[edit | edit source]双曲线轨道具有偏心率 e > 1。双曲线轨道有时也称为逃逸轨道,因为双曲线轨道允许卫星从主焦点的引力中“摆脱”,同时保持一定的速度。卫星比抛物线轨道的逃逸速度多出的速度被称为“双曲线超额速度”,vh,可以通过与发射速度(或近心点速度)vl 进行比较来找到。
与抛物线轨道相比,我们的最终速度为

退化
[edit | edit source]熟悉圆锥曲线的人可能会认识到,还有退化的圆锥曲线:点和直线。退化的圆锥曲线出现在 h = 0 的情况下,这意味着 e = 1(抛物线),但轨道将不是抛物线。
拱点
[edit | edit source]连接焦点的直线被称为长轴(在椭圆和双曲线中)。曲线与长轴交点的点被称为拱点。最靠近主焦点的点称为近心点,最靠近次焦点的点称为远心点。还有其他几个词可以互换使用
| 中心天体 | 最短距离 | 最远距离 |
|---|---|---|
| 一般 | 近心点/近心点 | 远心点/远心点 |
| 地球 | 近地点 | 远地点 |
| 太阳 | 近日点 | 远日点 |
其他太阳系天体也存在附加术语,但对于本文的目的来说,这些术语不需要。
圆形没有离中心最远或最近的点,因此近心点和远心点在圆形上是未定义的。抛物线有一个近心点,但远心点被认为在无穷远处。
从主焦点到近心点的距离可以计算为
[到近心点的距离]
从主焦点到远拱点的距离可以计算为
[远拱点距离]
注意,这些方程是通过设置 θ = 0° 或 θ = 180° 得出的,因为近拱点位于零度,远拱点位于 180 度。
活体方程
[edit | edit source]注意,在拱点处的速度必然垂直于位置向量,因此
可以推导出以下表达式
回想一下特定机械能的表达式
将 rp、vp、ra 和 va 的值代入
关于 a 求解该方程得到
[活体方程]
轨道周期
[edit | edit source]轨道的周期可以表示为
[轨道周期]
请注意,该周期仅对椭圆轨道或圆形轨道有意义,因为抛物线和双曲线永远不会完成完整的旋转。另请注意,该方程证明了开普勒第三定律。我们可以通过重新排列指数来看到这一点
现在很明显,周期的平方与长半轴的立方成正比,长半轴是到太阳的平均距离。
圆形轨道周期与椭圆轨道周期类似,但圆形的轨道半径为 *r*