生物经济学

生物经济学是关于对生物资源进行经济开发的理论，它涉及两个动态系统：种群动态和经济系统的动态。因此，生物经济学依托于两个传统的大学学科，生物学和经济学。

生产理论简要参考

生产理论是微观经济学的核心要素，简单地描述了将投入（v）转换为产出（Q）的过程

Q=Q({v_{1}},{v_{2}}....{v_{n}})\,\!

(2.1)

有多种方法可以指定此函数。一种是作为加法生产函数

Q={p_{0}}+{p_{1}}{v_{1}}+{p_{2}}{v_{2}}+...+{p_{n}}{v_{n}}\,\!

(2.2)

其中p₀、p₁、.... p_n是通过经验确定的参数。

另一种是作为科布-道格拉斯生产函数（乘法）

Q={p_{0}}\cdot {v_{1}}^{p_{1}}\cdot {v_{2}}^{p_{2}}\cdot ...\cdot {v_{n}}^{p_{n}}

(2.3)

其他形式包括恒定弹性替代生产函数（CES），这是一个更通用的公式，包括科布-道格拉斯函数，以及二次生产函数，它是加法函数的一种特定类型。要使用的最佳方程形式以及参数的值因公司而异，也因行业而异。

在短期生产函数中，至少有一个（投入）是固定的。在长期中，原则上，所有要素投入都是可变的，由管理层自行决定。

在经典理论中，生产可能涉及三种类型的投入：劳动力 (L)、资本 (K) 和自然资源 (R)。一些经典著作将后者分为两种：自然资源和能源 (E)。更常见的是，来自其他生产过程的产出被用作其他过程的投入。但原则上，应该有可能将所有投入分解为三种或四种基本类型。

短期捕捞产量

最简单的捕捞产量模型只涉及两个投入要素：一种自然资源 (x) 和一项捕捞活动（捕捞努力量，F）。

捕捞努力量的生产

让我们开始讨论一定数量的捕捞努力量的生产。此外，我们假设人力投入（可以被视为一种自然资源，但更实际的描述是劳动力）和资本（船舶、渔具等）是捕捞努力量生产中的两种基本类型投入。还假设这两种要素中的任何一种都可以被另一种要素以一定的数量完美替代。

F=F(L,K)\,\!

(3.1)

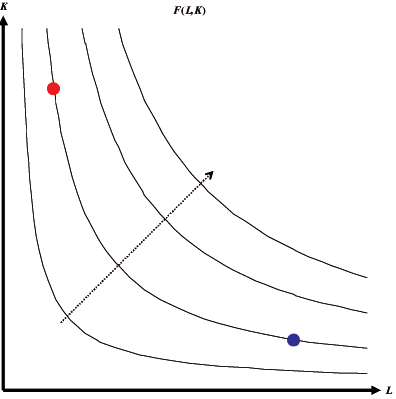
在将投入要素限制为两种的情况下，替代率可以在等产量线图中轻松查看，通常称为生产等产量线（图 3.1）。

图 3.1
捕捞努力量生产等产量线。
曲线显示L（劳动力）可以以何种速度被K（资本）替代，反之亦然，每条曲线代表F的恒定产出。蓝色点代表着一定量的捕捞努力量，其中涉及大量的劳动力投入，而红色点中大部分的劳动力被资本替代，例如小船和手线（蓝色点）与几艘拖网渔船（红色点）之间的区别。虚线箭头表示努力量生产的增加。

有效生产的概念

公式 3.1 只是对生产要素 L 和 K 如何产生 F 的技术描述，并没有给出关于哪种生产要素组合更优的建议。为了优先考虑生产特定数量 F 的不同方案，观察两种生产要素的成本会更方便。设劳动力 (L) 的单位成本为 w，资本 (K) 的单位成本为 r，则总生产成本 (C) 为：

C=wL+rK\,\!

(3.2)

可以使用拉格朗日方法在成本约束下最大化捕捞努力量的生产，这是在给定产量下最小化成本的对偶问题。拉格朗日方程为：

{\mathcal {L}}=F(L,K)-\lambda ({C_{0}}-wL-rK)

(3.3)

其中 C₀ 为给定的成本， $\lambda$ 为拉格朗日乘子。

最大化拉格朗日方程的一阶条件是方程对 L 和 K 的偏导数等于 0，由此可得：

{\frac {\frac {\partial F}{\partial L}}{\frac {\partial F}{\partial K}}}={\frac {w}{r}}

(3.4)

这个表达式被称为技术替代边际率 (MRTS)。根据公式 (3.4)，在最具成本效益的生产中，MRTS 应该等于两种生产要素的价格比率。图 3.2 展示了不同生产水平的成本效益解决方案。

图 3.2
高效生产。
粗线连接了当成本约束 C₀ 变化时，与公式 (3.4) 一致的无限多个点。

用两种生产要素生产鱼获量。

通过将捕捞努力量的生产视为一个独立的生产过程，(h，鱼获量) 的生产可以用两个生产要素 x 和 F 来表示。

h=h(x,F)\,\!

(3.5)

可以合理地假设 x 和 F 与图 3.1 中的 L 和 K 具有相同的可替代性。为了捕捞一定数量的鱼，例如 1 公斤，当种群生物量较低 (x 值较低) 时，需要投入的捕捞努力量要比种群密度较高 (x 值较高) 的情况更大。

因此，公式 (3.5) 与公式 (3.1) 属于同类，原则上我们具有与图 3.1 中所示相同的连续替代类型。

使用共同资源时的市场失灵

然而，有两个核心问题使这种生产成为一项截然不同的任务。

确定高效的生产水平需要来自完美市场的生产要素价格。在这种情况下，我们当然可以根据上面的段落计算出捕捞努力量 (F) 的完美市场价格。但另一个生产要素 x 的价格是多少？
如果该资源被视为公有财产，则价格将为零！在这种情况下，对我们想要用免费的生产要素 x 代替多少 F (F 具有正价格) 没有限制，直到该资源被完全生产并转化为鱼获量。
x 的可用性 (以及可及性) 在短期内是给定的。从长远来看，它也将是给定的，现在是过去捕捞产量的函数。换句话说，这两个生产要素相互关联！由此，生产理论中的传统方法失效。

第一个问题使我们无法继续沿用识别成本效益解决方案的常规方法。由于自然资源的稀缺性没有反映在价格中，我们缺乏关于该要素的价值信息。另一个问题也损害了我们的模型，因为它攻击了两种生产要素可用性独立性的基本假设。实际上，从长远来看，我们有：