CLEP 代数/函数

在数学中，描述某一操作中输入集如何表示该操作的输出，往往至关重要。数学为此而创造的工具叫做函数。函数的正式定义可能是一个很难完全理解的障碍，而理解它的最好方法可能是使用直观的概念进行实践（作为目标的初步步骤，即理解）。因此，我们将从本章开始，对这种“处理”过程提供一个直观的理解。

函数的直观应用和定义

您可以将函数想象成一种机器。您将原材料（作为输入）投入机器，机器将原材料转化成成品（输出）。让我们用厨师来描述一个函数。将一片生菜交给厨师，他就会将它切碎，输出就是切碎的生菜。数学中的函数有点类似。这种观点足以让我们至少了解它的实际应用。

示例 1.1(a)：日常生活中的函数 1 想象一下从桥上掉下一个球。在每时每刻，球都有一定的速度，$\mathbf {v}$。球的速度是时间的函数。这种函数被称为实值函数，因为“成品”是一个数字（更准确地说，是一个实数）。

示例 1.1(b)：日常生活中的函数 2 想象一下，一条河流的平均水温每天变化$4^{\circ }{\text{ F}}$。如果每天对河流进行水温采样，每天采样$n=30$次，所有样本的总体平均值为$\mu$，而偏差$\sigma =4^{\circ }{\text{ F}}$，那么我们可以使用以下的正态（或“高斯”）函数来反映河流水温的分布 $\varphi (x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}$ 如果相反，这条河只偏离平均水温$4^{\circ }{\text{ F}}$，那么可以用绝对值来表示 $|x-\mu |=4=T(x)$ 无论哪种方式，函数在日常生活中都有应用。

将实值函数想象成一个输入-输出机器；您将输入交给函数，它会给您一个输出，这个输出是一个数字（更准确地说，是一个实数）。例如，平方函数接受输入$4$，并给出输出值$16$。相同的平方函数接受输入$-1$，并给出输出值$1$。

人们描述函数的方式有很多种。在第一个例子中，给出了一个口头描述（球在地球上方的高度是时间的函数）。在第二个例子中，给出了某些函数的不同操作。下面将具体介绍使用操作来描述函数的方法

1. 函数被赋予一个名称（例如 $f$），同时也会给出函数的公式。例如，$f(x)=3x+2$ 描述了一个函数。我们将输入称为函数的参数（或自变量），将输出称为函数在给定参数时的值。（注意：下一节将详细介绍此记号。）
2. 函数使用方程式和两个变量来描述。一个变量用于函数的输入，另一个用于函数的输出。输入的变量称为自变量。输出的变量称为因变量。例如，$y=3x+2$ 描述了一个函数。因变量单独出现在等号的左侧。

当函数被赋予一个名称（如上面数字 1 中所示）时，函数的名称通常是字母表中的单个字母（例如 $f$ 或 $g$）。一些函数具有多个字母的名称（如正弦函数 $y=\sin(x)$。

让我们通过再次回顾第一个示例来练习使用上面描述的第二种方法分配函数。

示例 1.1(c)：球的速度作为高度的函数 想象一下，作为一名物理学家，你被要求描述速度作为高度的函数。以下是可能最适合描述的内容（使用能量方程） 在时间 $t=0$ 时，球的位置处于最大高度 $h=H>0$。 在时间 $t=T$（撞击时间）时，球处于最小高度 $h=0$（假设）。 在两者之间，球的速度正在发生变化。假设初始水平速度和垂直速度分别为 $v_{0x}=0$ 和 $v_{0y}=0$（这是因为我们丢下了球）。水平速度不会改变（假设没有空气阻力），但垂直速度会降低。因此，最终的垂直速度为 $v_{y}<0$。因此，我们只需要关注垂直速度。 以上信息使我们能够将球的速度近似为高度的函数。 $\mathbf {v} (h)=-{\sqrt {2gh}}$，其中 $g=9.81{\frac {\text{m}}{{\text{s}}^{2}}}$。

以上等式是称为复合函数的特殊类型函数的示例。此函数将在后面详细解释。现在，只需要直觉。

希望学生已经开始形成直觉。现在让我们看看如何在某些输入处评估函数。

示例 1.1(d)：给定输出的输入是什么？（第 1 部分） 如果我们写 $f(x)=3x+2$，那么我们知道 $f$ 是 $x$ 的函数。 要评估某个数字的函数，只需用该数字替换 $x$。 用右侧函数中的那个数字替换 $x$ 将会得到该特定输入的函数输出。 用英语来说，$f$ 的定义解释为“给定一个数字，$f$ 将会返回输入的三倍加二。” 基于以上要点，在某一点上评估函数的方法是 ${\begin{aligned}f(3)&=3\cdot (3)+2\\&=9+2\\&=11\end{aligned}}$ 因此，$f(3)$ 的值是 $f(3)=11$。当我们输入3 时，$f$ 在 3 处的值为 11。 请注意，$f(3)$ 表示当$x$（自变量）取值为 3 时，因变量的值。因此，我们看到，当我们输入3 时，函数的输出为11。人们经常用“3 时，$f$ 的值为 11” 或者简单地“$f$ 的 3 等于 11” 来总结以上工作。

示例 1.1(e)：给定输出的输入是什么？(第 2 部分) 让我们回到我们在示例 1.1(c) 中推导出的函数。对于函数 $\mathbf {v} (h)=-{\sqrt {2gh}}$，其中 $g=9.81{\frac {\text{m}}{{\text{s}}^{2}}}$，我们知道以下内容是正确的 速度 $\mathbf {v}$ 是高度 $h$ 的函数。 用英语来说，$\mathbf {v}$ 的定义解释为“给定地面上方的某个高度，$\mathbf {v}$ 将会根据两次重力常数与高度的乘积的平方根返回球的速度。” 在处理现实生活中应用中的函数时，重要的是要记住单位。由于使用国际单位制，重力常数 $g$ 的单位是米每二次方秒，因此高度将以米为单位。我们想要知道如果球处于桥和地面之间一半的位置，$h={\frac {H}{2}}$，速度是多少。假设 $H=9.0{\text{ m}}$。让我们开始评估函数 ${\begin{aligned}\mathbf {v} \left({\frac {9}{2}}\right)&=-{\sqrt {2g\left({\frac {9.0}{2}}\right)}}\\&=-{\sqrt {g\cdot 9.0}}\\&=-3.0{\sqrt {9.81}}\approx -9.4{\frac {\text{m}}{\text{s}}}\end{aligned}}$ 因此，$\mathbf {v} (4.5)$ 的值为 $\mathbf {v} (4.5)\approx -9.4{\frac {\text{m}}{\text{s}}}$。$\mathbf {v}$ 在 $4.5$ 处的值为 $-9.4{\frac {\text{m}}{\text{s}}}$。与 $0$ 米每秒相比，速度有了很大的提高！

关于符号的说明

函数使用非常广泛，因此有专门的符号来表示它们。这种符号有些含糊，因此熟悉它对于理解方程式或公式的意图很重要。

虽然对函数命名没有严格的规则，但使用字母 $f$，$g$ 和 $h$ 来表示函数，使用变量 $x$ 来表示自变量。 $y$ 用于表示因变量和自变量。

当讨论或使用函数 $f$ 时，重要的是不仅要了解函数本身，还要了解其自变量 $x$ 。因此，当提到函数 $f$ 时，通常不写 $f$ ，而是写 $f(x)$ 。现在，这个函数被称为“$f$ 的 $x$”。函数名与自变量（在括号内）相邻。这对于指示函数在自变量特定值时的值非常有用。例如，如果

$f(x)=7x+1$,

并且如果我们想使用 $f$ 的值，当 $x$ 等于 $2$ 时，我们将在上面定义的两边用 $2$ 代替 $x$ ，并写

$f(2)=7(2)+1=14+1=15$

这种表示法比省略自变量，只写 $f$ 更具信息量，但可能存在歧义，因为 $f$ 旁边的括号可能会被误解为乘法，$2f$ 。为了确保没有人意外地对表示法感到困惑，请遵循以下步骤

1. 通过将函数 $f$ 等于某个表达式来定义它。
2. 给出类似以下的句子：“在 $x=c$ 时，函数 $f$ 为...”。
3. 计算函数的值。

如果学生正在参加选择题考试，那么这个步骤可能会改变，因为在这种情况下，交流并不重要。

将直觉形式化

截至目前，下面的定义可能不太容易理解。请阅读定义，以便你能理解映射的概念。

函数

将一个集合（称为**定义域**，$A$）中的元素映射到另一个集合（称为值域，$B$）中的元素的映射，就是一个函数。对于从函数定义域中选择的每个值，在函数值域中都存在恰好一个相应的元素。

现在，分析一下定义。注意，值域中的元素是通过从定义域映射元素的对应关系找到的。下面给出了一个例子。

令函数 $f(x)=5x+{\frac {5x}{2}}$ 对所有 $x$ 都成立。当 $x$ 等于多少时，$f(x)=225{\frac {1}{2}}$？ 在数学中，重要的是要注意任何重复。如果某些内容似乎重复，请把它记在脑海中。 在这里，注意到 $f(x)=5x+{\frac {5x}{2}}$ 和 $f(x)=225{\frac {1}{2}}$。因为 $f(x)$ 等于两个不同的值，因此等号另一边的值必须相等。这种性质称为传递性质（永远记住实数的性质） $225{\frac {1}{2}}=5x+{\frac {5x}{2}}$ 接下来，简化——让你的生活更轻松，而不是更难。在这种情况下，由于 $5x+{\frac {5x}{2}}$ 有 $x$ 作为同类项，这两个项是加在一起的，并且是分数，所以把它放在一个共同的分母上并简化。类似地，由于 $225{\frac {1}{2}}$ 是一个带分数，所以 $225{\frac {1}{2}}=225+{\frac {1}{2}}$. $225{\frac {1}{2}}=5x+{\frac {5x}{2}}$ $\Rightarrow {\frac {225}{1}}+{\frac {1}{2}}={\frac {5x}{1}}+{\frac {5x}{2}}$ $\Rightarrow {\frac {450}{2}}+{\frac {1}{2}}={\frac {10x}{2}}+{\frac {5x}{2}}$ $\Rightarrow {\frac {451}{2}}={\frac {15x}{2}}$ 将等式两边乘以 $x$ 系数的倒数，即 ${\frac {2}{15}}$。 ${\frac {2}{15}}\cdot {\frac {451}{2}}=x$ ${\frac {451}{15}}=x$ 或 $x={\frac {451}{15}}$. 使 $f(x)=225{\frac {1}{2}}$ 的 $x$ 值为 $x={\frac {451}{15}}$.$\blacksquare$.

在传统上，从定义域中“选取”的元素被描绘成被输入函数的东西（输入），而范围中相应的元素被描绘成输出。注意这里语言的特殊性：一个输入是从定义域中选取的，这意味着定义域是所有输入的集合；一个输出是由那个特定的输入产生的，这意味着范围是所有可能的输出的集合。

由于我们“选取”定义域中与我们想要查找的范围元素相对应的元素，因此我们可以控制选择哪个元素，因此该元素也被称为“自变量”。范围中的元素不受我们控制，并由函数“映射”到。因此，该元素也被称为“因变量”，因为它取决于我们选择的自变量。由于它是一个元素，所以输入也被称为自变量。类似地，输出也被称为因变量。

函数的概念一开始更容易理解（对于大多数学生来说）。然而，函数的正式定义对于我们所知道的代数基础的重要性意味着应该高度重视函数的正式定义。然而，这并不意味着直觉是不必要的甚至有害的。相反，学生应该能够理解这两种观点，并能够将它们联系起来。因此，我们认为学生应该坚持这两种观点。

回顾一下，函数 $f$ 是将某个元素 $x\in A$（称为定义域）映射到唯一一个元素 $y\in B$（称为值域），使得 $f:A\to B$。下面的图像有助于解释函数的现代定义。

集合 $A$（定义域）将每个元素 $a$ 映射到集合 $B$ 中与其对应的元素 $b$。

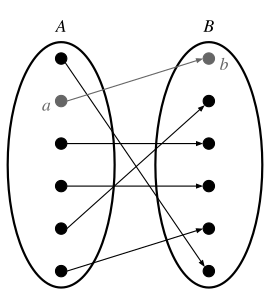
函数的基础：映射、笛卡尔积和有序对

现在我们理解了集合，我们将开始理解函数的基本属性（映射）。然而，元素是如何“映射”到另一个集合的？当组合“绑定”到另一个元素时，就会发生这种映射。在没有集合的帮助下，定义“绑定”将很困难。然而，集合很好地定义了绑定，它是通过有序对来实现的。

通过库拉托夫斯基形式化的有序对

一个有序对被定义为以 $(a,b)$ 形式书写的集合，即

$(a,b){\overset {\underset {\mathrm {def} }{}}{=}}\left\{\left\{a\right\},\,\left\{a,b\right\}\right\}$.

这里的逻辑是，包含在内的集合是一个依赖于书写对顺序的元素。因为 $\{a,b\}$ 使用了两个元素，这个集合根据书写对的顺序给出第二坐标。然而，这个定义对于 $b=a$ 不适用，因为它会得到 $(a,a)=\left\{a\right\}$，这不能准确地反映第二坐标。但是，这个定义对于本教科书的目的来说已经足够好了。此外，本文所述的知识通常不会在大学代数课程中教授。

笛卡尔积

设 $A$ 和 $B$ 是两个不同的集合。如果我们要将这两个集合合并，它将被定义为笛卡尔积 $A\times B$ （读作 $A$ 叉乘 $B$）。 $A\times B$ 是所有有序对 $(x,y)$ 的集合，其中 $x\in A$ 且 $y\in B$

$A\times B=\left\{(x,y)|x\in A\wedge y\in B\right\}$ （读作 $A$ 叉乘 $B$ 是包含有序对 $x,y$ 的集合，使得 $x$ 属于 $A$ 且 $y$ 属于 $B$。 楔形符号 $\wedge$ 是逻辑符号，表示“且”)。

笛卡尔积的本质希望不言而喻。当两个集合以这种方式合并时，就会产生有序对。这与函数的定义非常接近。毕竟，这个积的子集就是函数（在大多数情况下）。

映射

设 $A$ 和 $B$ 是两个不同的集合。一个 **从 $A$ 到 $B$ 的 **映射 $f$** 是一个关系，使得笛卡尔积 $A\times B$ 的子集 $S$ 在以下条件下导致 $f=(A,B,S)$

• 对于所有 $x\in A$ 和 对于所有 $y_{1},y_{2}\in B$,
• 有序对 $(x,y_{1})$ 和 $(x,y_{2})$ 都在子集 $S$ 中
• 暗示 $y_{1}=y_{2}$, 并且
• 对于所有 $x\in A$，存在一个 $y\in B$ 使得 $(x,y)\in S$.

符号 $f:A\to B$ 或 $A\xrightarrow {f} B$ 是对定义的简洁表示（大声读出来是 $f$ 将 $A$ 映射到 $B$）。

上述所有定义的意思是，给定称为定义域和值域的集合的笛卡尔积，存在一个有序对 $(x,y)$ 的关系，将定义域与值域联系起来。对于本书而言，首选第一个符号 ($f:A\to B$)。

使用集合查找函数的新属性

从上面的定义中，现在出现了一些新问题。以下列出三个主要问题：函数可以是（1）一对一吗？（2）多对一吗？（3）一对多吗？考虑每种情况。

1. 如果函数 $f$ 的定义域 $A$ 中的一个元素 $a\in A$ 导致值域 $B$ 中的唯一元素 $b\in B$，则该函数被认为是 **一对一** 的。根据定义，由于只有一个元素 $b$ 由函数 $f$ 从某个元素 $a$ 映射，$f:A\to B$ 意味着存在来自映射的唯一元素 $b$。因此，存在一对一函数，因为它符合函数的定义。此定义类似于 *图 1*。
2. 如果某些元素 $a_{1},a_{2},\ldots a_{n}\in A$ 来自函数 $f$ 的定义域 $A$ 映射到函数 $f$ 的值域 $B$ 中的恰好一个元素 $b\in B$，那么该函数被称为多对一函数。 由于某些元素 $\left(a_{1},a_{2},\ldots a_{n}\right)\in A$ 必须映射到恰好一个元素 $b\in B$，因此 $f:A\to B$ 必须符合函数的定义。 因此，存在多对一函数。
3. 如果函数 $f$ 的定义域 $A$ 中的恰好一个元素 $a\in A$ 映射到函数 $f$ 的值域 $B$ 中的某些元素 $\left(b_{1},b_{2},\ldots b_{n}\right)\in B$，那么该函数被称为一对多函数。 如果某个元素 $a$ 映射到多个不同的元素 $b$，那么 $f:A\to B$ 不是函数，因为存在多个不同的元素 $b$。 由于多对一不符合函数的定义，因此不存在一对多函数。

现代的函数定义足够完整，它可以帮助我们判断一种新的“函数”类型是否真的是一个函数。 现在我们已经定义了每种情况，你可以证明一个函数属于哪种函数类型。 以下是一个示例问题。

给定：$f(x)=ax+b$，其中$a$和$b$是常数，且$a\neq 0$。 证明：函数$f$是单射的。 注意函数$f$中唯一变化的元素是$x$。通过应用定义来证明函数是单射的可能是无法实现的，因为虽然定义域集合$A$中的两个随机元素可能不是一对多，但也可能存在一些元素$\left(a_{1},a_{2},\ldots a_{n}\right)\in A$使得函数成为一对多。为了解决这种可能性，我们必须证明不可能出现类似的结果。 假设存在两个不同的元素$x_{1}$和$x_{2}$，它们会导致$f\left(x_{1}\right)=f\left(x_{2}\right)$。这将使函数成为一对多。因此， $$ax_{1}+b=ax_{2}+b$$ 从等式的两边减去$b$。 $\Rightarrow ax_{1}=ax_{2}$ 从等式的两边减去$ax_{2}$。 $\Rightarrow ax_{1}-ax_{2}=0$ 从等式左边两项中提取公因子$a$。 $\Rightarrow a\left(x_{1}-x_{2}\right)=0$ 在等式的两边乘以${\frac {1}{a}}$。 $\Rightarrow \left(x_{1}-x_{2}\right)=0$ 在等式两边加上 $x_{2}$。 $\Rightarrow x_{1}=x_{2}$ 注意 $x_{1}=x_{2}$。但是，这是不可能的，因为 $x_{1}$ 和 $x_{2}$ 是不同的。因此，$f\left(x_{1}\right)\neq f\left(x_{2}\right)$。两个不同的输入不能产生相同的输出。因此，该函数必须是一一对应函数。

从函数的现代定义中可以学到一些更重要的概念，这些概念源于了解域、值域和陪域之间的区别。我们已经讨论过其中一些概念，但是了解集合的概念为以下每个概念添加了新的定义。因此，让我们根据这些新概念来讨论这些概念。下面的定义有点令人困惑。解读这些定义的最佳方法是画图。在这些定义的右侧是与其对应的图像（包括相应定义的正式定义）。

元素 $a\in A$ 是一个输入。整个集合 $A$ 是域（因为它包含所有输入）。对于任何 $r\in B$ 但 $r\notin R$ 并且 $b\in R$ 给出 $R=\{b\}$，其中 $R$ 是 $B$ 的子集，这意味着 $R$ 是值域。集合 $B=\{R,c\}$ 是陪域。

• 定义域是指一个集合 $A$，其中所有元素 $a\in A$ 都映射到至少一个唯一的 $b\in B$。
• 集合 $B=R\cup \{r\}$ 和 $R=\{b\}$ 意味着 $R$ 是函数 $f$ 在笛卡尔积中的值域，其中所有元素 $a\in A$ 都映射到至少一个唯一的元素 $b\in B$。也就是说，值域是所有被某些 $a\in A$ 映射到对应 $b\in R$ 的元素的集合。
• 陪域是指集合 $B$，不一定所有元素 $b\in B$ 都被某些 $a\in A$ 映射到。也就是说，$B$ 中所有元素的集合就是陪域。

通过使用一个能够将这些概念具体化的函数，可以使抽象概念更容易理解。假设有一个函数 $f$，其中 $x\neq 2$。令该函数为 $f(x)=2x-1$，其中 $y=f(x)$。让我们写下这个特定函数的定义域、值域和陪域。

• 域：$x\in (-\infty ,2)\cup (2,\infty )$ 或 $\left\{x|x\in \mathbb {R} \wedge x\neq 2\right\}$ 或简化为 $x\neq 2$。在这种情况下，域是集合 $A$ 中除了 $x=2$ 之外的所有元素的集合，因为这个元素不能映射到集合 $B$ 中的任何元素。
• 值域：$y\in (-\infty ,3)\cup (3,\infty )$ 或 $\left\{y|y\in \mathbb {R} \wedge y\neq f(2)\right\}$ 或简化为 $y\neq f(2)$。在这种情况下，值域是集合 $B$ 中除了 $y=f(2)$ 之外的所有元素的集合，因为这个元素不能被集合 $A$ 中的任何元素映射。
• 陪域：$y\in (-\infty ,\infty )$ 或 $\left\{y|y\in \mathbb {R} \right\}$ 或 $y\in \mathbb {R}$。这包括我们之前不允许映射的元素。

还需要定义最后一个方面。我们已经很好地了解了是什么让映射成为函数（例如，它不能是一对多）。但是，在讨论以下内容时，还需要三个你经常听到的定义：单射、满射、双射。

• 如果一个函数是一对一的，则该函数为单射。也就是说，对于 $a_{1}\in A$ 和 $a_{2}\in A$，如果 $f(a_{1})=f(a_{2})$，则 $a_{1}=a_{2}$。否则，它就不是一对一的。之前关于一对一的定义同样适用于单射（意识到单射和一对一的定义是相同的）。
• 如果一个函数是满射，它就是“到”的。也就是说，映射 $f:A\to B$ 的值域是 $B$，其中函数的陪域和值域是相同的。
• 如果一个函数既是满射又是单射，它就是双射。

以上定义经常让人感到非常困惑。为了更好地理解，在项目符号旁边提供了一张图片，并提供了一个新的例子。让我们分析函数 $g(x)=ax^{2}$。

已知：$g(x)=ax^{2}$，其中 $a$ 为常数且 $a\neq 0$。 证明：函数 $g$ 非满射且非单射。 注意，函数 $g$ 中唯一变化的元素是 $x$。让我们检查一下这个函数的条件。 它是否单射？令 $g(x)=y$，并求解 $x$。首先，用 $a$ 除。 $y=ax^{2}$ $\Rightarrow {\frac {y}{a}}=x^{2}$ 然后对 $x^{2}$ 开平方根。根据定义，${\sqrt {x^{2}}}=\left\vert x\right\vert =\pm x$，所以 $\Rightarrow {\sqrt {\frac {y}{a}}}=\pm x$ 然而，请注意我们从上述操作中得出的结论。由于求解$x$，我们发现有两个输入，$\pm x$，产生相同的输出，${\sqrt {\frac {y}{a}}}$。这意味着对于某个特定的$x$，它产生$y$，有两个不同的输入会导致相同的值。因为当$x_{1}\neq x_{2}$时，$f(x_{1})=f(x_{2})$，根据定义，它不是单射的。 它是满射的吗？ 作为对我们从输入中学到的内容的自然推论，让我们确定函数的值域。毕竟，确定某物是否为满射的唯一方法是查看值域是否适用于所有实数。确定这一点的一个好方法是找到涉及我们定义域的模式。假设我们将一个负数作为定义域的输入：$f(-x)=a(-x)^{2}=a\cdot (-x)\cdot (-x)=ax^{2}$。这个看似微不足道的练习告诉我们，负数会为我们的值域提供非负数。这是一个非常重要的信息！对于$x\in \mathbb {R}$，该函数总是产生$y>0$作为我们的值域。对于集合$B$，我们该集合中的元素没有来自集合$A$的映射。因此，$y\leq 0$是集合$B$的陪域。因此，这个函数不是满射的！

函数是数学的重要基础。这种现代解释是历史上的数学家们辛勤工作的成果。直到最近，关系的定义才由勒内·笛卡尔在《几何学》（1637 年）中引入。近一个世纪后，标准符号（$f(x)=y$）首次由莱昂哈德·欧拉在他的《无穷小分析引论》和《微积分原理》中引入。术语“函数”也是欧拉时代的一个创新，由戈特弗里德·威廉·莱布尼茨在 1673 年的一封信中引入，用来“描述与曲线点相关的量，例如坐标或曲线的斜率”。最后，函数作为集合之间关系的现代定义是由戈弗雷·哈罗德·哈代在 1908 年首次引入的，其中两个变量$x$和$y$之间存在关系，使得“无论如何，对于一些$x$的值，都会对应一些$y$的值。”对于想了解更多关于函数历史的人来说，这个页面已经为您准备好了。

函数集合定义摘要

这部分可能是最难理解的部分。本章末尾提供了总结以帮助学生进一步理解。

• 笛卡尔积是操作 $A\times B=\{(x,y)|x\in A,\,y\in B\}$，其中 $A$ 和 $B$ 是两个不同的集合。
• 映射是一种用 $f:A\to B$ 表示的关系，其中 $A$ 和 $B$ 是两个不同的集合，使得笛卡尔积 $A\times B$ 产生有序对 $(x,y)$，对于任何给定的 $x\in A$，都对应到唯一的 $y\in B$。
• 函数是指将所有输入的集合（即定义域） $A$ 映射到所有对应输出的集合（即值域） $B$ 的映射，使得对于任何 $x\in A$，笛卡尔积只对唯一的 $y\in B$ 成立。
• 元素 $a\in A$ 是一个输入。整个集合 $A$ 是定义域（因为它包含所有输入）。对于任何 $r\in B$ 但 $r\notin R$ 并且 $b\in R$ 给出 $R=\{b\}$。 $R\subseteq B$ 意味着 $R$ 是值域，如果笛卡尔积 $A\times B$ 导致 $(a,b)$。集合 $B=R\cup \{r\}$ 是陪域。
• 令 $f:A\to B$。一个函数是单射的，当对于所有 $a_{1}\in A$ 以及 $a_{2}\in A$，如果 $f(a_{1})=f(a_{2})$，那么 $a_{1}=a_{2}$。符号上，$\forall a_{1},a_{2}\in A\left(f\left(a_{1}\right)=f\left(a_{2}\right)\Rightarrow a_{1}=a_{2}\right)$。
• 如果映射$f:A\to B$ 的值域和陪域为$B$，则该函数被称为满射。换句话说，如果$f:A\to B$，则$f$ 被称为满射，如果$\forall y\in B\;\exists x\in A\left(f(x)=y\right)$.
• 如果一个函数既是单射又是满射，那么它被称为双射。

本节内容只使用专业术语。对于能够理解和翻译这些术语的学生来说，他们已经可以继续学习“检查你的理解”部分了。理解本节内容对学生来说至关重要，因为这些术语将会在后面再次出现，帮助学生更深入地理解复合函数和反函数的概念，我们将在适当的时候进行定义。此外，这些定义有时在证明中是必需的。对这些函数基本概念的良好理解将帮助学生在整个数学学习过程中受益，即使对于非数学专业的学生也是如此。

备注

以下内容是函数定义的直接结果

1. 根据定义，对于每个“输入”，一个函数只返回一个与该输入相对应的“输出”。虽然相同的输出可能对应多个输入，但一个输入不能对应多个输出。这在图形上表现为垂直线测试：一条平行于因变量轴（通常是垂直方向）的线只会与函数图交于一点。然而，一条平行于自变量轴（通常是水平方向）的线可以与函数图交于任意多个点。等效地，这在代数（或公式）解释中也是如此。我们总是可以断言，如果$a=b$ ，那么$f(a)=f(b)$ ，但如果我们只知道$f(a)=f(b)$ ，那么我们不能确定$a=b$ 。
2. 每个函数都有一组值，即函数的定义域，它可以作为输入。这组值可能是所有正实数；也可能是集合{猪肉，羊肉，牛肉}。这组值必须在函数定义中隐式或显式地定义。你不能将函数定义域之外的元素作为输入，因为函数对于该输入元素没有定义。
3. 每个函数都有一组值，即函数的值域，它可以作为输出。这组值可能是实数集。它可能是正整数集，甚至可能是集合{0,1}。这组值也必须在函数定义中隐式或显式地定义。

这是一个不满足垂直线测试的表达式示例。

垂直线测试

前文提到的垂直线测试是一种系统性的测试方法，用于判断包含$x$ 和$y$ 的方程式是否可以作为函数（其中$x$ 为自变量，$y$ 为因变量）。只需将方程式绘制成图形，并穿过$x$ 轴上每个点绘制一条垂直线。如果任何一条垂直线与图形交于一点以上，则该方程式不是函数；如果该线始终与图形交于一点或不交，则该方程式是函数。

（有很多有用的曲线，比如圆，不是函数（见图）。有些人将这些具有多个交点的图形，比如我们的圆，称为“多值函数”；他们将我们的“函数”称为“单值函数”。）