前言

这本书讲述了如何设计 CPU 及其所有组件。我的 CPU 是一款普通的冯·诺依曼机，这意味着它按顺序执行指令。我已经成功地使用 Xilinx CPLD 设计了一个 CPU，并且正在设计一个使用 Xilinx FPGA 的后续版本。之所以提到这一点，是因为我唯一能理解的编程语言是门电路 CAD，而 Xilinx 有一个很棒的程序叫做 ECS，它使这成为可能。唯一的问题是，虽然我可以编写纯门电路逻辑，但我不能编写 ROM 函数，而这些函数是指令寄存器 (IR) 所需的，指令寄存器 (IR) 包含实现所有指令的微代码。这些在 6 块 27C512 EPROM 中实现。但是，我认为可以使用 Verilog/VHDL 来实现，但我对这些语言一无所知，而且担心将 ECS 与 Verilog/VHDL 结合起来会很困难，所以我的后续计划仍然是使用外部 IR。我正在使用一种旧的架构，这意味着使用一种叫做累加器 (AC) 的东西，数据暂时存储在那里并进行操作，例如移位等。我将尝试用这本书解释你在 CPU 中需要使用的部分。

所选 CPU 架构

这里有一些模块将在后面进行详细讲解。

FA：全加器，它是所有需要进行加法操作的核心（减法通过对二进制补码进行加法来完成）

CCR：条件码寄存器，指示 FA 操作的结果，在 CCR 中设置不同的标志。

SR：移位寄存器，我使用两个 SR 来实现双向移位，我称它们为累加器 (AC)

SP：堆栈指针寄存器，该寄存器跟踪进栈/出栈操作，是暂时存储数据的另一种方法。

PC：程序计数器，它指出要使用的地址，是 CPU 的基本组成部分。

AR：地址寄存器，虽然 CPU 使用 8 位宽的数据总线，但地址总线是 16 位宽，因此需要两个字节来读取和操作地址

AND：按位 AND

OR：按位 OR

XOR：按位 XOR

IRR：指令寄存器寄存器，该寄存器从程序内存中的数据总线上读取传入的操作码，从而为指令寄存器 (IR) 设置地址，指令寄存器 (IR) 是 CPU 的真正大脑，因为它通过拉动大量的使能信号来实现每个指令/操作码，我的 IR 的数据宽度为 43 位 (IRR+BR+IRC 构成 IR 寄存器)。

BR：分支寄存器，该寄存器从 CCR 中获取 N 和 Z 标志，从而确定如何处理分支指令（以 CMP 类型的比较开头）。

IRC：指令寄存器计数器，该计数器切换实现指令所需的地址，我将其限制为 16 步。

D：内部数据总线

A：内部 ALU 总线，这条额外的总线简化了一些数据操作

OE：所有标有 OE 的方框都是三态缓冲器，在启用时将它的值放在线上，否则处于高阻抗模式。

LD：所有标有 LD 的方框都是寄存器，它们存储至少一个时钟周期 (CP) 的数据。

累加器 (AC)

此图展示了累加器的构建方式。累加器 A 和 B 只是移位寄存器，其中 A 用于将数据右移 (ROR)，B 用于将数据左移 (ROL)。不过我认为有些移位寄存器可以双向移位，但我还没有找到任何这种寄存器，因此采用了这种方法。这里我使用了三个总线 (D/A/B)，但这并不是我在 CPU 中的设计方式，目前我不太理解为什么使用三个总线。SA_A 代表移位到累加器 A 周围，这意味着移出到右边的位被放回到移位寄存器的左边。Ain_A 是要移入移位寄存器的位，LDA（加载累加器 A）是将移位寄存器从 D 总线加载数据的指令。不同的 En 代表使能，使数据能够传输到总线，禁用则给出三态输出。

移位寄存器

这个寄存器在上面被错误地命名为累加器 A/B，但它们是与我在本图中显示的类型相同的寄存器。我在 CPU 中使用这两个寄存器来实现双向移位。数据始终加载到两个移位寄存器（参见体系结构），但取决于您希望向哪个方向移位，只有那个移位寄存器用于将数据输入到内部总线。通常您无法购买 SR-触发器/触发器，而必须使用 JK-触发器/触发器，可能是因为 SR-触发器/触发器不允许输入 11 作为输入，而 JK-触发器/触发器允许（切换数据）。然而，可以使用 D-触发器/触发器来设计 SR-触发器/触发器，我认为我使用的是来自 Xilinx 库的预定义 D-触发器/触发器。实际上，我尝试使用普通 NAND 门在 ECS 中设计自己的正边沿触发的 SR-触发器/触发器，但尽管得到了 Xilinx 论坛的非常好的帮助，这仍然是不可能的。因此，我使用预定义的触发器/触发器。

Xn 是并行输入，Qn 是并行输出，LD（LDA/LDB）加载并行数据，x 是串行数据输入（Ain/Bin），当 LD 为低且 En（使能）为高时串行数据被移位，当 LD 为高且 En 为低时并行数据被加载。我将 En 称为 ROR/ROL，即右移和左移。

当进行微编码时，这工作正常，因为您只需设置您想要的信号，同时保持所有其他信号为低电平，因此如果要移位，只需将 En 设置为高电平，LD 将为低电平，如果要进行并行加载，则将 LD 设置为高电平，而 En 将为低电平。

P 和 R 代表异步预置和复位，低电平有效。

计数器

对于程序计数器 (PC)、堆栈指针 (SP) 和指令寄存器计数器 (IRC)，我们需要一个计数器。SP 也必须是向上/向下计数器，而其他两个可能只是向上计数，但为了不使用向上/向下计数器使所有计数器都复杂化，因此我使用了向上/向下计数器。

因此，PC 和 IRC 始终只向上计数，但 SP 是一个特殊的计数器，用于指向与压栈和出栈指令 (PSHA/PULA) 相关的 RAM 地址，以便能够使用所谓的堆栈来存储中间数据。您可能需要暂时存储一些数据并在以后读取，这时您会使用堆栈，而 SP 会跟踪。

通过将加载 (LD) 拉高，它能够将 Xn 数据并行加载到计数器中，输出 (Qn) 的变化将在时钟脉冲 (CP) 的正边沿出现。当加载为低电平且使能 (EN) 和向上/向下' (U/D') 为高电平时，计数器向上计数，而如果 U/D' 为低电平，则计数器向下计数。

我使用了两个时钟，分别称为 CP 和 E，其中 E 是反转的 CP，这使得可以在 CP 正边沿到来之前使用 E 设置计数器等。这在指令寄存器 (IR) 中对微指令进行编程时非常重要。

P 和 R 是异步预置和复位，低电平有效。

指令寄存器计数器 (IRC)

我将这个计数器称为指令寄存器计数器 (IRC)，这个计数器计算使用微代码实现每条指令的不同步骤。我将其限制为 16 个步骤，因此在最多 16 个时钟脉冲 (CP) 内，必须实现指令。每个步骤实际上都是一个地址，数据宽度为 41 位。

程序计数器 (PC)

这个计数器被称为程序计数器 (PC)，它是 CPU 的核心，因为它实际上是内存和输入/输出 (I/O) 的地址。它始终向上计数，因此 U/D' 为高电平。它可以使用加载 (LD) 设置一个新值/地址，如上所述。当使能 (En) 设置后，PC 随着 CP 上升而计数。

堆栈指针计数器 (SP)

这个计数器称为堆栈指针 (SP)，它指向一个小内存区域的地址，该区域使用 PSHA/PULA（将 A 压入堆栈）/从堆栈中弹出 A 指令来临时存储数据，这意味着 PSHA 将累加器 A 数据存储在 SP 指向的堆栈地址上，同时减少一个步长。如果要读取数据，请使用 PULA 指令，指针将在读取之前增加一个步长。SP 通常驻留在内存映射的底部附近，并且拥有一个相当小的内存区域，在我的情况下，它只有 256 字节大 (0000h-00FFh)。

寄存器

寄存器在 CPU 中经常使用。例如，我将指令寄存器 (IR) 的地址部分用于寄存器，我将其称为 IRR（指令寄存器寄存器），它是 IR 地址的一部分，由 IRR+BR+IRC 构成，其中 IRR 宽度为 8 位，BR（分支寄存器）宽度为 4 位，IRC（IR 计数器）宽度为 4 位。

寄存器用于临时存储数据，通常只存储一个时钟脉冲 (CP)。

当加载 (LD) 为高电平（且 CP 为高电平）时，Xn 是并行数据加载到寄存器中，然后 Xn 数据存储在寄存器（或触发器/触发器）中，并出现在输出 (Qn) 上。

P 和 R 是异步预置和复位，低电平有效。

条件代码寄存器 (CCR)

条件代码寄存器 (CCR) 读取全加器 (FA) 操作的结果。它识别操作是否为负（将 N 标志设置为 1），或者是否为零（将 Z 标志设置为 1）。它还告诉操作是否为所谓的溢出（将 V 标志设置为 1）。它甚至会嗅探传入的操作数是否为负。如果没有 CCR，分支将无法执行。

指令寄存器寄存器 (IRR)

指令寄存器寄存器（IRR）是指令寄存器（IR）的第一部分，它从程序存储器（以及数据总线）的内部 D 总线上读取传入的操作码。IRR 是 IR 的一个重要组成部分，我将其称为 IRR 只是因为缺乏想象力。

分支寄存器 (BR)

分支寄存器 (BR) 是指令寄存器 (IR) 的第二部分，它从条件码寄存器 (CCR) 中获取两个标志，分别称为 N 和 Z，其中 N 检查全加器 (FA) 操作（在比较（CMP）之前）是否变为负数或 FA 操作是否为零。这意味着如果 Z=1，则操作为零；如果 N=1，则操作变为负数。

我们可以这样写

NZ=00：操作不为负数且不为零（即为正数）

NZ=01：操作不为负数但为零（即为零）

NZ=10：操作为负数但非零（即为负数）

NZ=11：操作同时为负数和零（不可能发生）

指令寄存器 (IR)

指令寄存器 (IR) 由三个部分组成，即指令寄存器寄存器 (IRR)、分支寄存器 (BR) 和指令寄存器计数器 (IRC)，总共 16 位宽。这些模块都是寄存器，除了 IRC 是一个计数器，它们共同构成了指令寄存器 (IR) 的地址。此地址随后设置高达 41 个数据位，这些数据位随后在 CPU 内部使用，以在不同的使能信号、加载等中来实现不同的指令。所有这些数据位都非常关键，但其中两个尤其重要，它们是 Ready 和 Branch 位。Ready 信号表示指令已完成，而 Branch 信号表示有分支。当操作码为分支时，必须从条件码寄存器 (CCR) 中获取数据，以便 IR 知道该怎么做。

地址寄存器 (AR)

地址寄存器 (AR) 设置来自程序计数器 (PC) 或内部（扩展寻址模式）的地址。我为每个字节使用一个寄存器，因为数据总线 (DB) 只有 8 位宽，而地址总线 (AB) 有 16 位宽。实际上，字节是按顺序加载的，这意味着在加载完两个字节之前，地址都是无效的。在这个单个时钟脉冲 (CP) 持续时间内，AR 地址“随机”变化，但这并不重要，因为只有在完成时才会进行读或写操作。也许在 AR 之后再添加一个包含高字节 (HB) 和低字节 (LB) 的寄存器会更整洁。

数据总线 (DB)

数据总线 (DB) 是一个双向总线，实现起来有点难。我以为我已经验证了它可以在两个方向上工作，但事实并非如此。虽然我可以执行 JMP 指令，但我知道数据是从数据总线进入的，因为从程序存储器（以及 DB）中正确读取跳转地址并加载到程序计数器中，设置跳转地址。上面的架构相当准确地展示了数据总线的实现方式。它使用两个反向并联的 3 态缓冲器，高 R/W' 使能数据写入 CPU，低 R/W' 使能数据写入外部存储器或 I/O。此外，还有一个重要的特殊信号，我将其称为 D_REL，此信号以这样一种方式释放内部 D 总线，使得 D 总线可以在内部使用来循环内部数据。

全加器 (FA)

我使用的全加器 (FA) 如图所示，根据卡诺图，输出/和为

$s_{i}=c_{i}'x_{i}'y_{i}+c_{i}'x_{i}y_{i}'+c_{i}x_{i}'y_{i}'+c_{i}x_{i}y_{i}=c_{i}\oplus x_{i}\oplus y_{i}$

对于进位生成，我们有

$c_{i-1}=x_{i}y_{i}+c_{i}y_{i}+c_{i}x_{i}=x_{i}y_{i}+c_{i}(x_{i}\oplus y_{i})$

但是，此表达式是一个修复，因为如果 ci 为高，那么 xi 或 yi 为高就足够生成进位，在这种情况下，xi 和 yi 都为高并不重要。

FA 在 CPU 中一直使用，很少有指令不使用 FA。逻辑指令，如 AND/OR/XOR 以及堆栈和子程序指令以及累加器值的加载/存储（LDA/STA），是我能想到的为数不多的几种指令。大多数指令都使用 FA，例如分支、递增 (INCA)、递减 (DECA) 以及加法/减法。

然而，在 CPU 中，我们不仅要加，还要减。人们发明了一些有趣而实用的东西，那就是二进制补码。用一个数的二进制补码进行加法，实际上可以得到减法！

因此，我们不需要额外的全减器 (FS)，而是可以用一个数的二进制补码进行加法来进行减法。

分支偏移量以二进制补码形式写入，这使得程序计数器向后跳转。

一个数的二进制补码是通过对所有位进行反转并加 1 来创建的，它实际上是一个数字循环，如果我们使用 4 位的数据宽度进行简化，那么正数从 0000b 到 0111b，负数从 1000b 到 1111b，其中 1111b 等于 -1。

最高位仍然表示负数（就像使用带符号表示一样），但在这里循环中的数字方向相反，即当正数增加到 7h 并回滚到 8h 时，该数变为负数，值为 -8，而“abs”随着值达到 Fh（等于 -1）而减小。

进位生成延迟了两个 tpd（每个门的传播延迟），对于我的 8 位数据，总延迟为 16 tpd。这对于我的 CPU 的运行速度至关重要。虽然 FA 必须完成，tpd 的量级为 5ns，那么最大时钟速度（使用对称时钟，即两个“tpd”）为 6MHz，我的 CPU 无法运行得比这更快。然而，有一种称为“进位加速”的技术，但这对我来说无关紧要。

选定的指令 (CPU 汇编指令)

这张图显示了选定的指令。我决定跳过底部的两条指令，部分原因是堆栈指针 (SP) 实际上是在启动时初始化的（POR，或加电复位），并且没有必要更改它（POR 将其设置为 00FFh）。操作码是从 HCS08 中借来的，目的是不必设计自己的编译器，不过可以用纯机器代码编程，这也是我的目标。我选择的指令尽可能少，以使我的 CPU 更简单（也称为 RISC，即精简指令集计算机）。

我在 CPU 中使用的寻址模式包括立即寻址、扩展寻址和固有寻址。立即寻址意味着数据直接从外部程序存储器中读取，在图中用“dd”表示。扩展寻址意味着数据从 RAM 或 I/O 中读取，此数据类型可以称为变量，并用“hhll”表示，表示操作数是两个字节长（h 表示高字节，l 表示低字节），因为该值实际上驻留在一个 16 位地址中。固有寻址意味着我们不需要操作数，例如 INCA 仅将累加器 A 中的值加 1。

实际上，还存在另一种“寻址模式”，它有点特殊，因为只有分支指令使用它。它在图中用“rr”表示，这是一个补码形式的相对数，它在我们需要 CPU 根据条件跳转到某个地方时，设置程序计数器 (PC) 的跳转。

分支跳转

此图展示了相对分支跳转是如何完成的。例如，如果 PC 位于 28h 处，并且偏移量 (rr) 为 F8h（使用反转 + 1 我们得到 -8），那么 PC + 偏移量的补码加法结果为 20h，这意味着 PC 跳转到 20h 处。这里我们还可以看到，当第一个“字节”相加时会产生进位（因此加法必须使用 ADC，带有进位的加法）。如果 PC 位于 26h 处，并且 rr 为 +3，那么 PC 的跳转地址为 29h，但这里 V 标志被置位，在这种简化的情况下，这个溢出标志与低字节的值大于 7h 有关，在正常情况下，这意味着字节值超过 255。如果 PC 位于 26h 处，并且我们希望添加 -8，最终将到达 1E。我找不到任何问题，但已经实现了两个 EP 信号，ADD_00 和 ADD_FF，用于表示 rr 是正数还是负数。我认为我考虑得太多了，因为图中显示了使用 rr 的普通补码加法可以正常工作。

补码非常有趣。如果你想象一个圆圈，其中 0h 位于顶部，只要数字是正数，它就会顺时针 (CW) 传播，并在 7h 处停止。在 0h 的另一侧，我们有 Fh，它表示 -1，然后这个值负向增加，从圆圈的另一侧逆时针 (CCW) 移动到 8h，它表示 -8，而 Fh 表示 -1。将圆圈看作一个时钟，正数随着时间的推移而增加，负数（不带符号）随着时间的推移而减少。

CPU 定时

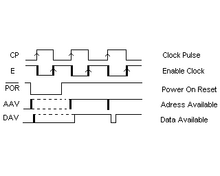
此图展示了我的 CPU 的定时。E 时钟是 CP 时钟的反相，但它被延迟了（但延迟不多，通常 <10ns，也称为 tpd，即传播延迟）。实际上，我把 E 时钟称为 EP 脉冲，因为它控制着指令寄存器 (IR) 的地址，从而在一个完整的时钟周期 (T(CP)) 内使能数据。这意味着它在一个完整的 CP 周期内使能数据。在 EP 期间，数据被使能，拉动所有数据“引脚”，但实际上在 CP 变高之前不会发生任何事情，而 CP 变化发生在 EP 的中间。因此，在 CP 来临时，EP 期间的数据是稳定的。数据可用 (DAV) 只是表明，当设置地址时，数据可用之前有一个很小的延迟 (tpd)。我通过使用 E 时钟来规避这个事实，E 时钟有一个延迟，它等于 CP 时钟周期时间的一半，产生一个 T(CP)/2 的延迟，如果 CP 频率不是太高，这足够了。

微程序控制

此图展示了微程序控制是如何完成的。指令寄存器 (IR) 中的每条指令都有 16 位的地址宽度和 43 位的数据宽度。每个数据位设置或禁用内部寄存器的不同加载 (LD) 和缓冲区的不同输出使能 (OE)，以及一些关键信号，例如堆栈指针 (SP) 是否应该递增或递减。每行由 E 时钟设置，CP 在行边界处执行，我在下面将这些信号重新命名为 EP 脉冲和 EC 时钟，它们分别代表 E 时钟脉冲 (EP) 和执行时钟 (EC)。在进行微程序控制时，这一点非常重要。

复位 (RST) 是一条仅在复位时执行的内部指令。它在 IRR 中有一个操作码 (op-code) 等于 00h，这是在 POR（即 IRR 寄存器被设置为 00h）时发生的事情，一切从那里开始。在 POR 时，PC 初始化为 FFFEh（指向起始地址的 HB 部分）。通过将 LD_AR_HB 和 LD_AR_LB 设置为高电平，这个地址在下一个 EC 时钟的上升沿被加载到 AR 中，成为一个实际地址（FFFEh 成为地址）。在下一行，R/W' 被设置为读操作，并且 LD_PC_HB 被设置为加载 FFFEh 处的跳转地址的高字节，当 EC 时钟到来时，跳转到的地址的 HB 被读取（并加载到 PC_HB 寄存器中）。同时，PC_EN 被设置为能够为下一个复位字节增加 PC（PC_LB）。当下一个 EC 时钟到来时，AR 更新为新的地址 (FFFFh)，其中包含跳转地址的 LB。在这行，我设置了 LD_PC_LB 并使能读操作。现在 PC_HB 和 PC_LB 寄存器都包含了正确的跳转地址，该地址是实际程序开始的地方。现在我们所要做的就是将跳转地址传输到地址寄存器 (AR)，我通过在最后一行将 LD_AR_HB 和 LD_AR_LB 设置为高电平来完成这一点。

在进行微程序控制时，有很多事情需要考虑，我正在考虑对 R/W' 进行反相，使其不再几乎总是为 1。这也意味着 R'/W 实际上与 OE' 相同，这就是存储器想要的，并且微程序控制被简化了（使用尽可能少的 1）。当然，CS_I/O 也必须进行修改。

下面我展示了一些非常重要的指令的微程序控制，没有这些类型的指令，CPU 就毫无意义。

LDA 微程序控制

LDA 代表 LoaD Accumulator A，这是最有趣的事情发生的地方。LDA 有两种模式，它可以在所谓立即模式（LDA#）下直接从程序存储器中读取数据，或者它可以在所谓扩展模式（LDA$）下从地址读取数据，当然微程序控制是不同的。

STA 微程序控制

STA 指令的 CPU 微程序控制

STA 代表 STore accumulator A。这条指令只能将数据存储到指定地址（即 RAM 或 I/O），这通常被称为扩展模式。

BEQ 微程序控制

BEQ 代表 Branch if EQual。这种类型的指令非常重要。如果没有分支指令，CPU 无法做太多事情，因为分支指令是让 PC 根据条件跳转到所需位置的一种方式。例如，如果你有一个条件，你想让 CPU 重复代码的一部分，你只需等待 Z 标志被置位，只要它没有被置位，指令就会重复执行（即只要操作不为零）。

这条指令不起作用，我已经尝试过了。所以不要太关注我的原理图，除了可能识别基本原理。我在下面给出了一个关于同一指令的更具教学意义的示例，我认为它可能起作用。

简化的 BEQ 微程序控制

我花了一些功夫去理解分支 BEQ 是如何实现的。我把它做得更具教学意义，虽然很多位可以同时被设置，但这样我就可以描述每个步骤。尽管如此，这个版本也是我实际可以使用的版本，因为步骤的数量正好等于 4 位 IRC（指令寄存器计数器）可以处理的步骤数量。在微程序控制方面，我决定，CP 时钟的更合适的名称实际上是 EC 时钟或执行时钟，因为我的原理图中向下每一行的边界都表示由 EC 执行，行本身使用 E 时钟，我决定将其称为 EP 脉冲，而在 IR 内部，它实际上是一个持续时间为整个 CP 周期时间的脉冲，每一行只是显示了将要发生的事情，而 EC 发生在 EP 的中间，而 E 时钟只是一个反相的 CP 时钟。换句话说，EC 在数据有效时对数据进行时钟控制，因为所有 OE/LD 等等都有一个传播延迟，必须等待它过去。

对于所有分支指令，必须在执行任何操作之前读取 NZ 标志的状态。在本例中，NZ 标志必须指示 Z=1 表示零，而所有其他组合必须被忽略。但是，所有其他组合（除了 NZ=11，这种情况不可能发生）必须被处理，并且只是增加程序计数器 (PC)，使其指向下一个操作码/指令。

我版本的 BEQ 微程序控制

这里我要对 R/W' 进行反相，使其不必总是为 1，然后我将尝试减少 IRC 步数，因为很多事情实际上可以同时启用。也许我们可以称之为“前瞻”。我不追求速度快的 CPU，我只是希望它能够工作，但如果我能减少 IRC 步数，我会很高兴。

存储器映射

这张图展示了我的内存映射，即我如何使用可用的 65kB 地址空间来分配不同的内存和 I/O。它还相当精确地展示了我如何编码不同的片选 (CS)。X-TAL (CP) 和复位已重新设计。对于 CP，我使用三个时钟，一个是使用带有开关的 SR 闩锁的“DC 时钟”，另一个时钟是使用施密特反相器产生的 1Hz 自动时钟，最后一个是我幼稚的施密特 1MHz 时钟。我只尝试过后两种时钟。

主板

为了测试 CPU，必须使用某种主板。我使用了以 nibble 为单位排列的普通 LED，高 nibble 使用红色，低 nibble 使用绿色，以便更容易读取十六进制代码。我还使用了两个外部存储器，一个是程序存储器 (ROM)，另一个是 RAM 存储器（工作存储器？），用于临时存储数据。我还使用了一个位于 16kB 地址空间内的单一地址，用于读写 I/O 数据。换句话说，我的主板/计算机不会有鼠标，而是仅与键盘和显示器交互，在原型阶段，显示器仅由两个十六进制开关组成，用于模拟键盘，以及一个原始显示器，所有数据都由我的 LED 显示。

第一块主板

这块旧主板是我第一块使用 Xilinx CPLD 的 CPU 的主板。它非常详细，因为主板是手工搭接的，没有 CAD 程序的帮助。

新主板

这块新主板是为我的 Xilinx FPGA 版本设计的。它没有那么详细，因为我计划使用 CAD 程序。可能不会使用我目前使用的 Eagle，这是因为我的免费 Eagle 版本无法处理我需要的如此大的 PCB。我计划使用 KiCAD 代替。实际上，I/O 键盘 (KB) 和显示器 (DSP) 将在位置上互换，因为如果开关最靠近你，则“手动时钟”更简单。

新版本

我决定分步进行。我将只复制第一块主板，并添加一个输出禁用 EPROM 的可能性，以便可能（观察）将 EPROM 集成到 Spartan 中。I/O 可能性将被省略，我将只专注于验证指令。如果（观察）我设法验证了所有 33 条指令，我将设计一块新的主板，以便能够构建自己的计算机。来自 5V 外部存储器（和其他）的所有信号都将串联 100 欧姆电阻连接到 Spartan（但我有点不确定这是否足够，我认为这取决于外部 IC 的电流能力）。

CPU 测试电路

这张图展示了我们 CPU 的测试电路。二进制值由两个十六进制开关设置（MSB 最上面）。在执行此操作时，该值将由最左侧的 LED 记录。当你设置了想要的值后，按下瞬时开关 SW1。然后，该值将被时钟到最左侧的下一个 LED 阵列。然后，CPU 在有空时读取该值，并通过 HC374 将该值呈现给 CPU，HC374 是一个并行可加载寄存器。如果我们将这个寄存器（一个八进制 D 型触发器）称为 IC2，那么进入 IC2 的值会在片选 (CS) 和 R/W' 为高时传播到数据总线 (DB)。如果 R/W' 为低，则写入的值会传播到较低的寄存器 (IC3)，该寄存器始终处于启用状态，它只是嗅探数据总线。正如我们在上面的内存映射中配置的那样，我们可以写入和读取到同一个地址（例如 $4000），并且在读取时获取来自十六进制开关的值，并在写入时点亮我们原始显示器的 LED。这意味着不能使用鼠标，只能使用键盘和某种显示器。

我们还添加了一些 LED 指示灯，用于指示地址总线 (AB) 和数据总线 (DB)，以及 CS 和 R/W'（指示 R/W' 的高电平和低电平）。如果你想使用这些指示灯，你必须是十六进制代码专家（所有 LED 都分成四组，使用红色表示高 nibble，绿色表示低 nibble，以简化操作）。

然而，在扩展寻址模式下，地址设置方式存在一个学术问题，因为地址是每次设置一个字节的。但是，微指令将在地址设置完成后结束，因此理论上你只会在一个时钟周期内获得一个错误的地址，该地址在那个时钟周期内是错误的。

CPU 适配器

KLD_F 是我的主板专用的 PCB 适配器。这种方法的优点是你实际上可以使用任何你想使用的 CPU（只要它是 8x16）。你只需要一个专用于你的特定 CPU 的适配器 PCB。我已经为我的 Spartan FPGA 设计了一个 PCB 适配器，其封装称为 PQ208（即它有 208 个引脚）。问题在于我的 Spartan 的可用性，很难找到。所有好东西都在不断变化，因此能够使用任何封装的概念非常棒。我实际上计划设计另外两个适配器 PCB，我将第一个称为 KLD_D，用于 DIL 型处理器（如 MC6809），另一个将称为 KLD_H，用于 PQ44（HCS08）。甚至可能有一个针对 BGA 的版本。

门电路技术

如果我们算上三态门，我们就有七种不同的逻辑门，我将在下面使用 TTL（晶体管晶体管逻辑）描述它们，而普通的 DTL（二极管晶体管逻辑）在某种程度上更有教学意义。真值表和门电路符号都已显示。所有门电路符号都采用欧洲标准。

非门（反相器）

这张图展示了一个非门。当输入为高电平时，输出为低电平，反之亦然。

与非门

这张图展示了一个与非门。当所有输入都为高电平时，它为低电平，否则为高电平。计算机中的所有东西，除了硬盘驱动器 (HD) 或一些永久性存储器，都可以用仅用与非门构建！

或门

这张图展示了一个或门。当至少一个输入为高电平时，该门为高电平，否则为低电平。符号 >1 并不完全正确，因为它应该读作 >=1，但很难放入符号中。

与门

这张图展示了一个与门。当所有输入都为高电平时，该门为高电平，否则为低电平。

或非门

这张图展示了一个或非门。当所有输入都为低电平时，该门为高电平，否则为低电平。计算机中的所有东西，除了硬盘驱动器 (HD) 或一些永久性存储器，都可以用仅用或非门构建！

异或门

这张图展示了一个异或门。当输入为高/低或低/高时，该门为高电平，否则为低电平。这意味着一个输入为高电平，另一个输入为低电平，反之亦然，都会产生高电平输出，所有其他组合都会产生低电平输出。我使用上面的符号来显示这个门。看到一个离散版本会很有趣。

三态门

此图展示了三态门。该门与非门类似，当输入为低电平时为高电平，反之亦然。但是，在这种情况下，OE（输出使能）信号必须为高电平。当 OE 为低电平时，输出为高阻抗，在此状态下，信号可以被应用于输出。这对 CPU 内部（或外部）的总线系统至关重要。

触发器技术

下面我将展示如何构建触发器及其一些关键元素。

险象生成器

此图展示了如何生成用于边沿触发触发器的险象。险象是基于门的传播延迟 (tpd) 生成的。左侧的图因此在输入信号变为高电平时会产生一个负险象，这是因为当稳定的输入为 0 时（NAND 引脚上的 01），NAND 门为高电平。但是当输入变为高电平时，反相器会在很短的时间内（tpd）保持高电平，因此 NAND 门的净输入为 11，从而产生险象。右侧的图以相同的方式工作，但会产生一个正险象。

险象的持续时间可能不足以设置例如 POR 时的计数器，但如果脉冲太小，可以将电容器安装到反相器输出端以产生更大的险象。也可以串联多个反相器以获得更大的险象。

触点抖动消除器 (SR 触发器)

此图展示了几个交叉的 NAND 门。它们实际上是一个 SR 触发器形式的存储单元（注意输入被反转）。假设 SW 处于较低位置，那么 Q' 将保证为高电平，而 Q 将为低电平，因为上 NAND 门的两个输入都为高电平。当 SW 切换位置时，Q 变为高电平，Q' 变为低电平，因为下 NAND 门的两个输入都为高电平。当 SW 处于空中时，保持前一种状态（由于 S'R'=11），并且状态切换仅进行一次。这意味着触点抖动被消除了。

如果您希望将开关连接到处理器，此设置非常有效。因此，您无需使用滤波器或特殊例程以软件方式过滤输入信号。缺点是开关需要双掷，这使得普通简单的按钮失效。

边沿触发 D 型触发器

此图展示了一个正边沿触发 D 型触发器的架构。每次 CP 的正边沿到来时（因为它根据上述内容生成一个险象），D 输入的值就会被传输到输出 (Q)。您可以移除输入反相器以获得 SR 触发器。这是数字电路中最简单的存储元素。74HC74 是一个正边沿触发 D 型触发器，可以以这种方式设计。

我尝试用 Xilinx 用于门 CAD 的优秀程序（称为 ECS）使用此方法，但不幸的是它无法实现，因此我所有的 SR 触发器都是预定义的。但是我认为我的方法是可行的。

可预置 D 型触发器

此图展示了一个正边沿触发 D 型触发器，带有异步预置和清零。因此，可以使用 R' 和 P'（低电平有效）触发触发器。这些信号在使用前必须释放到高电平，但它们是“POR”触发器状态的完美方式。POR 表示上电复位。

SR 触发器

此图展示了一个 SR 型触发器及其真值表。它是 D 型触发器的简化版本。真值表应解释为其中的值是下一个值。SR=11 不允许。

D 触发器

此图展示了一个 D 型触发器及其真值表。它在 CPU 中最常使用。

JK 触发器

此图展示了一个 JK 型触发器及其真值表。JK 触发器是 SR 触发器的扩展版本，它包含反馈。JK 触发器比 SR 触发器有优势，因为它对所有类型的输入都有定义。在 JK=11 时，它会翻转。它也可以作为封装购买，而 SR 触发器我没有找到。

T 触发器

此图展示了一个 T 触发器及其真值表。T 触发器可以在 T 为高电平时将时钟脉冲 (CP) 的频率减半。当 T 为低电平时，什么也不会发生。实际上，T 输入短接了 JK 输入，并控制输出是否应该翻转。下面我将展示一种更简单的 CP 频率划分方法。

频率划分器

此图展示了如何将时钟频率 (CP) 划分为二。它基于 D 型触发器构建。所述触发器每次 CP 变为高电平时都会改变状态。这是因为 Q' 已连接到 D 输入，因此如果 Q 为 1，则 D 会被提供 0，这会使 Q 在 CP 的下一个正边沿变为低电平。因此，一个周期需要两个边沿，这使得频率成为 CP 的一半。

RAM 内存

此图展示了如何构建 RAM 内存中的单个单元格。因此，使用一个普通的触发器（在本例中为 D 型触发器）存储了一位信息。这使得内存速度非常快。但同时，当没有电源时，它会丢失信息。它的功能是通过地址进行寻址，如果 R/W'（读写）为高电平，则读取数据，如果 R/W' 为低电平，则写入数据。由于数据输入和数据输出共享相同的总线，因此没有显示整个存储单元，因为我们还需要几个三态门。

杂项门技术

这里我将展示您如何使用不同的门配置。

单稳态多谐振荡器

此图展示了一个单稳态多谐振荡器。单词“单”表示只有一个稳定状态。该电路由触发输入 B' 上的负边沿触发，这会使输出 Q 变为高电平，持续

$T=0,72RC$

秒，这当然只对 4538 有效，但原理对所有电路都是相同的。

无稳态多谐振荡器

此图展示了一个无稳态多谐振荡器。它没有稳定状态，因此它会一直改变状态。通常，我使用一个施密特反相器（通常是 HC14）来设计我的无稳态多谐振荡器。可以证明，该电路的频率为

$f_{0}={\frac {1}{2RC\ln {3}}}$

但是对于一个单独的 4093 Schmitt NAND，我计算出

$f_{0}={\frac {1}{1,24RC}}$

当以 Vdd=5V 驱动时，其中电源 (Vdd) 对精确频率至关重要。

多路复用器

这张图展示了一个多路复用器 (MUX)。圆圈表示反相，& 表示与门，>1 表示或门。借助于控制信号 ABC，可以选择哪个输入处于活动状态并将信号传递到输出。例如，如果控制信号为二进制 110，则输入 6 处于活动状态。74HC251 是一个 8 通道多路复用器。

译码器

这张图展示了一个译码器或反多路复用器。它由多个与门和多个反相器构成。译码器实现了输入信号的所有组合。例如，如果 ABC 为 011，则与门编号 3 处于高电平。74HC138 是一个 3 到 8 线译码器。

比较器

在 CPU 中，比较两个数字的需求很常见。假设 X=<x1, x2,...,xn> 和 Y=<y1, y2,...yn>，目标是指示 X=Y 或 X>=Y、X>Y、X<=Y 中的一种情况。我们注意到 X>=Y 是 X<Y 的反相，因此我们只需要考虑两种情况（同时变量也可以互换）。

$X=Y$

和

$X<Y$

基本比较器

这张图展示了一个基本比较器，因为 xi=yi 通过一个简单的异或门和一个反相器来实现。当两个信号都为高电平或都为低电平时，输出为高电平，因此当它们相等时输出为高电平。

X=Y

这张图展示了一个用于 X=Y 的 4 位比较器。如果任何一对位不同，它们的异或门将产生一个高电平信号。当比较数字时，检查任何一个异或门是否处于高电平就足够了，因为这意味着数字不相等。如果任何一个异或门处于高电平（即表示这对位不相等），则非门处于低电平，这意味着如果非门处于高电平，则数字相等。

X<Y

这张图展示了一个用于 X<Y 的比较器。如果从最高位开始，观察到 x1'y1=1，则立即有 X<Y。如果 w2=x1'+y1=1（这意味着 x1y1=00、01 和 11，因此相等或小于）并且 x2'y2=1，则也有 X<Y。因此 Wi 表示需要检查下一位，看看 xi<yi 是否成立。

ALU 组件

ALU 代表“算术逻辑单元”，是 CPU 中执行算术计算（尤其是加法和减法）的部分。

基本加法器

这张图展示了一个基本加法器，它是一个单独的异或门。两个一位数字的加法在通过异或门后就完成了。但是缺少两件事，第一是进位产生，当两个数字都为高电平时，这是一种溢出。进位产生可以通过一个使用与门的简单加法器来实现，该与门在两个位上工作。这可以用 1+1=0 表示，进位为 1（由于与门），用于下一位。全加器 (FA) 还会处理是否从低位加法中产生了进位，并将此高电平信号（当进位时）传递到下一个单元。我认为这个事实很简单，就像如果最低位都为高电平，则按位加法为零，但有进位。现在进位被加到下一位，使进位和按位加法为二进制 10（即 2），如果还要加进位，则结果为二进制 11（即 3），因为按位加法（包括进位）现在为 1。我对这一点有点不确定，但它确实有效。也许你可以把它看成是每次加法实际上都是一个异或运算，因此如果两个位都为高电平，则异或运算产生一个低电平输出，将进位和此输出输入到一个新的异或运算，使信号变为高电平。

全加器 (FA)

我已经在上面描述过了，但为了连续性在这里显示它。虽然我已经描述过它了，但我只是提供和与进位产生的公式（这些信号来自使用卡诺图的图像）。

$s_{i}=c_{i}'x_{i}'y_{i}+c_{i}'x_{i}y_{i}'+c_{i}x_{i}'y_{i}'+c_{i}x_{i}y_{i}=c_{i}\oplus x_{i}\oplus y_{i}$

和

$c_{i-1}=x_{i}y_{i}+c_{i}y_{i}+c_{i}x_{i}=x_{i}y_{i}+c_{i}(x_{i}\oplus y_{i})$

全减器 (FS)

这张图展示了一个全减器 (FS)，它的理论和实现。假设数字是正数。如果数字是

Y=<y1, y2,...,yn>

和

X=<x1, x2,...,xn>

从 X 中减去 Y（D=X-Y）。

我不会深入研究这个问题，因为减法通常使用二进制补码加法来完成。但是，我的图中“清楚地”显示了这个原理，但我不会描述它，因为我的英语水平不是很好。但是，我将强调结果是二进制补码，并向您展示公式。

$d_{i}=x_{i}\oplus y_{i}\oplus d_{i}$

和

$b_{i-1}=x_{i}'y_{i}+b_{i}(x_{i}\oplus y_{i})'$

永久存储器 (ROM)

CPU 需要某种永久存储器（ROM，只读存储器）来获取指令。然而，这种 ROM 只能编程一次。我使用 6 个 EPROM（27C512）作为我的指令寄存器（IR）和一个作为程序存储器。由于使用的是 EPROM，如果需要，我可以重新编程它们，因为我并不擅长。

基本 ROM

这幅图展示了一个基本的永久存储器（ROM），它使用与门和或门来实现。X 表示 3 位地址总线，W 表示选择的字线，b 表示位，也就是数据总线。如果地址是 010（w2），则数据是 0110。

NAND-NAND 结构的 ROM

这幅图展示了一个 ROM，它可以称为 MROM，即机械可编程只读存储器。在这里，二极管被用于你想要设置为高的位置。因此，如果地址仍然是 010，那么 W2 将为低电平，连接到 W2 的所有二极管将向输出反相器提供低电平输出，使其输出为高电平。因此，我们与上述情况相同，但在这里我们可以使用二极管设置我们想要的数据。然而，一个 8 位数据输出（总线）最多需要 256 个二极管。所以这种 ROM 只能满足窄总线（或者如果数据大多数情况下是低电平），但它有效！

可编程逻辑阵列 (PLA)

这幅图展示了一个 PLA，它是一个可编程的永久存储器或 PROM（可编程只读存储器）。编程非常简单，因为在与部分和或部分都使用了二极管功能。对于非常小的存储器，可以使用二极管进行编程，如所示。如果我们看 w0，我们可以看到 x1'x3=1 选择它为高电平，现在 b1 和 b2 在或部分为高电平，这仅仅意味着数据输出可以使用二极管进行“或”操作。

我认为 PLA 是所有类型可编程电路（如 CPLD 和 FPGA）的更平滑的名称。

实现

一个非对称的 8x16 位架构（一个不对称的架构，意味着它在中心轴两侧没有镜像）被认为是最佳的，因为程序可以以清晰的方式编写（读取两个十六进制符号表示数据，四个表示地址），并且很容易获得外围电路，例如 EPROM 和 RAM 等。也没有什么可以阻止人们扩展到任意非对称架构模型 16x32。唯一的障碍可能是外围电路。无论如何，人们可以利用所选架构走得很远，例如，一个典型的 32kB 大程序，不仅仅是一个演示的角度来看。非对称架构的唯一问题是处理器比必要时稍微复杂一些。

高级架构

这幅图展示了我第一次尝试设计 CPU。这款 CPU 还实现了索引寄存器（X-Reg）。我个人没有看到使用索引寄存器的真正意义，所以它在下面更简单的 CPU 中被删除了。有趣的是，索引寄存器直到 1949 年之后才开始使用（根据维基百科）。然而，根据我目前的知识，累加器 A（ACC_R + ACC_L）已被准确地实现。据我所知，累加器是三件事：可并行加载的寄存器、移位寄存器和数据的中间存储器。移位寄存器功能通过使用 LSL（逻辑左移）进行乘法或使用 LSR（逻辑右移）进行除法来使用，其中只有乘以 2 的幂和除以 2 的幂是可能的（左移一次意味着乘以 2，右移一次意味着除以 2）。因此，MUL 和 DIV 在正常的 CPU 中以硬件方式实现。使用 LDA（加载累加器 A）的存储功能是最常见的，当需要将值写入 RAM 或 I/O 时，你运行 STA（存储累加器 A）。

简单架构

在这个更简单（并且使用）的架构中，我们删除了索引寄存器，删除了清除进位 (C_CL) 的可能性，并将累加器 A 简化为仅包含两个可并行加载的移位寄存器 (SR_R 和 SR_L)，也简化了堆栈指针寄存器 (SP)。删除 C_CL 的意义在于，将制作两种类型的加法指令，一种是普通的 ADD，它将两个整数相加，不考虑进位（存储在 CCR 中），另一种是 ADC（带进位相加），它将两个数字相加，考虑进位（意味着如果前一次加法产生了进位，则将考虑进位）。所以，如果你例如将 PC_LB 与一个相对的（二进制补码）分支跳转（例如 BEQ）相加并得到进位输出，那么你就可以添加 0+C+PC_HB（通过设置 ADD_00+ADC）并得到新的 PC_HB 输出。0 来自于加法必须相对于某物进行（加法器有两侧）。由于我们简化了操作，简单的指令 INCA（累加器 A 加 1）和 DECA（累加器 A 减 1）必须使用全加器 (FA) 来完成。这可以在微指令级别完成，例如，首先我们将累加器 A 加载为例如值 $FE，然后该值使用信号 ALU 放置到 ALU 总线上（并且可以在 FA 的顶部访问），然后 ADD_01（在 FA 的底部）被设置为高电平（而 ADC 被设置为低电平），这意味着 $01 被添加到 ALU 总线上的值（因此累加器 A 中的值）。在下一个时钟脉冲 (CP) 时，累加器 A 被加载为增加后的值（这里 LDA 为高电平，并且 FA 操作的结果理论上位于 D 总线上，由于 LD_FA 需要额外的 CP）。如果我们想减 1，我们可以用类似的方式完成，但使用 ADD_FF（-1）代替。这会导致 CPU 速度变慢，但目标是创建一个能工作的系统，而不是一个速度快的系统。

CPU 闲聊

下面我将讨论如何设计 CPU。即使这些图可能不相关，我将使用当前的图，一些图我确实计划更改。这些闲聊不会非常准确，只是对我的瑞典语书籍的翻译，因此可能具有一些基本的理论用途。

架构闲聊

当研究更简单的架构时，你发现 E 时钟的产生是错误的。它应该只延迟到足以使数据在内存被寻址时在数据总线（或输出）处有效（这称为访问时间）。当你看 74HC 的速度有多快时，连续四个反相器（典型的 tpd 为 80ns）不足以使用旧的内存（典型的 27C256-15 EPROM 为 150ns）。解决方案可以是：让 E 时钟成为 CP 时钟的（对称）反相，这使得所选 EPROM 的最大频率为 3MHz，或者我们可以让 E 时钟由外部产生。

这里我补充说明一下，Spartan CPU 的最大频率取决于全加器（FA）的设计方式。如果使用不带进位加速且只有 8 位数据的全加器，则 FA 的传播延迟（tpd）将为 16*tpd，而 Spartan 的 tpd 仅为 4ns。因此，如果我们使用 CP 时钟的反转技巧作为 E 时钟，则 CP 的周期时间必须是两倍，这意味着 32tpd，得出最大 CP 时钟频率为 1/(32*4ns)=8MHz。现在我看到，选择的 EPROM 会进一步限制它，降至 3MHz (1/2x150ns)。然而，这主要与外部指令寄存器（6 个 27C512）有关，该寄存器计划集成到 Spartan 中。虽然外部程序存储器的预留类型相同，但最大 CP 为 3MHz。结论是，如果我使用最快的存储器，最大频率仍然只有 8MHz（我在数据手册中看到 27C512 实际上可以制造到 100ns，但我相信还有更快的版本）。

条件码寄存器（CCR）指示算术运算的结果。它使用称为标志的信号来指示结果是否为零（Z=1）、负数（N=1）、过大（C=1）或溢出（V=1），其中 V 标志是最神秘的，它处理操作数可能都为正但结果仍然为负（由于补码）的特殊情况。例如，想象一个字节的数字范围是 -128 到 +127。如果将 30 加到 100，就会导致溢出。一开始我很难理解补码，但现在我觉得它很简单。例如，NEGA 指令将累加器中的数字取反并加 1，这给了我们补码。除了溢出之外，该数字将以正数和负数形式都正确显示。该数字的值仅取决于你如何看待它。例如，将 2 (0010) 与 C (1100) 相加，C 为 -4 或 12。结果是 E，它为 -2 或 14。

我还使用一个 H 标志，但它不是真正的半进位标志（可能被称为“半字节标志”），而是用于嗅探分支偏移的极性（它总是注入到 FA 的顶部），因此 H 是偏移的第 7 位（或 a7），它告诉我们是否应该增加（a7=0）或减少（a7=1）程序计数器（PC）的高字节。增加是通过将 PCHB 放在 FA 的顶部并添加 00h (ADD_00) 以及进位（来自之前的 LB+偏移加法）来完成的。这里 a7=0 表示正偏移。如果 a7 被置位（偏移为负），我们将 PCHB 与进位和 FFh (ADD_FF) 相加，使 PCHB 减少一步。

我不知道这是否有效，但我们可以看看几个例子（只使用 4 位）：如果偏移量为 3，输入 LB (LB') 为 6，通过简单的加法得到新的 LB 为 9（或 -7），这里 a3=0，所以这是一个正加法，新的 HB 则为 HB+C+00（其中 C 来自 LB 与偏移的加法）。如果我们有 PC'=0010 0110 (HBLB) 并且 LB' 与 3 相加，LB 就会变成 1001。这里没有进位（<15），所以 PC 应该变成 0010 1001。然后我们有 PC'=26h 和 PC=29h，因此 +3 是由于偏移！如果偏移量为 8（或 -8），LB' 为 2，LB 就会变成 10（或 -6），这里 a3=1，所以这是一个负加法，HB' 必须减少，新的 HB 为 HB+C+FF，使 HB' 减少一步（例如，从 2 减少到 1）。在我看来，当 a3 为高时，HB 总是减少一步，但是假设你有 PC'=0010 0010 (HBLB) 并且偏移量为 1000，偏移量 + LB 将为 1010 (-6)，如果我们现在减少（C=0）HB，我们最终会得到 0001，所以新的 HBLB 将变为 PC=0001 1010，而我们已经减去了 6。原始的 HBLB 为 22h (34)，新的 HBLB 为 1Ah (26)，差值 34-26 实际上是 8！然而，我对进位（C）的使用有点不确定，但如果你想添加两个数字，进位总是必须存在，例如，将 Fh 与 2h 相加将得到结果 1 + 进位，其中进位需要处理。

堆栈指针寄存器（SP）是一个可并行加载的向上/向下计数器。它在复位/上电复位时被预初始化为 00FF。在使用子程序（JSR）和堆栈操作（PSHA）时，使用它。它等待某种推送/弹出指令，例如 JSR（跳转到子程序），该指令最初将低字节（PC_LB）返回地址存储在地址 00FF 上，将 PC_HB 存储在 00FE 上。

累加器（SR_R+SR_L 或 AC）由两个可并行加载的移位寄存器组成。它被分成两部分，以便能够向右移位（除以 2 的倍数）和向左移位（乘以 2 的倍数）。真正的累加器还应该能够 INC/DEC，这表示向上/向下计数功能。然而，我们使用全加器（FA）而不是它来解决 INC/DEC。由于需要双向移位，因此在（我的世界中）累加器必须由两个独立的移位寄存器组成。它已经实现了内存功能（L/R'+LD_D）来记住使用哪个单元。可能存在可以双向移位的移位寄存器，但我还没有找到任何。最后，我认为累加器值的移位并不重要，因为“精度”很差，我只想要我 LSHR/LSHL 指令中的功能。在 STA 信号的帮助下，累加器值被放到内部数据总线（D）上，在 ALU 信号的帮助下，该值被放到 ALU 总线（A）上。因此，所有算术和逻辑（AND、OR、XOR）运算都有一个由累加器控制的专用内部总线。INV（或 NOT）逻辑函数被硬连线到全加器（FA）。

程序计数器（PC）由一个可并行加载的向上计数器组成。它专门针对新 PC 地址的 HB（高字节）和 LB（低字节）设置了两个独立的加载寄存器。它还有两个输出三态缓冲器，将选定的 PC 字节放到内部 D 总线（当 D 总线用于其他用途时，它们必须处于三态）上，该总线用于计算分支跳转，例如 BEQ。PC 之后是地址寄存器（AR），它也由两个字节组成。这些寄存器可以分别使用 HB 和 LB 加载（因为我们使用的是非对称架构）。还有一个控制信号（EXT，表示扩展），这意味着地址总线（AB）可以暂时由指令（例如 STA $AAFF，表示将累加器 A 中的值存储在 RAM（或 I/O）的该地址上）接管，并在之后将地址总线的控制权返回给 CP。

数据总线（DB）不包含寄存器。这是因为我认为不需要它，而且它甚至会破坏数据流，因为数据仍然只有在 t_acc（访问时间）之后才能使用，即在内存被寻址之后，也称为 DAV（表示数据有效）。一个寄存器将意味着需要等待另一个时钟周期。现在想象内存被寻址，并且内存地址在 CP（时钟脉冲）的正边沿被输出，同时我们有一个指令寄存器（IR）在 E 时钟（它应该是其正边沿延迟至少 t_acc 或 CP/2 的时钟，在我的情况下）下工作。在 E 时钟下，我们就可以安全地读取数据（只要 CP/2>t_acc）。例如，PC 首先被加 1，然后 AR 被加载新的地址（延迟一个时钟周期），并且内存被寻址。在这个 CP 沿上，有一个 t_acc 的延迟，然后是 DAV，但在这里，指令寄存器的 E 时钟会在 CP/2 之前等待，然后读取数据值。

指令寄存器（IR）由四部分组成。它们是两个可并行加载的寄存器（IRR+BR）、一个计数器（IRC）和一个 ROM 内存，其中选定的指令以微指令的形式实现。所有指令以操作码的形式进入指令寄存器寄存器（IRR），它始终识别这些指令。人们可能想知道为什么，但它仅仅与冯·诺依曼机的开始有关（即按顺序执行指令的机器），其中复位必须成功，并且程序存储器中的操作码必须与 IR 中的操作码列表匹配，除此之外，你必须使用正确的操作数数量来为操作码编程。我们的处理器使用三种操作数数量，分别是 0、1 和 2。操作码 + 操作数构成一条指令。然后，操作码是指令寄存器（IR）地址的一部分，在本例中是 ROM 的高字节。在分支指令（由分支作为微代码执行）时，N 和 Z 标志被加载到分支寄存器（BR）中，这成为 IR 地址的下一部分。由于我们的解决方法，这些输入在复位后将保证为零，然后在 IR 检测到分支时从 NZ 标志获取其值。在分支完成后，NZ 标志会被复位（由就绪作为微代码执行）。这样，BR 默认为 00。现在，如果有分支，NZ 的四种组合都是可能的，我们需要处理所有这些组合，除了 NZ=11 不能发生，因为一个数字不可能既为负又为零（也许这也要处理？）。指令寄存器计数器（IRC）有 16 个步骤。它通过在不同的信号（如上图中的 LDA）中抖动来依次遍历顺序微指令。所有这些都（初步）被编程到 6 个 EPROM（这里称为 ROM）中。据我所知，这些 EPROM 可以在我的 Spartan FPGA 中实现，这也是我的计划，但我会逐步进行。

微指令漫谈

这里，一直在斗争，可能离正确很远。然而，在尝试进行微程序设计时，你最突出的感受是指令深度变得很大，这意味着所有指令都需要比 HCS08 多得多的时钟周期。例如，EOR $ 需要十五个时钟周期，而 HCS08 在四个时钟周期内完成。我们在 3 个时钟周期内完成 NEGA，而 HCS08 只需要 1 个时钟周期，等等。所以，我们正在构建一个慢速处理器。但感觉它应该能够运行并完成我们想要做的事情。总的来说，作者希望我们能够在 CPLD 中编程这些微指令，这样我们就不需要外部的 41 位内存。当我们决定构建一些有用的东西时，复杂度飞速上升，真是太可怕了。

作者再次担心的是时序。我们无法充分控制取指令到达时会发生什么。就目前而言，始终运行的微指令 AR，它更新地址寄存器，应该将 PC 移动到下一条指令，同时允许读取该指令。但是时钟呢？如果 Ready 完成了指令的执行，它也可以用来加载下一条指令（因为如果我们正确地执行，当 Ready 到达时，总会有一条新的指令在等待）？我们有一个同步，其中 E 时钟在 CP 的中间变为高电平，这似乎给了我们一个很好的功能，我们可以同时做两件事，因为我们可以同时使 OE 启用并时钟输入结果，因为 OE 有时间在 CP 经过半个时钟周期后输出其信号。然而，作者对此非常不确定。

加速处理器的其中一种方法是添加一个临时寄存器，它只用于内部，并且可以在 ALU 总线和 D 总线输出数据。一个问题是，在我们获取到两个字节（例如，在 ORA $ 指令中）之前，我们不能更改地址寄存器（AR）。因此，我们必须将 HB 存储在 A 中，这导致 A 必须在存储之前被推到堆栈上，然后在我们获取到值并可以执行操作时再拉回来。使用临时寄存器，我们可以将处理器的速度至少提高 30%。另一种加速处理器的办法是，通过引入几个三态寄存器，使处理器能够到达加法器（FA）的“顶部”。始终通过 FA 也给了我们一个额外的功能，即所有数字都可以进行 CCR 检查（Z=1 表示零，等等）。

分支的实现有点特殊。当四个选定的分支操作码中的任何一个被加载到指令寄存器 (IR) 中时，标志 N 和 Z 将始终在 Branch 变为高电平的同时立即被加载。因此，我们似乎有四种不同的状态需要解码。但是，NZ=11 是无效的，因为 N 作用于 b7，而 Z 是所有位上的 NOR，所以该数字不能同时为负数和零，这就是为什么 NZ=11 被排除在外的原因。我们剩下 NZ=00、01 和 10。NZ=00 表示该数字不是负数且不为零，即 >0。NZ=01 表示该数字为零，而 NZ=10 表示该数字 <0。例如，对于 BPL，我们应该在 NZ 为 00 时执行分支，但在另外两种情况下退出并生成 Ready。但是，对于 BNE，我们必须对两种组合（00 和 10）执行分支，只在 01 时退出。

我们现在将尝试解释一些注释。AR 表示，如前所述，地址寄存器被更新（使用 LD_AR_HB 和 LD_AR_LB）。在从扩展寻址 (EXT) 或步进 PC (EN_PC) 切换时，必须始终执行此操作。我们假设操作码已正确加载，因此我们始终（除了在固有情况下）需要向前一步到第一个操作数（PC+1，AR）。我们想澄清一下，我们的程序计数器 (PC) 每次只步进一个字节，根据上面的内存配置，我们约定最高地址向下。因此，PC 始终从低地址开始，在图中向下步进（尽管我们始终向上计数）。复位后，它从第一个操作码开始，在最极端的情况下，它需要再步进两个字节才能读取所有操作数。PROM 中的存储，根据 PC 的步进方向，是操作码（1 字节）、操作数 1（1 字节）和操作数 2（1 字节），其中操作数 1 始终是高字节 (HB)，操作数 2 是低字节 (LB)。当从外部进行分配时，它用右箭头表示。内部分配，如累加器中的存储，始终用左箭头表示。数据总线上可能存在的任何东西都标记为 M（表示内存）。

乘/除杂谈

我没有在硬件上实现乘法 (MUL) 或除法 (DIV) 指令，因此我的 CPU 只能使用二进制补码进行加减运算。我选择不这样做，因为这相当复杂。真正的 CPU 确实必须实现这些指令，而我对此思考了很久。现在我认为可能可以用另一种方式来实现。

考虑一下，一个以指数形式表示的数字可以通过只加指数来进行乘法，对于除法，你只需减去指数。因此，如果这个数字可以用指数形式表示，那么 MUL/DIV 就很容易实现。

我也有这样的想法，我的 8 位只能表示大约 +/-128，但是如果字节用指数形式表示，那么可以表示像 +/-E38 这样大的数字。我的想法（不使用尾数）的问题是分辨率，因为每个相邻数字将相差 2 倍，而我的表示方式计划为

$Number=m\cdot 10^{e}=2^{bin}$

也就是说，在 CPU 中没有尾数。

如果 bin 为 128，则该数字大约为 E38，但下一个较小的数字是它的二分之一 (bin-1)。

我计算出这可能有用，因为假设你想要表示 3，最接近的 2^bin 值是 4 (bin=2) 或 2 (bin=1)，并产生以下差异

$4/3=+33\%$

或

$2/3=-33\%$

如果我们想要表示 48（介于 64 和 32 之间），最接近的 bin 值是 6 或 5，因此差异仍然是 +33%/-33% 作为最大值。

对于涉及非常大或非常小的数字的物理学来说，这非常有效。例如，我经常加减指数并将数字四舍五入到半个数量级（3.16），因此 +/-33% 接近我认为必要的精度（只要不涉及私人的经济学）。

问题是如何在将数字放入 CPU 之前对其进行转换。这必须手动完成才能获得某种精度。我的第一个公式

$Number=m\cdot 10^{e}=2^{bin}$

可以重新排列为

$binlg(2)=e+lg(m)$

或

$bin={\frac {e+lg(m)}{lg(2)}}$

这意味着要放入 CPU 的 bin 值是显示的那个，然后 MUL 通过简单的加法完成，DIV 通过简单的减法完成，这样 MUL/DIV 就不用硬件实现，至少这是我的想法。

当然，输出也必须转换，但你只需将输出从 2 提高到获得数字。

在 CPU 中使用一个普通的 8 位数字，可以通过简单的移位来进行乘法和除法。在这种情况下，8 位数字仅在 +128/-128 范围内。

左移一位表示乘以 2，右移一位表示除以 2，每次移位表示 2 的幂，因此左移两位表示乘以 4，等等。

虽然只使用 8 位的数字范围很小，但在实用性方面，这相当学术。

不过，最糟糕的情况是，假设你想要用 3 进行 MUL/DIV，而最接近的可能性是 4 或 2，那么最大差异就是 +/-33%。

我得出的结论是，我的想法根本行不通。如果我们忽略数量级的尾数，那么数字的指数将必须乘以 1/log2（3.32），而这个数字无法通过移位来实现（你只能得到 2 或 4）。使用线性表示（没有二进制尾数），你无法比 3 更接近，而当我们谈论指数时，差异太大了。

我们可以看一个例子，假设第一个数字是

$10^{11}$

而另一个数字是

$10^{15}$

我们希望将它们相乘。

用纸笔很简单，因为结果就是简单地加指数，比如

$10^{11+15}=10^{26}$

但是，如果我们希望用 CPU 将它们转换为二进制形式，CPU 必须首先将指数乘以 3.32，而这无法实现，最接近的是 4（左移两位），因此如果我们现在将 44 加上 60，我们将得到

$2^{104}$

这大约等于 E31，比它高 10000 倍（这个值也必须在输出时转换为十进制形式）。

如果我们使用我的方法，我们可以线性地设置二进制指数（但不包含小数），3,32 * 11 = 37 和 3,32 * 15 = 50，所以这个数字近似为

$2^{37+50}=1,5*10^{26}$

这个数字相当接近，但计算二进制指数意味着将十进制指数乘以 3,32，而我目前使用的 CPU 只能手动完成这个操作，3,32 只能通过移位来计算，但这显然会导致很大的偏差。

所以这种方法行不通。

另一方面，如果你看一个 8 位 CPU，如果两个操作数相等（操作是无符号的），它能处理多大数字？

256 的平方根只有 16。

因此，操作数的值（通常）必须很小，比如 16，对于 CPU 来说没什么用。

所以我得出结论，MUL/DIV 指令是没必要的。

此外，CPU 最重要的指令是 ADD/SUB，因为这些指令是 CPU 依赖的指令，比如为 PC 跳转添加分支偏移量等等。

我认为（观察到）即使没有 MUL/DIV，CPU 也能做很多事情。

我决定继续我的想法，公式在这里重复一遍

$m10^{e}=2^{bin}$

这意味着

$bin=(lg(m)+e)*3,32$

一个 MUL（微型）指令可能看起来像这样（使用两个累加器，我没有，也不会有）

1) LDA #bin_1

2) LDB #bin_2

3) ADD (B+A->A)

4) STA $[bin_1+bin_2]（存储指数和的地址）

5) LSRA #2（将 A 右移两位，从而除以 4 而不是 3,32，得到 e'）

6) STA $[e']（e' 输出，如 10^e'）

第 4 点不能完全实现，因为 bin 是线性的，没有小数，最大的偏差是

${\sqrt {2}}$

对于要相乘的每个数字，对于两个数字，偏差可能高达 2，但这是最坏的情况。偏差的计算方法是

${\frac {2^{4}}{2^{3,5}}}$

并且总是会差 2 的平方根，但这两个数字必须都离整数 1/2，才能出现这种“灾难”，你可以计算概率，因为每个数字都有三种可能的值（低、中、高），所以概率是 1/9，也就是大约 10%，但最坏情况下，两个数字相乘时的偏差是 2，所以 4 点能提供最佳容忍度（如果值是手动转换的）。

在第 5 点，我只是右移两位，除以 4（应该除以 3,32），得到 e，并将 m 设置为 1，这会导致 1,6 的额外偏差，比如

$2^{4-3,32}$

所以输出最多会偏离正确值 3,2（2 * 1,6），我用半个十年（3,16）作为计数单位，所以这不像看起来那么糟糕。

为了简单起见，我建议将 bin 值乘以 4 后放入 CPU，这样从一开始就会有额外的偏差，但使用计算器来计算要相乘的数字的步骤使得这个想法变得毫无意义，因为用纸笔更容易完成。一个完整的指数乘以 4 很容易放入 CPU。

除了第 5 点，我认为偏差会变成

$({\sqrt {2}}\cdot 2^{4-3.32})^{2}=5,1$

所以最好在将 bin 值放入 CPU 之前使用计算器，但请记住，2 是最坏的情况，如果数字更匹配，偏差只有 2,6，而且我的最大偏差只有 10% 的风险。

然而，这是在“移位生成”输出之前，如果它没有手动完成，就会产生额外的 1,6 的偏差。

我也想拥有 DIV（除法）指令，这里我需要减去指数，而我现在唯一能做到这一点的方法是使用二进制补码。这意味着 MUL 也必须使用二进制补码。我现在还不确定如何做到这一点。我在课程资料中看到浮点数实际上使用单独的符号位表示，但我的计划是使用二进制补码，具体方法我不确定。

由于我无法使用微编码来编程值，MUL 将必须是一个单独的程序。此外，如果 CPU 需要中继结果，结果必须以二进制代码形式给出。

例如，如果你想稍后添加结果，结果必须以二进制代码形式给出（在 CPU 范围内）。

所以，如果我们将 CPU 内的值定义为“CPU”，将 ADD 值定义为“bin”，同时我们想要相乘，从而添加指数，我们可以写成

$bin=2^{CPU}$

这里我们有加值（bin）的表示形式是 2^CPU，这意味着 CPU 存储着指数版本，而我使用 8 位，CPU 值最多可以是 8（n）。

现在，如果我们通过添加两个 CPU 指数来相乘两个数字，我们可以说这个新数字是 CPU'，所以现在 bin' = 2^CPU'

这里我们需要创建一个表，CPU' 不能大于 8，我们只能表示线性 n，所以我们需要将中间值设置为没有小数的 n，比如 [0;1] = 0，[>1;2] = 1 等等，这种情况下最大的偏差是 2。

输入时也会发生同样的情况，CPU 只能有整数值。在输入时，CPU 可以定义为

$lg(bin)=CPUlg(2)$

或

$CPU={\frac {lg(bin)}{lg(2)}}$

我们需要一个lg(bin)的表格，但是我的CPU无法进行计算。

所以我们需要两个表格，例如：

$2^{CPU}$

和预备的：

$lg(bin)$

实际上，如果你使用：

$lg_{2}=3,32lg_{10}$

就可以消除lg2，从而可以写成：

$CPU=lg_{2}(bin)$

所以我们需要一个lg_2(bin)的表格，其中bin小于255。

一个这样的程序看起来像是：

MUL(bin_1, bin_2)

CPU=lg2(bin) [需要表格]

ADD CPU(bin_1, bin_2)

Bin=2^CPU [需要表格]

这可以在CPU中进一步传递，因为它是纯HEX代码，这意味着结果可以稍后使用。

然而，我的最初想法是将一个10进制指数数字替换为一个2进制指数数字（其中2进制数字缺少尾数）。在这里，我们可以通过简单地将指数相加来将两个2进制数字相乘。此外，可以表示相当大的数字（~E38）。对于加法，我们只需使用具有最大指数的数字（并跳过另一个）。

为了能够在CPU内部传递一个数字，它必须是纯8位HEX类型，而且不可能用二进制代码写出E38，所以这个值无法在CPU外部显示。

如果我们坚持使用“128”，我们就可以操作它并将其呈现给外部世界，唯一的问题是这个数字不能大于128。

虽然我们可以在CPU内部正式表示E38，但我们不能在CPU外部使用它，但只要我们将其保持在CPU内部，它就可以工作，但在外部它只能表示为指数。

我得出的结论是，DIV不能用我的想法实现。原因是我只能使用二进制补码进行减法，而这根本行不通。我正在考虑浮点数的结构，它似乎有一个符号位，而其余部分始终是一个正数。这对于MUL来说很好，因为指数只需要相加，但是对于DIV来说，指数需要相减，而我无法对不是二进制补码的数字进行减法。

可能存在一种解决方法，可以将无符号数字转换为二进制补码，但是当使用8位和7位时，它们是正数（使用浮点数），而二进制补码的数字表示范围仅在+/-64左右。

这是因为我们有一个符号位（b7），它给出其余部分的二进制补码为+/-64。

我不知道如何或是否可以将正数转换为二进制补码，除了如果b6=1，则该数字为负数，所以要使用的数字是该数字的反转+1吗？

此外，对于MUL和DIV，我都需要使用表格来转换

$bin=2^{CPU}$

和

$CPU=lg_{2}(bin)$

而且这些表格远非精确的。

虽然我已经得出的结论是DIV不能使用二进制补码，但我决定使用相同的数字表示方法来进行MUL/DIV，即最初使用二进制补码，计算过程中使用符号大小，最后使用二进制补码作为输出。

使用二进制补码表示“bin”的原因是我的CPU在内部使用它，因此生成的数字可以在CPU内部稍后使用，另一个原因是我喜欢正数和负数。实际上，摩托罗拉似乎在其超级MC6809中使用硬件实现的MUL/DIV，仅使用无符号数字，所以在这个方面（仅限于此）我的版本更好。

以下是我的MUL（8位）算法：

MUL(bin1, bin2)

b7=1=>NEG(bin)+1=abs, s=1 [8位]

b7=0=>bin=abs, s=0

s1 XOR s2=s [存储]

s.abs=Number [符号大小，8位]

Number'=Number AND 7Fh [7位，<64]

CPU=lg2 Number' [表格，我们的指数]

ADD CPU(Number1', Number2') [指数相加]

abs=2^{ADD} [表格，我们的量级]

s=0=>out=abs [来自上面存储的s]

s=1=>out=NEG(abs)+1

out=7位二进制补码

这种解决方案的缺点在于，它仅涵盖+/-64的数字范围（但我认为可以通过乘数来增加，但数字之间的步长将是乘数），部分原因是，虽然我的CPU无法正确计数，我必须使用表格，但精度很差。但是，我已经计算出最大误差为2.8，这低于我在进行物理计算时允许的半个十年的3.16。

以下是我的DIV算法：

DIV(bin1, bin2)

b7=1=>NEG(bin)+1=abs, s=1 [8位]

b7=0=>bin=abs, s=0

s1 XOR s2=s [存储]

s.abs=Number [符号大小，8位]

Number'=Number AND 7Fh [7位，<64]

CPU=lg2 Number' [表格，我们的指数]

SUB CPU(Number1', Number2') [指数相减]

abs=2^{SUB} [表格，我们的量级]

s=0=>out=abs [来自上面存储的s]

s=1=>out=NEG(abs)+1

out=7位二进制补码

以下是我的第一个表格（二进制数字的2的对数）：

CPU=lg2 bin Table [7位]

bin=[(>0);1]->CPU=0

bin=[>1;2]->CPU=1

bin=[>2;4]->CPU=2

bin=[>4;8]->CPU=3

bin=[>8;16]->CPU=4

bin=[>16;32]->CPU=5

bin=[>32;64]->CPU=6 [2^6=64]

这里的误差为2，而CPU是指数，2^1=2，但这是一个最坏情况。

以下是我的第二个表格（CPU从2开始的bin）：

bin=2^{CPU} Table [7位]

CPU=0->bin=1

CPU=[>0;1]->bin=2

CPU=[>1;2]->bin=4

CPU=[>2;3]->bin=8

CPU=[>3;4]->bin=16

CPU=[>4;5]->bin=32

CPU=[>5;6]->bin=64

这里的误差显然是2，当然这是最坏的情况。

因此，总最大误差为4（而不是我之前计算的2.8）。但是，4并没有比我允许的3.16大很多，所以我的想法仍然可以使用。

新想法

我认为我现在有了另一个更简单的解决方案，关键是创建一个3.32(1/lg2)的因子，用于乘法和除法。二进制指数必须除以3.32才能得到十进制指数，十进制指数必须乘以3.32才能得到二进制指数。虽然这些是指数，但如果我们例如将数字左移两次来进行四倍的乘法，那么误差会变得相当大。

那该怎么办呢？我们需要用大约3.32进行乘法和除法。我的朋友们，解决方案可能在于两个外部模拟乘法器/除法器，这样我们就不需要单独的数字乘法器或除法器了！

我的I/O内存映射为16kB，我的计划是仅使用此区域内的1个I/O地址，以便能够输入（键盘）和显示（显示）值，在同一个地址进行读写。

但是，如果我想实现这个新想法，我需要使用两个额外的I/O地址（一个用于模拟乘法器，另一个用于模拟除法器），并且需要重新配置I/O芯片使能。如果你问我，这是一个相当不错的想法，这里有一个例子

$10^{x}=2^{e}$

这意味着

$x=e\cdot lg2$

其中

${\frac {1}{lg2}}=3,32$

唯一的问题是x将变成一个分数值（即不是整数），因此输出x不是整数，而我们习惯读取尾数乘以整数指数。但是x可以转换为整数并得到一个尾数，但这意味着使用计算器。另一方面，保留在CPU内部的值可以传递给其他指令。我不知道我是否正确，我只是写下了我的新想法。

另一个让我印象深刻的是，例如，如果你将两个无符号的半字节数相乘，不同的数字必须在 16 的范围内才能不溢出 256。但我可能在这里理解错误了，实际上这些相当小的数字是一种分辨率，比如 1/16-16/16，就像尾数在 0-1 的范围内一样，这种分辨率是 6.25%，实际上并不算太糟糕，因为假设我们使用 5V ADC，6.25% 意味着 LSB 为 0.3V。我不知道我们是否可以这样计算，但我认为在实际情况下，这种较差的分辨率并不算太糟糕，并且系统将适应更大的值，即使存在更大的绝对误差。

今天我突然想到了一件微不足道的事情，CPU 外部的值是十六进制 (Hex)，对于正常使用来说，这与 CPU 内部 (CPU) 的值相同！我最终理解这一点的方式是，对程序存储器进行编程意味着纯粹的十六进制代码，我们必须将十进制数字转换为二进制代码。因此，我们在这里不使用十进制数字，来自键盘的外部数字 (观察) 虽然是十进制的，但我们在 CPU 工作时会将它们转换。现在我的计划是通过加减指数来实现乘除，所以我必须将上面的公式改为

$Hex=2^{CPU}$

虽然 Hex 只有 8 位，因此最大值为 256，但 CPU 必须具有最大值为 8 的值，这意味着 3 位，而 CPU 是线性二进制代码。对于相同的二进制“宽度”，Hex 使用所有 8 位，而 CPU 仅使用 8 位中的 3 位。虽然 CPU 是线性二进制代码，每一步都是一个整数，但中间的值将不得不被四舍五入，但两个值都可能在整数之间，无论如何，误差不能超过

${\frac {2^{2}}{2^{1}}}$

也就是 2。我计划使用外部模拟 2.32 乘除和对数/指数实现，这些实现将非常精确，因此这里没有额外的误差。同时，这个误差也是最坏的情况，因为看一个实际情况，比如 CPU 值在 1 和 2 之间，这个实际的最坏情况意味着这个值应该是 1.5，但碰巧是 1 或 2，现在这个实际的差异小于 sqrt(2)，但最好不要期望超过这个值。

我已经找到了一种方法可以进一步减小这个误差（我得到了 4%），方法是在指数中注入尾数，比如

$Hex=2^{m/n+CPU}$

其中 m 是尾数，n 是尾数的二进制宽度，产生 m/n 在 [0;1] 的范围内。我最近发现，用数字的宽度相除实际上意味着将 m 右移 n 次。这里我们只需要处理移位出去的位。让我觉得有趣的一件事是，我们如何知道移位实际上给出了一个分数？但我认为我已经得出了结论，我们不知道，就像 LSB 不需要是权重 2^0 一样，而这只是我们对数字的简化视图，2^0 可以很容易地是 2^10，但相对来说，它仍然是正确的，因为位不知道它们的值！

但是，我不会关心 sqrt(2) 的最大差异，因为这样一切都变得更简单。我坚持使用纯指数形式，而我的计划是将指数相加以进行乘法。在这里，我想出了一个类似于

$CPU=3,32lgHex$

所以我的步骤是
Hex->D/A->模拟对数=>3.32lgHex->A/D->CPU
CPU/3.32->D/A->模拟指数=>10^(CPU/3.32)->A/D->Hex

在这里，我必须将 CPU 的 A/D 限制为仅 3 位/8h，但 Hex 输出的 A/D 可以具有完整的 8 位分辨率。现在我可以使用仅指数（CPU）来乘除数字。然而，一切都从我的第一个假设改变了，现在我需要两个模拟设备来实现

$3,32lg(x)$

和

$10^{(y/3,32)}$

我非常确定增益部分可以用相同的模块实现。我计划使用 LM13700，我手头有一些，但我并没有完全理解这个神奇的 OTA（输出跨导放大器），但我已经用它设计了一个 RMS 电压计。需要注意的是，对数和指数函数也可以用一个简单的二极管来模拟。

最后，我当然可以在数字上实现 MUL/DIV，但经过认真研究，我并没有完全理解它们，我遵循的原则是我不使用我不理解的小工具（因为调整将是无望的）。正如我所说，我也不理解 OTA，但我对模拟设备更熟悉。

今天我醒悟了，虽然上面在理论上是可行的，但我认为在实践中它行不通，因为存在几个问题，如果我从 CPU 可以根据上面的方法从 Hex 中获得一个正确的值（带有容差）这一事实开始。因此，我们在这里被一个值困住了，而 CPU 的表示是按位进行的，所以如何将一个数字转换为位流？用纸笔很简单，但自动呢？例如，看最高位，这个位被计算为尽可能精确地表示这个数字。在我的世界里，你会从原始值中减去这个新的值，并逐位继续这个过程。但最初的测试怎么办？这个测试不是数字的，而仅仅是原始值的截断，同时估计 n_max。虽然我的原始 CPU 只能加减，但这听起来相当不可能。另一个问题是，我真正想要的是二进制补码形式的数字，那么真的存在能够处理这种情况的 ADC 和 DAC 吗？我知道我最喜欢的 ADC（TDA8703）可以，但偏置怎么办？我认为连接用于二进制补码的 ADC 必须具有等于转换范围一半的直流输入偏置。对于 DAC，如果存在二进制补码 DAC，则模拟输出值也必须等于转换范围的一半，这意味着输出总是直流的。

专业 MUL/DIV 算法

在这里，我将尝试解释两种分别用于 MUL 和 DIV 的算法。这些算法可以用于在 CPU 内部实现硬件 MUL/DIV，但我将尝试创建一个“软件”版本。这当然会使我们的 CPU MUL 和 DIV 比必要的速度慢，但它可能是实现它们的一种更具教育意义且更简单的方法。

MUL（罗伯逊算法）

我将用一个图片示例来展示这一点，但这里我只是随意谈谈。

如果我们将一个数字称为被乘数 (y)，另一个数字称为乘数 (x)，那么我们有

y=被乘数 <y0, y1, y2...yn>
x=乘数 <x0, x1, x2,...xn>

这里 x 乘以 y，所以如果 x 为 0，则不添加任何内容，但如果 x 为 1，则添加整个被乘数。

我在我的《数字技术》书中发现了一种名为 Robertson 算法的算法，该算法阐述了

$p^{0}=0$
$p^{i+1}=(p^{i}+y\cdot x_{n-i})2^{-1}$
$i=0,1,2...n-1$
$p=p^{n}-y\cdot x0$

其中 p 是部分积，最后一个是积。该算法实际上使用二进制补码中的数字，n 然而不包括“符号位”，因此如果一个数字是 8 位二进制补码，n 是 7。

使用我书中的示例，我得到了一个解释，如下所示（小数点左侧表示符号）

1) p^0=0.0 (sign.2n)
2) 与 x(n)*y 相加（y 向左移位 n 次）
3) 取和
4) 向右移位一步，得到 p^1
5) 与 x(n-1)*y 相加
6) 取和
7) 向右移位一步，得到 p^2
8) 重复此操作直到最后一位 (p^n)，然后减去 y*x(0)

如果 n 为 4（两个 4 位数据，不包括符号位），2n 将为 8 位，因此 p(0) 为 8 位长，我们需要将被乘数左移 4 位，并创建一个由乘数决定的值（乘以被乘数），即，如果乘数中的乘位为 0，则添加 0，但如果乘位为 1，则添加整个被乘数 (y)。然后位置 8 就很有意思了，因为如果乘数的符号位 (x(0)) 为 0，则该数字为正，我们只需将 0 添加到 p^4，但如果符号位为 1，则 y 在添加之前取反，从而产生二进制补码乘法。

在进一步研究 Robertson 算法的过程中，我首先得出结论，负值并不必要，因为您可以自己识别它们，其次，如果我的数据总线是 8 位（并且我们使用无符号数），则结果将为 16 位类型。因此，虽然我只能处理 8 位，但被乘数和乘数必须分别最多为 4 位。现在，16 的值并不大，但通常情况下，通过使用尾数+指数，我们只需要将尾数相乘，而在实践中，尾数是一个不超过 1 的小数，而 1/16 (0,063) 是一个相当好的步长近似值。虽然我的数字只是整数，但这种情况在我的情况下却无法使用。

另一方面，我认为我在这里错了，虽然我们可以识别数字是负数还是正数（并进行转换），但 CPU 本身却无法识别，因此，如果 CPU 给出一个负值，并且该值随后用于乘法，则 CPU 必须能够处理负数。然而，摩托罗拉公司在其出色的 MC6809 中，仅为无符号数硬件实现了 MUL/DIV。因此，似乎仅使用无符号数是有道理的。二进制补码也存在一个问题，因为“数字”此时仅由 7 位表示，这使得两个操作数都需要为 3.5 位。

我还得出结论，我无法用我当前的 CPU 实现 Roberson，因为我无法使用进位右移（或 1），只能移入 0。但是，我有一个松散的计划来实现一些新的指令，我称之为 CSRA（进位右移累加器 A），但我确实不想重新编译我的 Spartan。虽然我不使用尾数，但这有点没有意义，还是我错了？

如果被乘数和乘数在理论上分别为 16（4 位），则积将为 256（8 位），那么我们有一个最大为 256 的积。现在，我们想要达到的值大约为 1/h~E34，对于 E34，我们需要 113 位。因此，使用 4+4 位来达到 E34 是没有意义的，唯一的方法是改为只将尾数相乘，然后将指数相加。这被称为使用浮点数，但我不想实现它。

如果我不实现浮点数（或尾数+指数），那么 MUL 对我来说就没有什么实际用途，DIV 可能也没有，因为会有余数需要处理，我想。然而，Robertson 算法很有趣，我会尽力解释它，并想出一种汇编程序（可能使用我没有的指令）。

看看我的图片，我们可以发现如何进行乘法，我也列出了我的方法。Robertson 算法实际上也适用于二进制补码，但展示它需要做太多工作，所以我只展示了正数的 Roberson。正如我们在这里已经看到的，存在一个“问题”，因为进位必须得到处理（而我只能移入 0）。然而，最左侧的基本算法非常有趣。唯一的问题是要添加四个（左移的）数字，但我不知道这有什么大不了的。下面是一个伪汇编程序尝试：我在这里放弃了，因为我实际上需要将乘数的有效位与被乘数相乘，而我没有实现 MUL。然而，移位部分不是问题，因为我可以移入 0（LSLA/LSRA）。

但也许
LDA $y [四位，从 I/O 加载]
STA $y_value [存储 y 以供日后使用]
LDA $x [四位，从 I/O 加载]
AND #$01 [A<-A AND M]
STA $bit4，即 bit4 的地址
LDA $x
AND #$02
STA $bit3
LDA $x
AND #$04
STA $bit2
LDA $x
AND #$08
STA $bit1
LDA $bit4
CMP #$01
BEQ $04 (JMP 地址为两个字节)
JMP Next1 (在 BNE 处完成)
JSR $Add_x_with_y，A<-x+y，将和存储在 $sum4 中
JMP Next2
Next1:JSR $Add_0_with_y，A<-0+y，将和存储在 $sum4 中
Next2:LDA $bit3
CMP #$02
BEQ $04
JMP Next3
JSR $LSLA_y_and_add_with_$sum4，将和存储在 $sum3 中
JMP Next4
Next3:JSR $LSLA_y_and_add_with_0，将和存储在 $sum3 中（这里对 y 进行了正式移位）
Next4:LDA $bit2

等等

这不是一个快速的“算法”，但我可能会完成它。摩托罗拉在其 MC6809 的数据手册中没有说明需要多少个时钟周期，但它一定超过了 8 个。我使用了 26(+12) 个指令，其中最快的约为 5 个时钟周期。假设 32 个指令用于两个无符号四位数，如果我们使用 1MHz，那么大约需要 32*5*1us=160us。然而，不需要等待，就像 FA 操作一样，因此只需要 160us，这并不算太糟糕。但是，我还没有计算出不同子例程的速度，因此 160us 是低估了。

我现在发现，HCS08(MUL) 对于两个 8 位数只需要 5 个时钟周期。令人惊讶的是，MUL 是硬件实现的。

我做了一些更改，因为子例程中的 RTS 会使程序返回并执行下一个地址。因此，如果下一个地址意味着另一个条件，那么也会执行该条件。换句话说，我们不能同时执行 y+x 和 y+0 的加法。

MUL（Booth 算法）

Booth 算法在硬件实现方面更流畅，因此我也研究了该算法。我得出结论，我需要进行乘法和除法。虽然我只使用了一些 4 位分辨率的整数，但我认为与不超过 16（无符号）的数字相乘似乎毫无意义，但请看您是如何例如绘制一个函数来了解它的形状。我认为您很少用超过十的“x”来绘制，例如，如果您想绘制一个二极管函数到 200mA，除非我进行缩放，否则我无法处理它，但我也可以绘制到 2 或“16”。您只需进行缩放！因此，重点更多在于分辨率，例如您需要多少个步长？16 个步长是一个相当好的近似值。我现在想在硬件中实现 Booth，也许还会创建一个新的 Mathlab :-D

另一个要创建的是函数的泰勒展开式，考虑到二阶，您需要进行乘法和除法（用 2!），并且您通常在接近于零的某个点评估泰勒展开式。因此，这些数字并不大。

我将继续我的 CPU 任务，主要测试我当前的指令，只有当我能够使所有 33 个指令都能正常工作时，我才会在硬件中实现 MUL/DIV，而我之前用软件实现它们的方法似乎不起作用（而且速度会很慢）。原因是我大约 10 年前编译了我的 Spartan，除非遇到任何指令的故障，否则我不想重新编译。

算法是这样的

$x_{5}=0$
$p^{(0)}=0$
$p^{(i+1)}=(p^{(i)}+y\cdot (x_{5-1}-x_{4-1}))2^{-1}$
$i=0,1,2,3$
$p=p^{(}4)+y\cdot (x1-x0)$

这两个二进制补码数字都是 5 位。

加法器中的不同单元有五个信号：进位输入、进位输出、x 输入、y 输入和和输出。进位是一个链，贯穿每个单元，但 x、y 和和始终可以在本地访问。我已经在上面的书中写过全加器 (FA) 的工作原理。

DIV（Burk 算法）

除法可以使用 Burk 算法进行，其过程如下

$r^{(0)}=x$
$z_{i-1}=(r_{0}^{(i-1)}\oplus y_{0})'$
$r^{(i)}=2r^{(i-1)}+(1-2z_{i-1})y$
$i=1,2,3,4$
$q=z+2^{-4}-1=z+1/16-1$
$r=r^{(4)}\cdot 2^{-4}$

其中一个数字/被除数 (x) 可以定义为

x=qy+r

其中 y 是除数，q 是商，r 是余数。

第一个余数 r(0) 当然是完整的被除数 (x)，r_0 是余数的符号位，z 有点特别，但它处理了这样一个事实：如果前一个余数为负，则余数的后续近似值会使新的余数变小（因为它减去了）。只要除数和余数为正，z 就为低。z 的权重为 2^(-n)，因此对于 z0，权重为 1；对于 z1，权重为 2^(-1)，依此类推。别问我关于这个 : :)

我一直很难理解这一点，我现在仍然不明白。但我已经看到它有效。关键是要理解 r_0 是前一个余数的符号。

在图片底部，我展示了一种用顺序硬件实现除法的方案（我从我的 Danielsson 数字技术书籍中复制了它，但我很难理解。然而，他似乎知道自己在做什么，所以我认为这是解决除法问题的正确方案）。但我确实认为顺序方案可能紧凑而简洁，但会依赖于 CPU 时钟。在我的例子中，我并没有为高速 CPU 设计，我只想让它工作，但我认为组合方案更好，因为这里 CPU 时钟不会限制速度，而是门的传播延迟会限制速度。然而，这里的问题是门的数量会增加。

MUL/DIV 实现

我的计划是只使用字节（虽然我没有 16 位索引寄存器）。这意味着两个二进制补码数字的乘积必须小于 8 位作为结果。然后每个数字都是 4 位，而值部分可以说只有 +/-7，因为只有 3 位。然后将这些数字合并成一个 8 位数字，以便低半字节表示例如被乘数的二进制补码，另一个半字节则表示乘数。然后二进制补码积是 7 位宽。对于除法，我将使用相同的方法，使用一个半字节显示二进制补码余数，使用另一个半字节显示二进制补码商。

我认为，+/-8 左右的值范围并不像听起来那么糟糕，因为它意味着 1/8 的分辨率，即 0.125，因此如果你想表示圆周率，例如，你可以设置为 3+1/8，这相当接近；如果你想表示 4,9，你可以设置为 4+7/8，这也相当接近。

我认为乘法的用途是利用直线的方程式来击中“斜率”点。斜率来自导数，你需要用类似于

$y=y_{0}+k(x-x_{0})$

的导数来击中该点，其中 k 是导数，这里很明显，如果你想击中该点，你需要进行乘法运算。但我认为这可以进行缩放，这样你就不需要任何大的（或小的）数字，因此 3 位可能就足够了（除了分辨率差的情况）。

我已经上传了 MUL 和 DIV 的两个组合实现。我仍然没有完全理解它们的工作原理，只是从我的 Digitalteknik 书籍中复制了原理图。我现在不明白的一件事是关于 Burk 的 x4+ 是什么。被除数 x 在值方面只有 4 位，那么其他位是什么？也许你在其余被除数 x/256 不存在时将它们设置为零。前四位表示 x/16 的数量，向右移四位得到 x/256。

我还得出了这样的结论：这种方法需要相当多的门。每个 FA/FS 由五个以上门组成，而 FA/FS 的数量大约为 20 个。

我将定义一个 FA/FS 只是为了好玩，它是一个相当简单而有效的模块。然而，在我的 CPU 中，我只设计了一个 FA（全加器），对于减法，我需要对数字进行反转并加上 1 再进行加法运算。这可以通过使用输入端的 XOR 门和将进位输入设置为 1 的组合 FA/FS 单元更容易实现。

然而，所示的 MUL 和 DIV 的组合解决方案相当快。使用早期的顺序解决方案，CPU 时钟将决定在 MUL/DIV 完成之前等待多长时间，这里我们只需要等待传播延迟。但是，CPU 时钟的周期必须大于传播延迟。

我的方法将类似于一个字节，如下所示

$x_{0}x_{1}x_{2}x_{3}y_{0}y_{1}y_{2}y_{3}$

对于乘法，x 是乘数，y 是被乘数；对于除法，x 是被除数，y 是除数，所有这些都是二进制补码。

乘法的结果将是

$p_{0}p_{1}p_{2}p_{3}p_{4}p_{5}p_{6}$

然而，它只有 7 位，但我计划将 p0 复制到 b7。

除法的结果将是

$r_{0}r_{1}r_{2}r_{3}q_{0}q_{1}q_{2}q_{3}$

它是 8 位。

那么问题是如何处理结果。

实际实现

在这里，我设计了一个称为 X 寄存器的预寄存器，这是因为结果需要一些（短暂的）时间才能有效，并且你必须保持输入，直到你能读取结果。此外，输入是两个 8 位寄存器，它们只能按顺序加载。

对于乘积 (p)，我将 p6 和 p7 缩短，以保持值对于正常的（8 位）取反完整；对于其余部分 (r) 和商 (q)，我将它们合并成一个字节，并将其余部分作为高 nibble，这是因为我们主要对商感兴趣，我们对结果字节进行 AND 0Fh 操作。因此，其余部分很特殊，因为它实际上有一个值为 1/64 的值，而商为 1/8。

可以在结果上运行 AND F0h 来获取其余部分，也许可以将它向右移四位以获得正确的值。我认为 4 位数的值部分（3 位）然后被缩放为 1/8。我对这一点非常不确定，但只要我们专注于商，就不会有问题。无论如何，其余部分都在那里。

如你所见，此解决方案需要 6 个额外的控制信号。现在我在我的原始 CPU 中使用 43 个控制信号。43+6=49，这超出了我的 6 个 27C512 EPROM 的处理能力，因此我思考了一段时间，我是否需要一个额外的 PROM（+ 8 个信号）。但看起来我并不需要它，因为我可以跳过一个信号（IE_D_FA）并使用 X 寄存器。目前，我设计了一个 8 位多路复用器，以使用存储在 FA 寄存器（LD_FA）中的扩展地址 HB，选择 A 总线（来自累加器）或 D 总线（来自内存）来“从上方”进入全加器 (FA)。对扩展操作码进行微编码意味着，在 PC 加 1 后，它将停留在地址（用于值）的高字节 (HB) 上，并且需要将此 HB 存储起来以备后用。到目前为止，我一直在使用 FA 寄存器来临时存储 HB。但是，这不是一个很好的解决方案，但我认为它可以工作。我认为一个更好的解决方案是使用我的新 X 寄存器。

但是，我将继续使用这个旧的解决方案（IE_D_FA）来进行我的 CPU 任务，因为我不想重新编译（除非出于其他原因必要）。好处是，当我实现 MUL/DIV 时，我可以省略多路复用器并使用我的 x 寄存器，因此我的 6 个 EPROM 就足够了。

我正在瞄准 MUL/DIV 的组合解决方案，因为我最喜欢它们。下一步将是设计一个组合的 FA/FS，我会尽快做到这一点。主要是在除法器中需要 FA/FS，但我计划在所有地方使用 FA/FS，因为这样可以简单地选择一直需要什么。如果你没有看到你需要什么类型，那就很尴尬了。使用组合的全加器 (FA) 和全减法器 (FS)，你只需在硬件中设置一个控制位。FA/FS 比单独的 FA/FS 更复杂一些，但我认为这是值得的。

我决定 X 寄存器将从 D 总线进入。这是因为这些值是从内存中输入的。使用所示的版本，我将不得不先加载累加器，然后才能将值放到 X 寄存器中。

我现在对此感到后悔，并将按照图纸进行，因为我有点喜欢我的 A 总线。通过累加器来输入 X 寄存器的值不会有什么麻烦。

我的计划是不使用超过 6 个 IR PROM，这意味着最多有 48 个数据引脚。现在我有 43 个引脚，上面的要求需要 6 个额外的引脚。因此，我将跳过读取高字节寄存器，只读取低字节寄存器。我认为这不是问题，因为我仍然可以充分利用一个额外的 8 位寄存器，我们可以称之为 X 寄存器。

FA/FS 组合

使用此单元，我们可以对二进制补码数字进行加法和减法运算。上面的全加器 (FA) 再次使用，但不是反转并加 1，我可以通过将 SUB 设置为高电平来做到这一点。关键是 XOR 门会反转 y，并且进位输入设置为 1（这意味着加 1）。因此，减法非常简单。

我将在我的 MUL/DIV 实现中使用这种方法，也许我甚至会更改框图（它已经缺少一个功能）。

体系结构缺陷

我得出的结论是，我的架构在处理 FA 时无法正常工作。问题似乎在于我有一个 H 标志（它不是真正的 H 标志），它嗅探来自顶部的操作数的符号位。我认为嗅探应该针对结果进行。也就是说，嗅探结果的 N 标志更好。让我们说明几个例子，第一个是向下翻滚（对于分支来说，所有这些都特别关键）。

假设 PC 的值为 FE02 (HBLB)，偏移量为 -4，那么我们从 LB 开始，像这样：

LB + (-4) = LB + 12

02
+
12
或
0000 0010
+
1111 1100
=
1111 1110, FE [-2 (2-4=-2)]

因此新的 LB 是正确的，但 HB 中的 E 必须减少，并且我们没有进位，那么该怎么做呢？我想到一个主意，如果结果的 b7 被设置（读取 N 标志），我们只需将 HB 加上 -1，这在偏移量仅为一个字节大时是可能的，因此我们只需要将 HB 的最低有效位向下计数一步。换句话说，我只用 ADD_HB+ADD_FF+C 将 FF 添加到 HB 中（当 N 被设置时）（C 在这里为零，但我认为我应该始终带有进位进行加法）。

让我们看一下向上翻滚，假设 HBLB 是 FDFE，而加的是 +4，那么我们有：

FE
+
04
或
1111 1
1111 1110
+
0000 0100
=
0000 0010, 02+进位

这里我们得到 02h，但带有进位，这并不奇怪，因为它意味着溢出，并且 HB 的最低位必须增加，这里我仅将 HB 加上进位 (ADD_HB+ADD_00+C)。到目前为止，我一直在嗅探我的特殊 H 标志（上操作数的符号），但我将把它改为嗅探结果。

如果我们现在看一下我们的中间结果，我们会发现如果符号位 (b7, N 标志) 被设置，我们应该加上 FF，如果没有被设置，我们应该加上 00。

我的加法器存在重大问题。我得出的结论是，我的版本根本无法正常工作，我正在努力弄清楚如何修复它。仅仅查看 N 标志并不起作用。我还实现了一个 V 标志，但我并不完全理解它（除了它嗅探两个最新的进位，即输出进位和之前的进位），但类似的东西可能有效。现在我认为 XOR 应该是一个反向 XOR，但我不知道。等我了解更多信息后会再联系你。

我想我现在知道该怎么做了，它比我想象的要简单。如果偏移量为负 (a7=my H=1)，则将 FF (-1) 加到高字节 (HB)，如果偏移量为正 (H=0)，则将 00 加到高字节。请注意，您还必须将 HB 加上进位，对此我有点不确定，但如果您看一下，如果我们使用 16 位 FA，进位始终存在。因此我们需要处理进位以使其正确。

查看我上面的解决方案，我唯一需要改变的是在两种情况下都强制执行 ADC（带进位加法）。这可以通过在尝试更改 HB (ADD_HB) 时在控制信号 ADC 旁边放置一个 OR 门来实现。

现在，我仍然不想重新编译（因为距离上次编译已经很久了），这意味着我将不得不跳过所有四个分支，集中验证其余部分。只要没有 HB 操作（即分支），我似乎能够使用 FA 来进行 INCA/DECA（递增/递减），因为这些仅仅是 "LB" 操作。

也许我还没有解决问题。如果您查看我上面的 FA/FS 电路，减一意味着偏移量完全反转，并且进位设置为高。我们希望将 HB 减一。那么偏移量一应该仅反转，并加上进位以使 HB 向下翻滚。如果我们加上 FF（和进位），我们加多了，可以这么说。我现在认为我们应该加上 FE，因为这是一的反转。然而，一个正常的数值将通过加上 FF 来递减，但在这里我们需要处理进位。

等等，在我上面的 FA/FS 中，进位被强制为减法的 1（偏移量仅反转）。但如果我们跳过进位的强制设置，HB 应该加上 FF。然而，在这里我们知道我们想要减法。我得再想想这件事。

我想我现在明白了。当偏移量的 a7 被设置时，你将 HB（PC 的 HB）加上偏移量的二进制补码。这意味着你只需将 ADD_FF 和 HB 以及进位一起运行。如果偏移量的 a7 为零，则将 ADD_00 和 HB 以及进位一起运行。因此，我唯一遗漏的是加上进位。在我上面的原理图中，加上进位似乎不起作用，但我仍然可以将控制信号 ADC 设置为 1 以加上前一个进位。因此，我不需要重新编译，我仍然可以实现分支！

我将一步一步地进行，使用我当前的架构。虽然我使用 43 个控制信号，我的 MUL/DIV 解决方案需要 6 个额外的控制信号，但看起来我需要另一个 27C512。但是，当/如果我实现 MUL/DIV 时，我可以省略信号 IE_D_FA，因为该信号只是在那里用于启用 A 总线或 D 总线从上面进入 FA。双总线在您临时希望存储例如 PC 的高字节以进行分支跳转时非常有用，并且没有其他地方可以存储 PCHB（它首先出现在程序内存中）。然而，如果我在 MUL/DIV 中实现一个 X 寄存器，我可以将 PCHB 存储在那里，而 IE_D_FA 就会变得过时。因此，我认为我会继续使用仅 6 块 27C512。

缺点是，如果我使用 IE_D_FA 对指令进行微编码，那么当/如果我决定实现 X 寄存器时，我将不得不重新编程微编码，但我认为这不是什么大问题，我更高兴的是我找到了一个不用重新编译就能实现分支的方法。

CPU 测试程序（伪汇编程序）

让我们从编程 $8000 的复位向量开始，这是我们的程序开始的地方。因此，我们在 $FFFE 中编程 $80，在 $FFFF 中编程 $00。当为我们的 CPU 通电时，起始地址为 $FFFE，它存储着 $80，然后读取 $80，使用我们的 DC 时钟 (SW2)，我们最终得到 $FFFF，并读取 $00，这使得我们的起始地址变为 $8000。在这里，第一个操作码 (LDA 或 $A6) 被读取，再次使用 SW2 使它的操作数 #$FE 被读取。我认为我会省略所有立即数值之前的 # 符号，因为很明显它是一个立即数值（仅一个字节）。然而，$ 符号告诉我们该数值是十六进制的。但我也在地址之前使用 $（它们也是十六进制的），因此纯 $ 可能适合扩展寻址（RAM 或 I/O），而立即寻址（属于程序内存）之前的一个字节的 $ 之前可能适合 #。

我们现在将尝试编写一个程序，根据上面 CPU 助记符一章中描述的 33 条指令进行测试，因此我们从起始地址 $8000 开始。然后，一个测试程序可能看起来像下面这样，我们为所有指令添加了绝对地址，通常不会这样做，因为程序可以放置在内存中的任何位置（并且由链接器完成，我认为）。由于教学原因，我们选择了绝对地址。

我们的内存映射告诉我们，$4000 位于 I/O 区域内，因此我们可以对同一个地址进行读写。由于我们选择的内存映射，不可能有鼠标。

请注意，可以使用 HCS08 编译器编写更复杂的程序。

我的程序仅适用于 “DC 时钟”，在实际情况下必须有循环，但我只想验证指令（其中 LDS/NOTA 已被省略）。

$8000 LDA #$FE //-2
$8002 ADD #$02 //A 中的值现在为 $00，但已产生进位
$8004 ADC #$00 //带有进位加法
$8006 STA $4000 //$01 在 I/O 输出
$8009 LDA $4000 //用 HEX-sw 设置 $FE
$800C ADD $4000 //用 HEX-sw 设置 $02
$800F ADC $4000 //用 HEX-sw 设置 $00
$8012 STA $4000 //$01 在 I/O 输出
$8015 LDA #$FE //-2
$8017 DECA //递减一步
$8018 CMP #$FC
$801A BNE $FC //(-4)，这将执行两次
$801C STA $4000 //$FC 在 I/O 输出
$801F INCA //递增一步
$8020 CMP $4000 //设置 $FF
$8023 BNE $FB //(-5)，这将执行两次
$8025 CMP #$FF
$8027 BEQ $01 //下一条指令
$8029 LDA #$00
$802B CMP #$01
$802D BMI $01 //A-M<0，下一条指令
$802F LDA #$02
$8031 CMP #$01
$8033 BPL $01 //A-M>0，下一条指令
$8035 LDA #$01
$8037 EOR #$F0 //$01 XOR $F0=$F1
$8039 STA $4000 //$F1 在 I/O 输出
$803C EOR $4000 //设置 $01
$803F STA $4000 //$F0 在 I/O 输出
$8042 JSR $9000 //这是一个子程序
$8045 LDA #$02
$8047 LSRA
$8048 STA $4000 //$01 在 I/O 输出
$804B LSLA
$804C STA $4000 //$02 在 I/O 输出
$804F LDA #$01
$8051 NEGA
$8052 STA $4000 //$FF 在 I/O 输出
$8055 NOP //无操作
$8056 LDA #$F2
$8058 ORA #$F3
$805A STA $4000 //$F3 在 I/O 输出
$805D ORA $4000 //设置 $F4
$8060 STA $4000 //$F7 在输出
$8063 PSHA
$8064 PULA
$8065 STA $4000 //$F7 再次在 I/O 输出
$8068 SUB $4000 //设置 $FF
$806B STA $4000 //$F6 在 I/O 输出
$806E SUB #$FF
$8070 STA $4000 //$F5 在 I/O 输出
$8073 LDA #$01
$8075 ADD #$01 //没有设置标志
$8077 TPA //CCR->A
$8078 STA $4000 //C、V、Z、N 和 H 应该都为零（即 b7-b3），输出为 $00
$807B LDA #$0F
$807D AND #$02
$807F STA $4000 //$02 在 I/O 输出
$8082 AND $4000 //设置 $F2
$8085 STA $4000 //$02 在 I/O 输出
$8088 JMP $8000 //从头开始

$9000 RTS //在这个地址，我们暂时只编程 RTS 的操作码，即子程序返回

$FFFE $80
$FFFF $00 //在这里，我们编程重置向量，它指向程序开始的位置

我在这里列出测试的指令
1) LDA #, $
2) ADD #, $
3) ADC #, $
4) STA
5) DECA
6) CMP #, $
7) BNE
8) INCA
9) BEQ
10) BMI
11) BPL
12) EOR #, $
13) JSR
14) LSRA
15) LSLA
16) NEGA
17) NOP
18) ORA #, $
19) PSHA
20) PULA
21) SUB #, $
22) TPA
23) AND #, $
24) JMP
25) RTS

这个列表有 25 条指令，但我还测试了立即数和扩展指令，因此实际测试指令的数量似乎为 33。我在上面的助记符映射中计算了 33 条指令。

CPU 测试程序（汇编程序）

在这里，我们指定程序存储器中每个地址的地址应该发生什么。我们使用纯十六进制代码（不再使用 $ 符号），并省略助记符，但将其保留为注释，以便跟踪发生了什么。我添加了如何使用十六进制开关（或键盘）进行设置，以及在显示屏上应该显示什么。这样，该程序就可以打印出来，并在我们的 CPU 运行时查看。

8000 A6 //LDA #
8001 FE
8002 AB //ADD #
8003 02
8004 A9 //ADC #
8005 00
8006 C7 //STA $, 01 输出
8007 40
8008 00
8009 C6 //LDA $, 设置 FE
800A 40
800B 00
800C CB //ADD $, 设置 02
800D 40
800E 00
800F C9 //ADC $, 设置 00
8010 40
8011 00
8012 C7 //STA $, 01 输出
8013 40
8014 00
8015 A6 //LDA #
8016 FE
8017 4A //DECA
8018 A1 //CMP #
8019 FC
801A 26 //BNE
801B FC //(-4)
801C C7 //STA $, 1C 输出
801D 40
801E 00
801F 4C //INCA
8020 C1 //CMP $, 设置 FF
8021 40
8022 00
8023 26 //BNE
8024 FB //(-5)
8025 A1 CMP #
8026 FF
8027 27 //BEQ
8028 01
8029 A6 //LDA #
802A 00
802B A1 //CMP #
802C 01
802D 2B //BMI
802E 01
802F A6 //LDA #
8030 02
8031 A1 //CMP #
8032 01
8033 2A //BPL
8034 01
8035 A6 //LDA #
8036 01
8037 A8 //EOR #
8038 F0
8039 C7 //STA $, F1 输出
803A 40
803B 00
803C C8 //EOR $, 设置 01
803D 40
803E 00
803F C7 //STA $, F0 输出
8040 40
8041 00
8042 CD //JSR $
8043 90
8044 00
8045 A6 //LDA #
8046 02
8047 44 //LSRA
8048 C7 //STA $, 01 输出
8049 40
804A 00
804B 48 //LSLA
804C C7 //STA $, 02 输出
804D 40
804E 00
804F A6 //LDA #
8050 01
8051 40 //NEGA
8052 C7 //STA $, FF 输出
8053 40
8054 00
8055 9D //NOP
8056 A6 //LDA #
8057 F2
8058 AA //ORA #
8059 F3
805A C7 //STA $, F3 输出
805B 40
805C 00
805D CA //ORA $, 设置 F4
805E 40
805F 00
8060 C7 //STA $, F7 输出
8061 40
8062 00
8063 87 //PSHA
8064 86 //PULA
8065 C7 //STA $, F7 输出
8066 40
8067 00
8068 C0 //SUB $, 设置 FF
8069 40
806A 00
806B C7 //STA $, F6 输出
806C 40
806D 00
806E A0 //SUB #
806F FF
8070 C7 //STA $, FE 输出
8071 40
8072 00
8073 A6 //LDA #
8074 01
8075 AB //ADD #
8076 01
8077 85 //TPA
8078 C7 //STA $, 00 输出
8079 40
807A 00
807B A6 //LDA #
807C 0F
807D A4 //AND #
807E 02
807F C7 //STA $, 02 输出
8080 40
8081 00
8082 C4 //AND $, 设置 F2
8083 40
8084 00
8085 C7 //STA $, 02 输出
8086 40
8087 00
8088 CC //JMP $
8089 80
808A 00

9000 81 //RTS

FFFE 80
FFFF 00

CPU 测试程序（可刻录的纯机器码）

在这里，我们列出了上述程序，以便 PROM 刻录器可以使用。每行/地址包含 8 个字节。

8000 A6 FE AB 02 A9 00 C7 40
8008 00 C6 40 00 CB 40 00 C9
8010 40 00 C7 40 00 A6 FE 4A
8018 A1 FC 26 FC C7 40 00 4C
8020 C1 40 00 26 FB A1 FF 27
8028 01 A6 00 A1 01 2B 01 A6
8030 02 A1 01 2A 01 A6 01 A8
8038 F0 C7 40 00 C8 40 00 C7
8040 40 00 CD 90 00 A6 02 44
8048 C7 40 00 48 C7 40 00 A6
8050 01 40 C7 40 00 9D A6 F2
8058 AA F3 C7 40 00 CA 40 00
8060 C7 40 00 87 86 C7 40 00
8068 C0 40 00 C7 40 00 A0 FF
8070 C7 40 00 A6 01 AB 01 85
8078 C7 40 00 A6 0F A4 02 C7
8080 40 00 C4 40 00 C7 40 00
8088 CC 80 00 FF FF FF FF FF

9000 81 FF FF FF FF FF FF FF

FFF8 FF FF FF FF FF FF 80 00

未编程地址中的数据通常为 FF。为了清晰起见，我添加了 FF 以使行看起来更好。

CPU 测试程序（s 记录）

这里我 Dataman S4 刻录器的语法是
地址、校验和、要刻录的字节
校验和实际上很简单，它似乎只是字节的计数（包括校验和）。在这里，我列出了每行/地址 8 个字节的数据，因此每行的校验和相同，但在实践中并非如此（见下文）。

S1 0B 80 00 A6 FE AB 02 A9 00 C7 40
S1 0B 80 08 00 C6 40 00 CB 40 00 C9
S1 0B 80 10 40 00 C7 40 00 A6 FE 4A
S1 0B 80 18 A1 FC 26 FC C7 40 00 4C
S1 0B 80 20 C1 40 00 26 FB A1 FF 27
S1 0B 80 28 01 A6 00 A1 01 2B 01 A6
S1 0B 80 30 02 A1 01 2A 01 A6 01 A8
S1 0B 80 38 F0 C7 40 00 C8 40 00 C7
S1 0B 80 40 40 00 CD 90 00 A6 02 44
S1 0B 80 48 C7 40 00 48 C7 40 00 A6
S1 0B 80 50 01 40 C7 40 00 9D A6 F2
S1 0B 80 58 AA F3 C7 40 00 CA 40 00
S1 0B 80 60 C7 40 00 87 86 C7 40 00
S1 0B 80 68 C0 40 00 C7 40 00 A0 FF
S1 0B 80 70 C7 40 00 A6 01 AB 01 85
S1 0B 80 78 C7 40 00 A6 0F A4 02 C7
S1 0B 80 80 40 00 C4 40 00 C7 40 00
S1 0B 80 88 CC 80 00 FF FF FF FF FF

S1 0B 90 00 81 FF FF FF FF FF FF FF

S1 0B FF F8 FF FF FF FF FF FF 80 00

CPU 测试程序（一次一条指令）

我希望一次测试一条指令，而不是多个 EPROM（或重新编程），我们可以使用一个 EPROM，但需要像这样进行编程

LDA $I/O [将 I/O 地址输入上的值加载到累加器 A 中，我将此行和地址定义为“开始”]

CMP $#00 [将该值与 00h 进行比较，需要将其设置为继续]

BNE -6 [只要 I/O 不是 00h，它就会重复/等待，预计跳转地址的 LB 将使其退出循环]

PSHA [跳转地址的低字节（LB）被压入堆栈，以便稍后获取]

LDA $I/O [设置 00h 以进行参考，否则该值为 LB]

CMP $#00 [检查该值是否为 00h]

BNE -6 [当该值不为 00h 时，它会重复]

LDA $I/O [设置跳转地址的 HB，I/O 现在处于 00h]

CMP $#00 [检查该值是否为 00h]

BEQ -6 [当该值不为 00h 时，它将继续执行并将存储在 A 中的“正确”HB 用于跳转地址]

PSHA [跳转地址的高字节（HB）被压入堆栈]

RTS [从堆栈中拉出 HBLB，并使 PC=HBLB]

在子程序中，你只需使用 JMP $start 结束，然后重复所有操作。下次，你将输入另一个 HBLB，程序计数器（PC）将跳到该地址，该地址是新子程序/程序的开头。输入正确的 HBLB 至关重要，因为否则我们将跳到没有程序（因此没有 JMP）的地址区域。但是，在这种情况下，我们只需打开和关闭电源即可。

等待循环没有必要，因为我们有一个以外部时钟形式的“进入”。因此，外部值仅在按下回车键时才被锁存到 CPU 中，然后 CPU 只要有时间就会读取锁存的值。但是，我将保留此程序，因为它很有趣，它说明了如何在外部 I/O 值的帮助下设置新的 CP 值。

另一个小问题是，我们需要在测试指令之前测试所有这里使用的指令。因此，此程序被丢弃，我将使用尽可能少的指令的程序，从原始测试程序开始。

CPU 测试程序（原始）

在这里，我列出了原始测试程序，其中至少 JMP 指令可以正常工作。

$9000 LDA$ //C6
$9003 CMP# //A1
$9005 BNE //26
$9007 STA$ //C7
$900A LDA$ //C6
$900D CMP# //A1
$900F BNE //26
$9011 STA$ //C7
$9014 JMP$ //CC

我只能在这里猜测，因为我没有完整的程序，但也许

$9000 LDA$ $4000，设置 $01 [测试数据总线的读取部分]
$9003 CMP# $01 [测试全加器 FA 的减法部分]
$9005 BNE -6 或 $FA [测试分支是否有效，以及 PC 是否可以相应地更改]
$9007 STA $4000，$01 输出 [测试地址总线的写入部分]
$900A JMP $9000 [测试 PC 是否可以更改]

我在这里对程序进行了简化，旨在突出最重要的部分，S 记录为

S1 06 90 00 C6 40 00
S1 06 90 03 A1 01 FF
S1 06 90 05 26 01 FF
S1 06 90 07 C7 40 00
S1 06 90 0A CC 40 00

微指令编程示例

为我们的 CPU 编程微指令的方式如下：如果我们查看第一个 EPROM (M0) 以及仅 RST 指令，它可能会像这样编程

0000 00
0001 00
0002 00
0003 00
0004 00
0005 00
0006 00
0007 01

或作为 S 记录
S1 0B 00 00 00 00 00 00 00 00 00 01

为了比较，ADC# 可以像这样编程
A900 00
A901 00
A902 00
A903 88
A904 00
A905 01

或作为 S 记录
S1 09 A9 00 00 00 00 88 00 01

然后，IR EPROM 的编程可以压缩为（编程两个指令）
S1 0B 00 00 00 00 00 00 00 00 00 01
S1 09 A9 00 00 00 00 88 00 01

我不喜欢不同的校验和，因此在实践中，这会导致
S1 0B 00 00 00 00 00 00 00 00 00 01
S1 0B A9 00 00 00 00 88 00 01 FF FF

其中我用 FF 填充了最后两个字节（如同在未编程的单元格中）。

CPU 灵感

CPU（中央处理器）是计算机的大脑。然而，指令寄存器（IR）是 CPU 内部的“大脑”。没有 IR（或图中的 ROM），就不可能解释或执行指令。指令也必须以预定义的形式出现，否则“大脑”会迷路。有趣的是，这里实际上存在两种“大脑”。也许你可以将 CPU 称为“大腦”，将指令寄存器称为“小腦”？

基本 CPU

这幅图显示了最简单的机器，它可以代表一个非常简单的 CPU（实际上是我的灵感来源，据说它代表一台洗衣机），内部指令（操作码或 OP-kod）在这里得以实现。数据输出实际上可以控制要做什么以及按什么顺序。该机器使用分页内存，这意味着每个操作码或指令都被分配了一个特定的内存区域以供遍历。这是因为计数器（Räknare）遍历 IR 地址的低位。我在上面将这个计数器称为 IRC，代表指令寄存器计数器。“Klar”表示准备就绪。

现代 CPU

这幅图显示了一个比较现代的 CPU 的架构。它包含一个用于算术和逻辑运算的单元，称为 ALU（算术逻辑单元），一个累加器（AC），一个程序计数器（PC），一个数据寄存器（DR），一个地址寄存器（AR）和一个指令寄存器（IR），以及一些控制信号。

结语

以上是对理解和设计 CPU 的尝试。并非总是能够完全理解，因此我经常在尝试理解的过程中偏离方向。随着时间的推移，某些事情变得清晰起来，为本书提供了一些结构。就目前的感觉而言，存在很少的差异。现在存在的差异是那些考虑微指令编码的差异。我认为第一次尝试让他们工作起来相当困难。

尝试写下我所知道、所思以及有时所相信的东西非常有趣。唯一有点令人悲伤的是所有这些闲聊，但我感觉我既没有动力也没有想要对此做些什么。很大程度上是因为它是开发和自学的一部分。

来源

http://www.freescale.com/files/microcontrollers/doc/ref_manual/HCS08RMV1.pdf
Per-Erik Danielsson，Lennart Bengtsson，Digital Teknik，第三版，1986 年，瑞典
John P. Hayes，计算机体系结构与组织，第二版，1988 年，新加坡