元胞自动机/列出原像

本文描述了两种用于列出当前配置的原像的算法。第一个算法在 Andrew Wuensche 的许多文本中都有描述，第二个算法是本书中介绍的。

原像网络

为了便于根据图中路径描述反向算法，引入了新的图，即原像网络。

单个单元格的原像图是该单元格的原像网络。就像序列中单元格的原像矩阵 $\alpha =c_{0},c_{1},\dots ,c_{x},\dots ,c_{l-1}$ 长度 $l$ 对齐成一条链并相乘，每个单元格的原像图可以对齐形成原像网络。如果考虑了 De Bruijn 图中的所有链接，那么只有那些映射到观察到的单元格的邻域的链接才是有效链接。图中节点之间的每个链接或路径，由许多链接组成，都是一个局部有效路径。

元素 $d_{o_{L}o_{R}}$ 在相乘的原像矩阵 $D(\alpha )$ 中统计从左侧重叠之一 $o_{L}=o_{0}$ 开始，并以右侧重叠之一 $o_{L}=o_{l}$ 结束的原像数。同理，原像网络中两个重叠之间有 $d_{o_{L}o_{R}}$ 条不同的有效路径。

全局有效的定义取决于有限格是有界还是循环。

在有界格上，全局有效路径连接左侧边界上的任何重叠到右侧边界上的任何重叠。
在循环格上，全局有效路径必须始于并止于相同的重叠值。

局部有效路径上的节点是局部有效节点。全局有效路径上的节点是全局有效节点。

指向链接以增加位置索引方向的箭头可以省略。

链接权重

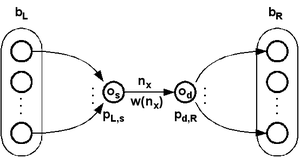
原像网络中的重叠和邻域可以根据通过它们的全局有效路径的数量进行加权。权重可以在原像网络上以节点大小（在示例中未使用）和线粗细来表示。由于原像的数量可能呈指数级增长，因此粗细可能是权重的对数。

w_{log}=\log _{|S|}w

取决于有限格是有界还是循环，有两种不同的方法来定义和计算权重。

有界格

链接 $n_{x}=o_{s}c_{s}=c_{d}o_{d}$ 在位置索引 $x$ 的权重是

从左边界 $b_{L}$ 到源重叠 $o_{s}$ 的路径数量 $p_{b_{L},o_{s}}$ 和
从排水重叠 $o_{d}$ 到右边界 $b_{R}$ 的路径数量 $p_{o_{d},b_{R}}$ 的乘积。

w(n_{x})=p_{b_{L},0_{s}}\cdot p_{o_{d},b_{R}}

乘积的两个部分都包含在原像向量中，左侧为 $b_{s}$ ，右侧为 $b_{d}$ 。

b_{s}=b_{L,x}=b_{L}D(c_{0}c_{1}\dots c_{x-1})

b_{d}=b_{x+1,R}=D(c_{x+1}c_{x+2}\dots c_{l-1})b_{R}

循环格

在循环格上，链接 $n_{x}=o_{s}c_{s}=c_{d}o_{d}$ 在位置索引 $x$ 的权重是重叠的乘积之和。

从一个左侧重叠 $o_{L}$ 到源重叠 $o_{s}$ 的路径数 $p_{o_{L},o_{s}}$ ，以及
从排水重叠 $o_{d}$ 到右侧边界 $b_{R}$ 的路径数 $p_{o_{d},o_{R}}$ 。

w(n_{x})=\sum _{o=0}^{|S|^{k-1}-1}p_{o,o_{s}}\cdot p_{o_{d},o}

由于边界重叠必须区分，因此原像向量是不够的，路径数量的信息包含在原像矩阵中。

D_{L,x-1}(c_{0}c_{1}\dots c_{x-1})\qquad D_{x+1,R}(c_{x+1}c_{x+2}\dots c_{l-1})

计算权重

为了计算所有连接权重，需要从左侧边界到每个单元格的原像计数，以及从右侧边界到每个单元格的原像计数。对于有界格，计数存储在原像向量中，对于循环格，计数存储在原像矩阵中。

有界格

对于有界格，原像计数存储为原像向量。左侧第一个计数为 $b_{L,0}$ ，右侧第一个计数为 $b_{l,R}$ ，它们是边界向量。

b_{L,0}=b_{L}\qquad b_{l,R}=b_{R}^{T}

左侧计数 $b_{L,x}$ 是从左到右计算的，位置 $x$ 的向量是由位置 $x-1$ 的向量计算得来的。右侧计数 $b_{x,R}$ 是从右到左计算的，位置 $x$ 的向量是由位置 $x+1$ 的向量计算得来的。

b_{L,x}=D(c_{0}c_{1}\dots c_{x-1})b_{R}^{T}=b_{L,x-1}D(c_{x-1})

b_{x,R}=D(c_{x}c_{x+1}\dots c_{l-1})b_{R}^{T}=D(c_{x})b_{x+1}

所有原像的总数是通过应用两个边界计算得出的。

p=b_{L}D(\alpha )b_{R}^{T}=b_{L}b_{0,R}=b_{L,l}b_{R}^{T}

从左到右计数的算法伪代码

b[0] = b_L                     # the left preimage vector b[0] is initialized to the left boundary b_L
for ( x=1; x<=l; x++ )         # run the position index from the left (x=0) to the right (x=l-1)
  b[x] = b[x-1]*D[C[x-1]]      # the new preimage vector is calculated from the old using the
end                            # preimage matrix D[C[x-1]] of the cell value C[x-1] at position x-1

p = 0                          #
for ( o=0; o<|S|^(k-1); o++ )  # the number of all preimages p is the scalar product of
  p += b[l][o] * b_R[o]        # the last right preimage vector b[l] and the right boundary vector b_R
end                            #

从右到左计数的算法伪代码

b[l] = b_R                     # the right preimage vector b[l] is initialized to the right boundary b_R
for ( x=l-1; x>=0; x-- )       # run the position index from the right (x=l-1) to the left (x=0)
  b[x] = D[C[x]]*b[x+1]        # the new preimage vector is calculated from the old using the
end                            # preimage matrix D[C[x]] of the cell value C[x] at position x

p = 0                          #
for ( o=0; o<|S|^(k-1); o++ )  # the number of all preimages p is the scalar product of
  p += b_L[o] * b[0][o]        # the last left preimage vector b[0] and the left boundary vector b_L
end                            #

示例:

规则 110 中两个序列的原像图

循环格

对于循环格，计数被存储为原像矩阵，这对于区分连接边界处每个重叠的计数是必要的。由于格是循环的，因此不需要像在有界格中那样应用边界向量。

左侧计数 $D_{L,x}$ 是从左到右计算的，位置 $x$ 的矩阵是由位置 $x-1$ 的矩阵计算得来的。右侧计数 $D_{x,R}$ 是从右到左计算的，位置 $x$ 的矩阵是由位置 $x+1$ 的矩阵计算得来的。

D_{L,x}=D(c_{0}c_{1}\dots c_{x-1})=D_{L,x-1}D(c_{x-1})

D_{x,R}=D(c_{x}c_{x+1}\dots c_{l-1})=D(c_{x})D_{x+1,R}

在每个连接边界处的 $|S|^{k-1}$ 重叠处，必须分别统计原像的数量 $o_{L}=o_{0}=o_{l}=o_{R}$ 。一个循环原像（行）向量 $b_{\circ }(\alpha )$ 是根据原像矩阵 $D(\alpha )$ 的对角元素构建的。

D(\alpha )=D_{0,R}=D_{L,l-1}

b_{\circ }(\alpha )=\left[d_{0,0}(\alpha ),d_{1,1}(\alpha ),\dots ,d_{|S|^{k-1},|S|^{k-1}}(\alpha )\right]

所有原像的总数是循环原像向量 $b_{\circ }(\alpha )$ （行）中元素的总和，即与无限制边界向量 $b_{u}$ （行转置为列）的标量积。

p=b_{\circ }(\alpha )b_{u}^{T}

从左到右计数的算法伪代码

D[0] = I                       # the left preimage matrix D[0] is initialized to the identity matrix
for ( x=1; x<l; x++ )          # run the position index from the left (x=0) to the right (x=l-1)
  D[x] = b[x-1]*D[C[x]]        # the new preimage matrix is calculated from the old using the
end                            # preimage matrix D[C[x]] of the cell value C[x] at position x

p = 0                          #
for ( o=0; o<|S|^(k-1); o++ )  # the number of all preimages p is the scalar product of
  p += D[l-1][o][o]              # the sum of the diagonal elements of the right preimage matrix D(l-1)
  b_0[o] = D[0][o][o]          # the diagonal are copied into the cyclic preimage vector b_0
end                            #

从右到左计数的算法伪代码

D[l] = I                       # the right preimage matrix D[l] is initialized to the identity matrix
for ( x=l-1; x>=0; x-- )       # run the position index from the right (x=l-1) to the left (x=0)
  D[x] = D[C[x]]*b[x+1]        # the new preimage matrix is calculated from the old using the
end                            # preimage matrix D[C[x]] of the cell value C[x] at position x

p = 0                          #
for ( o=0; o<|S|^(k-1); o++ )  # the number of all preimages p is the scalar product of
  p += D[0][o][o]              # the sum of the diagonal elements of the left preimage matrix D(0)
  b_0[o] = D[0][o][o]          # the diagonal are copied into the cyclic preimage vector b_0
end                            #

示例:

规则 110 中两个序列的原像图

字符串操作

原像网络中的路径用邻域和重叠来描述，它们都是细胞序列。由于全局有效路径上的邻域相互重叠，每个细胞可以在 $k$ 个邻域中找到，也可以在 $k$ 个重叠中找到。

邻域用原像图和网络中的链接表示。围绕细胞 $c_{x}$ 的邻域 $n_{x}$ 定义为

n_{x}=c_{x-k_{0}}c_{x-k_{0}+1}\dots c_{x}\dots c_{x+k-k_{0}-1}

在原像图和网络中，重叠用节点表示。包围单元格 $c_{x}$ 的重叠 $o_{x}$ 定义为：

o_{x}=c_{x+1-k_{0}}c_{x+2-k_{0}}\dots c_{x}\dots c_{x+k-k_{0}-1}

序列可以通过两种方式表示和操作：

紧凑表示使用代数运算（乘法、除法（无余数商）和模运算）进行操作
位数组使用布尔逻辑运算（移位、与 OR 融合和与 AND 掩码）进行操作，每个单元格消耗 $m=top(\log _{2}|S|)$

提取观察到的单元格

从邻域提取

代数表示法

c_{x}=n_{x}/|S|^{k-k_{0}-1}\mod |S|

逻辑表示法

c_x = (n_x >> m*(k-k_0-1)) AND (2^m-1)

从重叠提取

代数表示法

c_{x}=o_{x}/|S|^{k-k_{0}}\mod |S|

逻辑表示法

c_x = (o_x >> m*(k-k_0)) AND (2^m-1)

重叠和邻域之间的转换

将重叠扩展为邻域

一个邻域 $n$ （长度 $k$ ）是由一个重叠 $o$ （长度 $k-1$ ）通过在左侧或右侧添加一个单元格 $c$ 创建的。

字符串表示法（单元格字符串的连接）

n_{x}=o_{x}c_{x+k-k_{0}-1}

n_{x-1}=c_{x-k_{0}-1}o_{x}

代数表示法

n_{x}=o_{x}\cdot |S|+c_{x+k-k_{0}-1}

n_{x-1}=c_{x-k_{0}-1}\cdot |S|^{k-1}+o_{x}

逻辑表示法

n_x = (o_x << m) OR c

n_x-1 = (c << m(k-1)) OR o_x

将邻域缩短为重叠

一个重叠 $o$ （长度 $k-1$ ）是由一个邻域 $n$ （长度 $k$ ）通过在左侧或右侧删除一个单元格 $c$ 创建的。

字符串表示法

$\alpha \,/\,a$ 表示字符串 $\alpha$ 去掉最右侧符号 $a$
$b\setminus \beta$ 表示字符串 $\beta$ 去掉最左侧符号 $b$ )

o_{x}=n_{x}\,/\,c_{x+k-k_{0}-1}\quad \Rightarrow \quad n_{x}=o_{x}c_{x+k-k_{0}-1}

o_{x+1}=c_{x-k_{0}}\setminus n_{x}\quad \Rightarrow \quad n_{x}=c_{x-k_{0}}o_{x+1}

代数表示法

o_{x}=n_{x}/|S|

o_{x+1}=n_{x}mod|S|^{k-1}

逻辑表示法

n_x = o_x >> m

n_x+1 = o_x AND (2^(m*(k-1))-1)

追踪和回溯算法

该算法通过原像图追踪路径。它从最左侧未被左侧边界条件遮挡的第一个节点开始。根据位置索引值以及是否存在右侧连接，有四种选择

追踪第一个未被使用的有效连接到下一个节点，并记录所选路径
如果到达的节点在右侧边界，则测试边界的有效性，并将路径存储为原像
如果没有未被使用的右侧连接，则回溯到当前路径上的前一个节点
当回溯到达左侧边界时，追踪从下一个有效节点重新开始，直到所有节点都已遍历。

该算法可以从右侧开始，向左追踪，获得相同的原像。方向追踪的选取方式是为了让列出的原像按其紧凑表示的升序排序。

形式化算法描述

该算法的大部分内容在有界和循环格子上是相同的，只有在边界处有所不同。

主循环和左侧边界

主循环遍历可用的追踪起点。该算法从左侧的第一个重叠开始追踪 $o=o_{L}=0$ （在有界格子上，被左侧边界遮挡的重叠 $b_{L}$ 会被跳过）。当所有从该重叠开始的追踪都已遍历（回溯到达左侧边界 $x=0$ 并且连接索引超过可用连接的数量 $c=|S|$ ）时，追踪将继续到下一个有效重叠 $o_{L}=o_{L}+1$ ，直到到达最后一个重叠 $o_{L}=|S|^{k-1}-1$ 。当最后一个重叠的追踪都已遍历时，算法结束。在有界格子上，重叠可能是无限制的，也可能是被边界向量 $b_{L}$ 遮挡的。在循环格子上，所有重叠都被使用。

追踪

跟踪会增加当前位置索引 $x=x+1$ 。每次跟踪步骤都从当前重叠 $o_{x}$ 开始，该重叠位于位置 $x$ ，并跟踪第一个尚未被跟踪的链接到排水重叠 $o_{d}$ ，该重叠位于位置索引 $x+1$ 。需要跟踪 $|S|$ 个链接，如果当前重叠尚未回溯，则跟踪从链接 $c=0$ 开始，否则回溯提供的链接会被递增。必须验证跟踪步骤的有效性，每个链接都代表一个邻域 $n=o_{s}c$ ，该邻域必须指向当前单元格的值 $f(n_{x}^{t-1})=c_{x}^{t}$ 。

如果链接有效，则其索引 $c$ 会被存储为当前跟踪路径上的一个新单元格 $c_{x+k-k_{0}-1}=c$ ，算法将从排水节点 $o_{d}=c_{x-k_{0}}\setminus o_{x}c_{x+k-k_{0}-1}$ 继续。
如果链接无效，则跟踪必须继续进行下一个链接 $c=c+1$ ，如果没有剩余链接 $c=|S|$ ，则算法将切换到回溯。

回溯

回溯是指在当前路径上返回，直到找到可用于跟踪的可用链接。当前没有进一步路径的重叠是 $o_{x}$ ，每次回溯步骤都沿着当前路径上的链接 $n_{x-1}$ 向后移动到位置索引 $x-1$ 处的重叠 $o_{s}$ 。向后的链接 $n_{x-1}=c_{x-k_{0}-1}o_{x}$ 和源重叠 $n_{x-1}=c_{x-k_{0}-1}o_{x}\;/\;c_{x+k-k_{0}-2}$ 是当前路径上的序列。当回到源单元格时，向前跟踪的链接从最后一个跟踪的链接 $c=c_{x+k-k_{0}-2}+1$ 递增。

右边界和原像列表

当跟踪到达右边界时，列出原像可以开始。

对于循环格，当前重叠 $o_{x}$ 与左侧的起始重叠 $o_{L}$ 进行比较，如果它们相等，则将长度为 $l$ 的原像 $C^{t-1}=c_{0}c_{1}\dots c_{l-1}$ 添加到原像列表中。
对于有界格，当前重叠 $o_{x}$ 被右边界向量 $b_{R}$ 掩盖，如果被接受，则将长度为 $l+k-1$ 的原像 $C^{t-1}=c_{-k_{0}}\dots c_{l+k-k_{0}-1}$ 添加到原像列表中。

对于每个新的原像，原像计数器 $p$ 递增。

算法伪代码

p=0                               # the preimage counter is initialized to 0
x=0                               # the position index is initialized to 0
c=0                               # the link index is initialized to 0
o_L=0                             # the tracing starts at the first left overlap
while (bounded) then              # if the lattice is bounded
  if ( b[o_L]>0 ) then            # boundary conditions must be checked
    o_L++                         # to ensure the start point is valid
  end_if                          #
end_while                         #
o=o_L                             # the current overlap is initialized

while (o_L<|S|^(k-1)) then        ## main loop ##

if ( c<|S| ) then                 # tracing and right boundary

  if ( x<l ) then                 ## tracing ##
    n=o*|S|+c                     # the neighborhood is created
    if ( f(n)==c_x ) then         # checking it the neighborhood is valid
      o=(o*|S|+c)/|S|^k           # stepping to the new overlap at the right
      C[x+k-k0-1]=c               # storing the link selection cell
      x++                         # incrementing the position index
      c=0                         # at the new overlap start with the first link
    else                          # the selected link is not valid
      c++                         # try the next link
    end_if                        #
  end_if                          #

  else                            ## right and cyclic boundary conditions ##
    if (bounded)                  # for bounded lattices
      if ( b[o]>0 ) then          # check masking of the current overlap with the right boundary vector
        store(C)                  # list the preimage consisting of cells on the current path
      end_if                      #
    end_if                        #
    if (cyclic)                   # for cyclic lattices
      if ( o==o_L ) then          # check if overlaps at the left and right boundary are equal
        store(C)                  # list the preimage consisting of cells on the current path
      end_if                      #
    end_if                        #
    c=|S|                         # to prevent further tracing from the boundary
  end_if                          #
 
else                              # backtracking and left boundary

  if ( x==0 ) then                ## left boundary conditions ##
    o_L++                         # move to the next start point for tracing
    if (bounded) then             # for bounded lattices
      if ( b[o_L]>0 )             # check masking of the left overlap by the left boundary vector
        c=0                       # move to the next start point for tracing
      else                        # else if the current overlap is not valid
        o_L++                     # move to the next start point for tracing
      end_if                      #
    else_if (cyclic) then         # for cyclic lattices
      c=0                         #
    end_if                        #

  else                            ## backtracking ##
    o=(C[x-k0-1]*|S|^(k-1)+o)/|S| # backtracking to the previous overlap
    c=C[x+k-k0-1]                 # restoring the last used link at this overlap
    c++                           # at the backtracked overlap continue with the next link
    x--                           # decrementing the position index
  end_if                          #

end_if

end                               # if all start points are exhausted end the algorithm

算法复杂度

该算法可以分为两个耗时的操作

追踪和回溯
列出原像

该算法访问从起始边界开始可访问的所有链接和节点。重叠和邻域的可访问性定义为归纳法。

基础: 起始边界 $b_{L}$ （这里指左侧）处的重叠 $o$ 可访问，如果它们是有效的 $b_{L}(o)>0$ 。
归纳: 每个源自可访问节点的邻域都是可访问的。每个指向可访问且有效邻域的排放重叠都是可访问的。

有效的可访问链接恰好被访问两次（第一次在追踪时，第二次在回溯时），无效链接只被访问一次（它们的有效性在追踪时被评估）。追踪时间的简单近似值是计算所有可访问的重叠，必须对边界处的每个重叠进行计数，因此必须使用原像矩阵进行计数。

任意的重叠 $o_{x}$ 从左侧边界处的有效重叠 $o_{L}$ 可访问，如果两者的之间至少有一条有效路径 $p_{o_{L},o_{x}}>0$ 。位置索引为 $x$ 的重叠的可访问性可以从原像矩阵 $D_{L,x}$ 中提取，方法是将其元素转换为布尔值或使用布尔乘法来计算原像矩阵 $D^{B}$ 。追踪的算法复杂度是所有可访问重叠的总和。

T_{trace}=\sum _{x=0}^{l-1}b_{L}D_{L,x}^{B}b_{u}^{T}

处理时间的上限是观察到的配置大小 $l$ 的线性函数，但随着邻域大小（原像图大小）的增加而呈指数增长。

T_{trace}=O(l\cdot |S|^{2(k-1)})

列出原像所需的时间 $T_{list}$ 是原像数量 $p$ 的线性函数，其中计算单个原像的时间是配置长度 $l$ 的线性函数。

T_{list}=C_{list}lp=O(lp)\,

算法的内存消耗非常小，只存储了原像网络中的当前路径，并在找到有效原像时用于列出。

计数和列出算法

该算法包含一个第一阶段的反向或计数传递，用来计数原像，以及一个第二阶段的正向或列出传递，用来列出原像。跟踪和回溯算法必须追踪每条链接才能知道它是否会导致有效的原像，而另一方面，计数传递会生成关于每个链接是否存在原像以及原像数量的信息。所有原像都可以在不回溯的情况下列出。

列出传递的方向可以反转，但这里选择的方向是为了使列出的原像按照它们的紧凑表示升序排列，计数传递则相反。

正式算法描述

正向（从左到右，生成 $b_{L,x}$ 向量）和反向（从右到左，生成 $b_{x,R}$ 向量）的计数传递已经在上面描述，同时计算了原像网络的权重。只需要其中一个传递，这里使用的是反向传递。

列出传递可以分为初始化和主循环中的几个步骤。

初始化

由于原像的数量 $p$ 已经在计数传递中计算出来，因此可以提前为它们分配内存。起始重叠数组 $o_{L}$ 保存了每个原像（原像网络中的有效路径）的起始点的值。使用每个起始重叠的原像数量被计算为左侧边界重叠的权重向量。对于有界格，使用左侧边界和从右端到左端的原像计数。

w_{0}(o)=b_{L}(o)b_{0,R}(o)\,

对于循环格，使用整个序列的原像矩阵。

w_{0}(o)=D_{0,R}(o,o)\,

起始重叠数组被复制到当前位置索引 $o_{x}$ 处的重叠数组中，列出过程可以开始了。

列出

列出从左侧边界 $x=0$ 开始，到右侧边界 $x=l$ 结束。在位置索引的每次递增中，都会为 $p$ 个原像中的每一个计算一个单元格。

为了简化算法，邻域 $n_{x}$ 中的右侧单元格 $x+k-k_{0}-1$ 被存储。有界格上原像的第一个单元格 $-k_{0}\leq x\leq k-k_{0}-1$ 可以从起始重叠 $o_{0}$ 计算。对于循环格，右侧的最后一个单元格可以环绕到开头。

算法伪代码

C = malloc( p * (l+k-1) * |S| )            # reserve memory for the counted amount of preimages
                                           #
i = 0                                      # start with the first preimage
for ( o=0; o<|S|^(k-1); o++ )              # for all overlaps
  for ( j=0; j<b_L[0][o]*b_R[0][o]; i++ )  # for each overlap the number of preimages is calcuated
    o_x[i] = o                             # i-th preimage path begins with overlap o
    i++                                    # to the next preimage
  end_for                                  #
end_for                                    #
if (cyclyc)                                # for bounded lattices there is no need to know the starting points
  o_L = o_R = o_x                          # copy the current array of overlap to the array of starting overlaps
end_if                                     #

for ( x=0; x<l; x++ )                      # run from the left to the right
  i = 0                                    # start with the first preimage
  while ( i< p )                           # check if all preimages have been finished
    for ( c=0; c<|S|; c++)                 # check all links for each source overlap
      o_x[i] = (o_x[i]*|S|+c) / |S|^(k-1)  # calculate the drain overlap
      elseif (bounded)                     # for bounded lattices
        w = b_R[x+1][o_x[i]]               # the count from the drain node to the right end is used
      if (cyclic)                          # for cyclic lattices
        w = D_R[x+1][o_x[i],o_L[i]]        # the count from the drain node to the end node (same as left)
      end_if                               #
      for ( j=0; j<w; j++ )                # use the count
        C[i][x+k-k0-1] = c                 # and write a cell for each of them
        i++                                # increment the preimage counter
      end_for                              #
    end_for                                #
  end_while                                #
end_for                                    # end of algorithm

算法复杂度

计数的复杂度是配置长度 $l$ 的线性函数。对邻域大小 $k$ 的依赖关系不是立方的，因为单个单元的前像矩阵中最多有 $k$ 个非零元素。如果格是有界的，计数将存储为向量，复杂度为线性；对于循环格，计数将存储为向量，复杂度为二次。

T_{count,bounded}=C_{count}lk\,

T_{count,cyclic}=C_{count2}lk^{2}\,

列出的复杂度仍然是配置长度 $l$ 和前像数量的线性函数。

T_{list}=C_{list}l\cdot p

矩阵乘法计数处理前像图中的所有节点，而先前算法中的跟踪和回溯避免了一些节点，从而平均获得了更低的复杂度。另一方面，该算法更容易优化。

内存消耗是另一个缺点，它与计数的时间一样快地增长。

证明

参考文献

Andrew Wuensche 和 Mike Lesser，Cellular Automata 的全局动力学 一维 Cellular Automata 吸引盆域图集
Wuensche,A.，(1997)，离散网络的吸引盆域，萨塞克斯大学认知科学研究论文 461，D.Phil 论文
Vladimir Batagelj，用于引文网络分析的高效算法 (2003)
J. C. Seck Tuoh，G. Juárez 和 H. V. McIntosh，计算一维 Cellular Automata 中的祖先，现代物理学国际期刊 C，第 15 卷，第 8 号，第 1151-1169 页，2004 年 10 月
MathPages
- Cellular Automata
- Cellular Automata 的全局可逆性
Iztok Jeras，Andrej Dobnikar，计算 Cellular Automata 配置前像的算法 (PDF)

软件

DDLab 用于研究 Cellular Automata、随机布尔网络、多值离散动力系统等等的工具；由 Andy Wuensche 提供。
Iztok Jeras，计算 Cellular Automata 配置前像的算法 TAR.BZ2