电路想法/Deborah Chung 的“表观负阻”
电路想法:这种排列与负阻现象之间没有任何联系。
1998 年 7 月,Deborah Chung 和 Shoukai Wang 在 布法罗大学 展示了一项实验的结果,该实验显示了裸露的 碳纤维 在压力作用下表现出表观绝对负阻。[1]
在实验中,两束碳纤维以交叉形状排列,每束纤维的末端用铜箔和银漆短路(在图像中的 A、B、C 和 D 处)。电流驱动通过一个分支,电压测量通过另一个分支。在论文中,电压除以电流被称为“表观电阻”(真正的 电阻 要求电流和电压在同一位置进行测量。)
论文描述了当纤维被压缩时,界面表观接触电阻如何从正值变为负值。然后,所测量的“负阻”的电流-电压特性是通过原点的负斜率的直线。表观负阻也出现在金属导线(银包铜)中,但没有观察到单根纤维与另一根单根纤维交叉的情况。论文声称这种现象很有用,因为同一材料中电子的正向流动和反向流动可以通过外力可重复地控制。
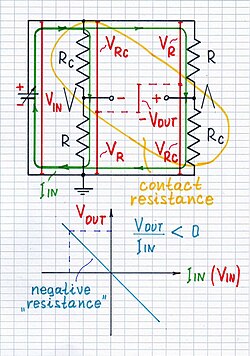
如果我们仔细研究这种奇特的碳纤维排列,我们会意识到它起着某种桥式电路的作用,该电路由两种电阻组成——稳定的碳纤维电阻 R 和变化的接触电阻 Rc。以某种方式(目前无法识别),它们被连接到相反的桥臂上。顺便说一句,很久以前,我对桥式电路的这个非凡特性印象深刻——反转输出电压。它可以做到这一点,因为输出电压是一个差值。它在“飞行”;它是两个接地电压之间的差值——VR 和 VRc。根据 R 和 Rc 之间的比例,这个差值可以为零 (R = Rc)、正 (R > Rc) 或负 (R < Rc)。并且,如果我们假设电流 IIN 是输入量,电压 VOUT 是输出量,我们可以将该设备视为零、正或...“负”跨阻抗转换器:) 但这不是负阻;它甚至不是阻抗;它是更加抽象的跨阻抗。
 |
 |

|


好吧,让我们看一下图 2 并开始思考...... 两个薄片通过大量接触电阻 Rc 连接在一起;你可以将中心交叉区域视为一种立方体。电流从正极的顶部薄片流向负极的底部薄片。因此,上面的点 B 是正的,下面的点 D 是负的;输出电压 VOUT 具有与图中所示相同的极性。 “电阻”为正:R = VOUT/IIN > 0。


现在,让我们看一下图 3 并继续一起思考。现在,施加了很大的压力;因此,两个薄片通过大量零接触电阻连接在一起。在这种情况下,中心交叉区域是一个平坦的网格。电流从网格的左侧流入,转向底部,然后从网格的底部流出。在这种情况下,点 D 离输入电压源的正极更近,点 B 离负极更近。因此,点 D 比点 D 更正,输出电压 VOUT 具有右侧图中所示的负极性。因此,就像 Chung 教授一样,我们可能会得出错误的结论,即“电阻”是“负的”:R = -VOUT/IIN < 0 并开始制造轰动。
最后,我们可以假设在输出电压 VOUT 为零的极端限制之间存在一些中等压力。 “电阻”也为零:R = VOUT/IIN = 0。
那么,Deborah Chung 教授实际上观察到了什么?她做了什么?让我们尝试回答......
很明显,她制作了一种依赖于施加压力的奇特桥式电路。实际上,这种碳纤维结构可以充当一个奇特的电压到电压转换器、电流到电压转换器,或者充当一个(较差的)压力到电压转换器(压力传感器)。但在我看来,使用它没有任何好处;相反,它有许多损失……只要在Google上看看有多少人参与了这个毫无意义的讨论,以及浪费了多少精力、时间和金钱……看到人们更多地依赖“信誉”来源而不是他们自己的常识而被误导,真是令人惋惜!
这个实验与负阻现象没有任何联系。
这种结构中没有任何明显的、绝对的、微分的或动态的电阻;只有普通的、裸露的“19世纪”欧姆电阻。
Chung 的碳纤维网络实际上表现为一个奇特的桥式电路,取决于施加的压力(就像普通的应变式桥式电路一样)。
似乎 Chung 的实验是负阻现象领域的最大误解。
参考资料
[edit | edit source]- ↑ 碳纤维复合材料中的表观负电阻 — 王守凯,D.D.L. Chung — 复合材料研究实验室,纽约州立大学布法罗分校 — 1998 年 4 月 8 日收到;1999 年 3 月 31 日接受
