电路构思/如何产生正弦振荡?
电路构思:将两个异构能量存储元件连接在一起,并给其中一个元件充电。

LC 谐振回路是一个传奇的电路,在 LC 谐振回路中产生正弦振荡是一种常见的电气现象。它在物理、电气和电子资源中得到了很好的描述(例如,参见网络上关于 LC 谐振回路的最佳解释之一[1])。浏览这些资源,您可能会了解什么是 LC 谐振回路以及它在电气方面的运作方式。只是,尽管这些资源详细解释了 LC 谐振回路的作用,但它们没有说明它如何以及为什么能够实现这种神奇的效果。
关键是 LC 振荡不仅仅是一个特定的电气现象;它是一个伟大的世界现象。它在“非电气”世界(力学、气压学、液压学等)中有着许多表现形式。如果您想深入了解其本质,您将开始提出许多仍然没有答案的“哲学”问题。这些问题是什么?以下列出了一些问题。
为什么 LC 谐振回路由两个“异构”积累元件(电容和电感)组成?为什么它不由两个“同构”元件(两个电容或两个电感)组成?这些元件在 LC 回路中的作用是什么?它们实际上在那里做什么?它们是什么?为什么 LC 谐振回路中的能量“永不平静”?是什么导致能量在两个元件之间循环(理论上无限循环)?是什么导致积累元件完全放电?为什么 LC 振荡具有正弦波形?为什么它不是线性的或其他形状?为什么 LC 固有频率不依赖于“推动”能量的大小?为什么振荡曲线是对称的?LC 振荡与其他(RC、弛豫等)振荡有什么区别?它们之间有什么相似之处,是什么?双元件 LC 谐振回路与单元件摆之间有什么联系?摆中的“电容”和“电感”是什么?
在这个故事中,我们将以一种与传统方式截然不同的方式回答这些问题。在这里,我们将暂时忘记传统的“电气” LC 解释(例如,“...电感通过电容放电,场崩溃...”);它们并不能帮助我们很好地回答上述问题。因为我们人类不能用具体(电气)解释来理解具体(电气)现象。为了理解具体的电气概念,我们需要首先揭示具体电气现象背后的最一般、非电气概念。
在这个激动人心的故事中,我们,电路构思者和电路哲学家,将尝试自己找出关于这个伟大世界现象的真相。为此,我们将重新发明并逐步构建著名的 LC 谐振回路,以便掌握其背后的基本思想。因此,我们将为特定的电气 LC 现象创建一个通用的、非电气哲学。
通用源。首先,要在世界上做点什么,我们需要一个稳定的电源。根据两种能量 - 动能和势能,也有两种电源 - 流状电源和压力状电源(见图 1a 顶部)。流状电源保持恒定的流量,而压力状电源保持某种物质(空气、水、油、弹簧张力等)的恒定压差 - 图 1b。

电气源。类似地,在电气中,我们也有两种电源 - 电流源保持恒定电流,而电压源保持恒定电压(见图 1a 底部)。
问题。只是,由于各种原因,我们希望稳定电源的输出量随着时间的推移开始周期性变化。当然,我们可以取一个可变电源并开始控制它;但是,我们希望它自发振荡,无需我们的帮助。因此,问题是
首先,我们必须使稳定量依赖于(随着)时间而变化。此时,它如何随时间变化并不重要;重要的是它随时间变化。因此,主要问题是:我们如何产生随时间变化的数量?
哲学。显然,我们必须在时间内开始某个过程(但时间是什么?:)为了使某物发生变化,我们必须从它那里获取或赋予它;这意味着要将某物从一个地方移动到另一个地方...一个电源不足以实现此目的,因为它保持其输出量的稳定性;我们需要两个元件 - 源和负载相互连接,以开始将能量从源传输到负载(以及可能相反)。我们已经有一个电源;剩下的就是选择负载类型。
积累的需求。电阻在这种情况下是无用的,因为它可以瞬时改变电流(当电压瞬时改变时)。电阻不能存储能量,它不能“记忆”。很明显,我们必须开始将一些量传输并存储在一个积累元件(一个积分器)中。积分器可以积累能量、物质或信息;它们主要存储能量。因此,我们可以通过持续向积累器添加能量来使其输出量增加,并通过持续从积累器中减去能量来使其输出量减少。根据两种能量 - 动能和势能,我们可以构建两种类型的积分器 - 流到压力和压力到流积分器。
流压积分器。 在这种情况下,我们开始将一个类流量(携带动能)转换为一个类压力(携带势能),并将其存储到一个具有包含属性的累积元件中(参见图 2a 的顶部)。能量从流动转移到压力累积器,类压力量随着时间的推移线性变化(图 2b)。

示例: 移动的质量推一个弹簧,一个加速的摆锤升起,一个孩子上紧发条电机,一个弓箭手拉弓,一个飞轮使玩具汽车运动,一个电机举起一个质量,一个气泵充气轮胎,一个水泵填充水库等等。我们甚至可以为了感受这个过程,想象我们自己在移动(在联想思维中,这种创造性思维技巧被称为“移情”)。
请注意,流压积分器由两个相互连接的异质元件组成 - 动能源和势能累积器。如果我们将两个同质元件相互连接(一个动能源和一个动能累积器),就会出现一个很大的压力,并且过程会暂时停止;这种安排将进行微分而不是积分。一个机械示例:想象一下,如果一辆移动的汽车撞上一辆静止的汽车会发生什么。
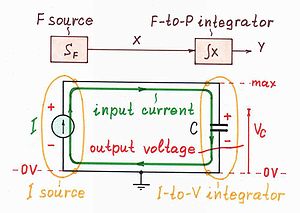
电流-电压积分器。 在电学中,我们有两种可以累积能量的元件 - 电容器存储势能,电感器存储动能。因此,我们可以构建两种类型的电积分器 - 电流-电压积分器和电压-电流积分器。让我们从第一个也是最流行的开始。
根据一般流压布置,在电流-电压积分器中,我们开始将电流(携带动能)转换为电压(携带势能),并将其存储到电容器中。因此,该电路包括一个为电容器充电的电流源(参见图 2a 的底部)。结果,电容器两端的电压随时间线性变化(图 2b)。请注意,电流进入电容器的正极板;因此,电容器在这里充当负载。
该电路由两个相互连接的异质电元件组成 - 电流源和电容器。如果我们将两个同质元件相互连接(一个电流源和一个电感器),它们之间会出现高电压,并且过程会暂时停止;该电路将进行微分而不是积分。
圆弧...
[edit | edit source]到目前为止,我们已经使稳定量随时间线性变化。因此,我们获得了随时间不断增加的量。在许多情况下(例如,在斜坡发生器中),这是一个理想的特性;但在这里,我们需要正弦形状,而不是线性形状。所以,新的问题是,“我们如何将线性曲线圆化?”
然后,让我们仔细检查当前的线性曲线,试图找到将其转换为正弦形状的补救措施。这意味着什么?这意味着在量线性变化一段时间后,此时它已经开始改变(减小)其斜率,弯曲,"失去勇气"(图 3b)。我们如何实现这样的效果?
总体思路。 到目前为止,我们已经通过一个对恒定量进行积分的积分器获得了线性变化。现在,我们问自己,“我们如何使积分器减缓其输出量的变化?”答案是:“通过减小输入量。” 这是所需的基本思想 - 减小输入量。
...通过降低有效电压...
[edit | edit source]记住不完美的 RC 积分器,其线性曲线自然圆化(呈指数形状)。


这个积分电路(图 3a)的“问题”(在这里,这是一个优点)是电容器正在被一个不完美的“自制”电流源(由电压源 V 和电阻 R 组成)充电。结果,负载(电容器)上的电压降 VC 使激励电压 V 虚弱;通过这种方式,它会干扰不完美的电流源。在这种情况下,电压差 VR = V - VC 决定电流 I 而不是激励电压 V。随着创建电流的电压 VR 随时间减小,电流也减小。由于这种随时间减小的电流源,VC 的曲线也开始减小其斜率;这就是我们在这里想要的。
...通过减小输入电流...
[edit | edit source]但这里我们有一个完美的电流源,其电流不依赖于负载(电容器)上的电压。这意味着,如果负载电压升高,我们的电流源也会增加其内部激励电压,从而消除电压干扰。[2] 这看起来很奇怪,但这里的问题恰恰是完美的电流源:) 那么我们该怎么办?我们如何使其表现得不完美?
看着图 3,我们脑海中可能会开始形成一些新想法的萌芽... 事实证明,我们可以通过某种方式使完美的电流源开始自动减小负载电压升高时产生的电流,从而设法圆化、改变并最终减小曲线的斜率... 我们可以概括这个断言
而在不完美的 RC 积分器中,圆化是降低有效创建电流的电压 VR 的结果,而在这里,圆化将是降低整个输入电压 V 的结果。好吧,这很棒,但我们如何实现这种魔法?
当然,我们可以调节输入电压,但这将需要一些电子电路。请不要忘记,在这里我们“发明”了可以振荡的最简单的“东西”;因此,我们需要最简单的“技巧”!是什么?
...通过耗尽输入电流源
[edit | edit source]看起来另一个新的想法开始形成... 我们想减少一个量... 它是由电源产生的... 它有一个有限的能量储备... 哈哈!如果我们开始从电源中取走能量,它的输出量就会开始减小!这里有一些例子:推弹簧,移动的质量开始减速;撞到弹性障碍物,我们会减慢你的跑步速度;上升,摆锤开始减速,等等。


正确的想法。 如果以某种方式,输入电流源开始减弱、消耗、耗尽其能量储备,电流源的电流也会开始减小(图 4a)。结果,电容器两端的电压将开始缓慢变化,并且其曲线将开始“失去勇气”(图 4b)。这个源是不是像上面那样一个不完美的电流源?不,它不是;它是一个正在耗尽但仍然是完美的恒定电流源,它逐渐降低其输出量。在这里,电流的减小不是因为负载电压(就像不完美的 RC 积分器那样),而是因为负载消耗!
什么电气元件可以充当这样的耗尽的完美电流源?当然,一个充满动能的电感器!这看起来很奇怪,但它会产生一个“恒定”的电流(对于快速负载变化),并且该电流会逐渐减小
哈哈!我们已经获得了所需的布置(图 4a);我们几乎“发明”了 LC 振荡电路
请注意,电流离开电感器的正极引线;因此,电感器在这里充当源。
停止“运动”
[edit | edit source]我们已经到达了曲线的顶端,现在是时候在这里停下来了。但是我们如何使积分器的输出量停止?如果我们停止输入量,它会停止吗?不会。即使我们将输入量显着降低,积分器也不会停止改变其输出量。停止积分器输出量的唯一方法是将输入量归零。为了说服你自己相信这种现象,想象你用一个容器装满了水:即使你将流量降低到一个微不足道的量,水位仍然会继续上升。更多例子:如果你用零钱逐渐补足一个存款,那么金额会随着时间的推移而缓慢增加(但仍然增加);推弹簧,移动的质量最终会停止;移动的摆锤在顶部停止。


上面提到的“耗尽”流源 above,它产生逐渐减小的流量,已经帮助我们改变了曲线的斜率并使其变得圆滑。现在,在曲线的顶端,它可以帮助我们停止“运动”。实际上,在数量达到最大值时,该源已完全耗尽其动能储备。实际上,在这个时刻,它不仅仅是一个源;它是一个空源。因此,流量变为零(图 5a),积分器停止改变其输出量(图 5b)。然后,让我们得出另一个结论
在电气实现(LC 谐振回路)中,电感器充当耗尽电流源(图 5a)。在曲线的顶端,它已完全放电,不再产生电流。因此,电容器两端的电压停止变化。
为什么电感器完全放电?我们已经 said 电感器是一个耗尽的,但仍然是完美的恒流源。此外,电感器是一个自然的、纯净的、整体的电流源;它不是一个人工的电流源,它不像 imperfect RC integrator 中那样由内部电压源和电阻组成。这意味着它可以在负载上产生足够高的电压来产生所需的电流。换句话说,电感器产生的电流不依赖于电容器两端的电压;该电压不是电流的“阻力”。由于没有任何东西阻碍电感器产生的电流,无论电感器中剩余多少能量,电流都会持续流动,直到电感器完全放电。
相反的安排。为了感受这种差异,将这种“放电电感器 -> 充电电容器”的安排与 下面 提到的“放电电容器 -> 充电电感器”的安排进行比较。在后一种情况下,带电的电容器正在放电,空的电感器正在充电。这样,这两个元件最终都带有一些能量。它们两端的电压具有某个中间值 - 系统平衡点。
到目前为止,我们一直在一个方向上“移动”(最初快,然后慢),最后我们在曲线的顶端停了下来。由于我们一直在不断地将能量“推入”累加器(积分器),因此其输出量一直在不断地增加。因此,我们得到一个单调且相当无趣的信号:) 然而,我们希望得到一个周期性的量;所以,我们在这里,在曲线的顶端,以某种方式改变“运动”的方向。在这点上必须发生某些事情才能使积分器的输出量开始减少... 什么会导致这种情况发生?
查看许多积分的类比,我们可以得出结论,改变积分器(这里是一个类似压力的)输出量方向的唯一方法是改变其输入(这里是一个类似流动的)量的方向,而不是其大小。再次想象水流的类比:当我们给容器注水时,水位会上升;为了让它下降,我们必须开始清空容器。或者想象一下金钱的类比:当你逐渐增加存款时,随着时间的推移,金额会增加;为了让它减少,你开始“清空”存款。当然,我们应该再次提到著名的机械类比:移动的质量停止后,弹簧开始将它击回;在我们撞击弹性屏障后,它会反弹我们,它就像一种“反转器”,改变了我们的运动方向。我们已经准备好得出两个结论
但是这个积分器不仅仅是一个简单的累加器... Remember 到目前为止,一个类似流动的源一直在缓慢地耗尽并为这个压力累加器(一个流到压力的积分器)充电。因此,在这个过程结束时,积分器已经转变为相反的压力源。现在,它是一个充满能量的累加器;它已经成为一个电源!因此,它可以自行通过负载传递电流来改变其输出量。但这里的负载是什么?另一个元件(前源)现在充当负载。它是什么类型的负载? Remember 它是一个存储动能的累加元件。
压到流的积分器。因此,我们现在开始将一个类似压力的量(携带势能)转换为一个类似流动的量(携带动能),并将其存储在一个具有惯性特性的累加元件中(见图 6a 的顶部)。现在,能量以相反的方向移动 - 从压力累加器到流量累加器,并且类似流动的量应该随着时间的推移线性变化(图 6b)。


示例:弹簧(或重力)使质量运动,弹簧马达驱动玩具,孩子加速飞轮汽车,储存在储气罐中的压缩空气旋转空气涡轮机,储存在湖泊中的水旋转水轮机,巨石从山上滚下来,速度越来越快,“踩油门”使恒功率发动机推动汽车加速,从气球火箭中逸出的加压空气使其加速飞行,水火箭,“用脚推”使自行车开始运动,等等。
请注意,这种安排再次包括两个连接在一起的异类元件 - 一个势能源和一个动能累加器。如果我们将两个同类元件连接在一起(现在,一个势能源和一个势能累加器),就会产生一个大电流,并且该过程会立即停止。正如 above,这种安排将进行微分而不是积分。
电压到电流的积分器。根据一般的压到流安排,在电压到电流的积分器中,我们开始将电压(携带势能)转换为电流(携带动能),并将其存储在电感器中。因此,该电路包括一个为电感器充电的电压源(见图 6a 的底部)。因此,电感器中的电流应该随时间线性变化(图 6b)。请注意,电流离开电容器的正极板(因此,它在这里充当源),电流进入电感器的正极板(因此,它在这里充当负载)。
该电路由两个连接在一起的异类元件组成 - 电压源和电感器。如果我们将两个同类元件连接在一起(一个电压源和一个电容器),就会有一个大电流流过它们,并且该过程会立即停止;该电路将进行微分而不是积分。
耗尽的电压源 如 above,为了使曲线变圆滑,我们的源必须具有有限的能量储备;它必须逐渐耗尽,逐渐减少。电容器恰好充当这种耗尽的电压源。只是,我们 before 希望在最后部分使曲线变圆滑,而这里我们希望在初始部分使曲线变圆滑。让我们看看情况如何。在开始时,电流很小,电感器消耗的能量很少。后来,流经电感器的电流增加,它开始从电压“源”中消耗越来越多的能量。太棒了!曲线在其初始部分变圆滑,正如我们所期望的那样!
在这个阶段结束时,该源已完全耗尽其势能储备。如上所述,在这个时刻,它不是一个源;它只是一个空的源。因此,压力变为零(见图 7a 的顶部),压到流的积分器停止增加其输出量(图 7b)。它在这个时候积累了最大的动能。
如果你再次查看我们最喜欢的类比,你会发现上面所有机械示例中的移动质量都被最大限度地加速(例如,想象一下我们在这个时候跑得有多快:) 这里,我们必须记住,这些物体有一个有趣的特性 - 惯性。如果它们没有惯性,它们就会在这个时候停止,并且系统将处于平衡状态。但它们有惯性;这就是为什么,它们会越过这个零点(中性位置)并继续运动... 就好像有一些恶魔般的力:) 使它们继续越过这个点(记住牛顿运动定律)。


我们已经可以比较两种不同累加元件的行为。我们 already 已经看到了势能累加器(电容器)如何充当一种弹性屏障,它会反弹移动的“质量”,从而反转运动的方向。现在,我们可以看到动能累加器(电感器)由于其固有的惯性,“越过”平衡点(零电平)并继续“移动”。
不久前,电容器充当着耗尽的电压源。此时,它已经完全放电,并且在其两端没有电压。电感器中的电流达到最大速率,但它已经停止变化。因此,在这个阶段结束时,电流和能量消耗都增加到最大值。
相反的安排。我们已经成功地回答了为什么 电感器 会通过电容器完全放电 - 因为它是一个自然的真正电流源。现在情况更加有趣。为了回答为什么电容器会完全放电,让我们再次考虑 相反的安排 - 一个带电的电容器连接到一个空的电容器。如果你喜欢类比,想象一下两个连通的容器,其中一个容器是满的,另一个是空的。我们知道结果:一开始会有很大的电流;最初空电容器两端的“相反”电压(最初空容器的水位)开始迅速上升;结果,它下降并最终停止电流。此时,能量分布在两个电容器之间,系统处于静态平衡(记住牛顿第三定律)。最初带电的电容器并没有完全放电。
为什么电容器会完全放电?相反,如果我们将带电的电容器连接到一个最初空的电感器(本例中的情况),电流在一开始是微不足道的,电容器开始缓慢地通过电感器放电。随着时间的推移,电感器允许电流逐渐增加。增加的电流越来越多地放电电容器,从而加快其放电速度;最后,电容器完全放电。形象地说,电感器具有时间相关的行为:在一开始,它消耗的电流很少,但最终它会吞噬大量的电流(电容器具有相反的时间相关的行为 - 一开始,它会吞噬最大的电流,但最终它消耗的电流很少)。
乍一看,似乎系统正在向平衡状态移动;我们可能会假设它已经成功地到达了这一点,并且居住在 LC 振荡回路中的能量“已经找到了安宁”...
创建正弦曲线的后半部分
[edit | edit source]到目前为止,我们一直在详细地考虑如何创建正弦曲线的前半部分(第一和第二象限)。常识表明,我们可以用相同的方式创建后半部分。那么,让我们试一试。
第三象限
[edit | edit source]

在第二象限结束和第三象限开始时,情况与第一象限相同。一方面,电感器充满动能,并且再次从积分器转变为电流源(图 8a)。另一方面,空电容器连接到此“电流源”。那么电感器会开始做什么呢?当然,它将开始给电容器充电并开始逐渐放电。唯一的区别是电流的方向,它在电容器两端产生负电压。结果,曲线开始下降(一开始是迅速下降,然后是缓慢下降)并最终在底部停止。正如我们所期望的,它在最后的部分是圆形的。
第四象限
[edit | edit source]

类似地,在最后第四象限的开始,情况与第二象限相同。一方面,电容器充满势能,并且再次从积分器转变为电压源(图 9a)。另一方面,空电感器连接到此“电压源”。那么电容器会开始做什么呢?当然,它将开始给电感器充电并开始逐渐放电。唯一的区别是电容器两端的负电压,它会产生具有相反方向的电流。结果,曲线保持在零点以下,但开始上升(一开始是缓慢上升,然后是迅速上升)并最终穿过零点(图 9b)。正如我们所期望的,它在最初的部分是圆形的。
概括
[edit | edit source]在这个不可思议的故事的结尾,让我们概括一下我们所做的事情。
基本结构
[edit | edit source]
在一开始,我们组装了一个系统,该系统由两个相互连接的异质元素组成,这些元素可以处理两种不同的能量:它们可以转换能量(充当真正的能量转换器)、储存能量(充当累加器)和供应负载能量(充当源)。其中一个可以将势能转换为动能、储存动能并将此动能逐渐转移到负载,从而保持逐渐减小的流动量;另一个元素可以将动能转换为势能、储存此势能并将此势能逐渐转移到负载,从而保持逐渐减小的压力量。第一个元素具有惯性的属性,而第二个元素具有应变的属性;因此,第一个元素可以“越过”平衡点并继续运动,而第二个元素可以反转“运动”的方向。这些可逆元素中的每一个都可以充当负载,也可以充当逐渐耗尽的源。这些类型的可充电源彼此完美地匹配 - 当一个元素充当流量输出源时,另一个元素充当流量输入负载,反之亦然 - 当另一个元素充当压力输出源时,第一个元素充当压力输入负载。结果,它们可以随着时间的推移逐渐地彼此交换能量。
电路
[edit | edit source]在电气中,我们通过将电感器和电容器连接在一起实现了这种安排;因此,我们获得了著名的LC 振荡回路。电感器可以将电压转换为电流,将移动电子在磁场中的动能储存起来,并将此动能逐渐转移到负载,从而保持逐渐减小的电流;电容器可以将电流转换为电压,将此势能储存到静电场中,并将此势能逐渐转移到负载,从而保持逐渐减小的电压。简单地说,电感器充当可充电电流源,而电容器充当可充电电压源。
操作
[edit | edit source]在一开始(参见图 11 中的点a),LC 振荡回路中没有能量;它处于静止状态。然后,我们通过短暂地连接一个电流源来给电感器充电(我们也可以通过短暂地连接一个电压源来给电容器充电,而这在电子振荡器中是更常见的情况)。在我们断开电源后,奇迹开始了...

阶段 1。电感器(充当正电流源)通过电容器(充当累加负载)逐渐放电。能量从左向右移动;电压上升到零点以上。在顶部(点b),电容器成为一个正电压源。
阶段 2。电容器(充当正电压源)通过电感器(充当累加负载)逐渐放电。能量从右向左移动;电压下降到零点以下。最后(点c),电感器成为一个负电流源。
阶段 3。电感器(充当负电流源)通过电容器(充当累加负载)逐渐放电。能量从左向右移动;电压下降到零点以下。在底部(点d),电容器成为一个负电压源。
阶段 4。电容器(充当负电压源)通过电感器(充当累加负载)逐渐放电。能量从右向左移动;电压上升到零点以上。最后(点e),电感器成为一个正电流源。
组装。如果电路中没有损耗,四个阶段将连续地一个接一个地重复(1 - 2 - 3 - 4 - 1 - 等),从而形成完整的 LC 正弦振荡(图 11)。LC 振荡回路保持最初注入的能量完整,但这种能量并不处于静止状态,它“没有安宁”。居住在 LC 振荡回路中的能量在两个元件之间连续地来回移动,并交替地从一种形式变为另一种形式。因此,代表相应能量类型(动能和势能)的电量(电流和电压)以正弦方式变化;因此,我们可以将它们用作输出。
能量独立性。正如我们所见,在我们将能量注入 LC 谐振电路后,它就开始产生一个具有自然周期的正弦振荡。如果我们注入更多的能量,电压和电流的振幅会增加,但它们的变化也会更快,反之亦然;因此,自然周期保持不变。这种“能量无关的时间行为”的原因是可变消耗:当我们增加最初注入的能量时,消耗也会增加,反之亦然。在用更多能量为电感器充电的情况下,通过电感器的电流将达到更大的幅度,然后,当我们断开“推动”电流源时,这个更大的电流将决定更大的消耗;因此,时间保持不变。在另一种情况下,当我们用更多能量为电容器充电,然后断开“推动”电压源时,电感器将开始逐渐消耗更大的电流;因此,时间再次保持不变(我们可以在RC 电路中观察到类似的“时间常数”效应)。因此,我们可以得出结论:LC 振荡的自然频率不依赖于“推动”能量的多少(电压和电流的幅度)。
LC 依赖性。相反,如果我们改变蓄能元件(电感器和电容器)的“存储属性”(电感 L 和电容 C)的值,自然频率也会改变。我们可以很容易地从直觉上认识到,存储属性的值越大,相应四分之一周期的持续时间就越长(例如,如果电容器“更大”,电感器需要更多时间来为其充电)。
对称性。但是为什么振荡仍然是对称的(TPhase1 = TPhase2 = TPhase3 = TPhase4),即使我们只改变一个存储属性(电感 L 或电容 C)的值?答案很简单。在每个半周期内,两个元件中的每一个都会两次改变其“角色”:在第一个四分之一周期内它充当负载,在第二个四分之一周期内它充当电源。这样,它的存储属性决定了相邻两个四分之一周期的持续时间;改变该属性,我们同时改变两个四分之一周期的持续时间。因此,当我们改变电感 L 或电容 C 或两者时,曲线保持对称。
LC 谐振电路是最简单的可以产生具有完美正弦形状振荡的电路。这种独特的电路仅由两个元件组成,但它可以自行完成产生正弦振荡所需的一切。它是一个几乎理想的电路,类似于永动机:) - 我们只需要注入初始能量,然后它就可以自行持续运行。
振荡 是维基百科关于自然界振荡的一篇通用文章。
- ↑ 一个电摆 by Tony Kuphaldt 是一个经典但可能是关于 LC 谐振电路操作的最好书面故事,尽管它似乎暗示摆表现出简谐运动(它们不是,完全)。
- ↑ 通过跟随激励电压保持恒定电流揭示了恒定电流源的原理。
- 振荡器简介 和
- LC 振荡器 很好地展示了 LC 谐振电路操作的经典“电气”观点。
- 并联 LC 电路如何存储能量 是另一个优秀的 LC 资源。
- 关于 LC 电路的讲座 是一系列包含有用公式的幻灯片。
- LC 谐振电路 是一个关于 LC 谐振电路的有趣且图文并茂的故事。
- 共振的物理学 是一个经典但写得很好的关于 LC 谐振电路操作的故事。
- 特斯拉线圈的工作原理 对 LC 谐振电路有一个简明但信息丰富的介绍。
- LC 电路 对电气和机械实现进行了比较。
- 电感器 - 关于电感器行为的优秀材料。
