通信系统/调幅

调幅是最早的无线电调制技术之一。用于收听 AM-DSB-C 的接收机可能是所有无线电调制技术中最简单的接收机；这可能是为什么该版本的调幅至今仍被广泛使用。在本模块结束时，您将了解最流行的调幅版本、一些流行的 AM 调制电路和一些流行的 AM 解调电路。

调幅

调幅 (AM) 发生在载波的振幅被调制时，以对应于源信号。在 AM 中，我们有一个这样的方程式

$A_{signal}(t)=A(t)\sin(\omega t)$

我们还可以看到，此波的相位无关紧要，并且不改变（因此我们甚至没有将其包含在方程式中）。

调幅双边带（简称 AM-DSB）可分为两种不同的类型：载波和抑制载波变体（分别简称 AM-DSB-C 和 AM-DSB-SC）。本页将讨论这两种变体，并讨论每种变体的异同。

特性

调制指数

调幅需要一个高频恒定载波和一个低频调制信号。

载波的形式为 $e_{c}=E_{c}\cos \left({\omega _{c}t}\right)$

调制信号的形式为 $e_{m}=E_{m}\cos \left({\omega _{m}t}\right)$

请注意，高频载波的振幅呈现出低频调制信号的形状，形成了所谓的调制包络。

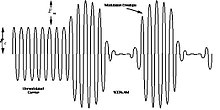
调制指数定义为调制信号振幅与载波振幅之比。

$m_{am}={\frac {E_{m}}{E_{c}}}$ 其中 $0\leq m_{am}\leq 1$

总信号可以用以下公式描述

$e_{am}=\left({E_{c}+E_{m}\cos \left({\omega _{m}t}\right)}\right)\cos \left({\omega _{c}t}\right)$

更常见的是，载波振幅被归一化为 1，am 方程式写成

$e_{am}=\left({1+m_{am}\cos \left({\omega _{m}t}\right)}\right)\cos \left({\omega _{c}t}\right)$

在大多数经验丰富的作者的书籍中，这个表达式简写为

$e=\left({1+m\cos \omega _{m}t}\right)\cos \omega _{c}t$

如果调制指数为零 ($m_{am}=0$)，信号就只是一个恒定幅度的载波。

如果调制指数为 1 ($m_{am}=1$)，则所得波形具有最大或 100% 的幅度调制。

边带

展开归一化 AM 方程

$e=\left({1+m\sin \omega _{m}t}\right)\sin \omega _{c}t$

我们得到

$e=\sin \omega _{c}t+{\frac {m}{2}}\cos \left({\omega _{c}-\omega _{m}}\right)t-{\frac {m}{2}}\cos \left({\omega _{c}+\omega _{m}}\right)t$

其中

$\sin \omega _{c}t$ 代表载波

${\frac {m}{2}}\cos \left({\omega _{c}-\omega _{m}}\right)t$ 代表下边带

${\frac {m}{2}}\cos \left({\omega _{c}+\omega _{m}}\right)t$ 代表上边带

边带占据中心频率两侧。它们是载波和调制信号的和频和差频。在上面的例子中，它们只是单个频率，但通常基带调制信号是一系列频率，因此形成两个频带。

AM 调制器

标准幅度调制方程为

$e_{am}=\left({1+m\sin \omega _{m}t}\right)\sin \omega _{c}t$

由此我们注意到 AM 涉及一个乘法过程。有几种方法可以通过电子方式执行此功能。最简单的方法是使用开关。

开关调制器

开关调制器可分为两类：单极性和双极性。

双极性开关调制器

双极开关最容易可视化。请注意，AM 波形似乎由一个低频直流信号组成，该信号的极性以载波速率反转。

AM 信号可以通过将直流调制信号乘以

这看起来很复杂，但是如果方波开关函数的占空比为 50%，则简化为

$F\left\{{f\left(t\right)}\right\}={\frac {4}{\pi }}\sum \limits _{n=1,3,5...}^{\infty }{\frac {1}{n}}\cos \left({\frac {n2\pi t}{T}}\right)$

这告诉我们，方波实际上是由一系列余弦波（相移正弦波）组成的，这些余弦波是基本开关频率的奇数倍。因此，使用此信号乘以基带信号会导致在开关（载波）频率的每个奇次谐波上生成 AM 信号。由于谐波的幅度迅速下降，因此此技术仅对前几个谐波是实用的，并且会产生大量不需要的信号（噪声）。

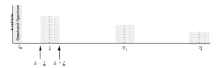
可以使用带通滤波器来选择任何一个 AM 信号。如果乘法器接受载波输入的正弦波，则可以显着减少不同输出频率的数量。

从输入中去除直流分量可以消除载波信号并产生 DSBSC 调制。

从物理上讲，这是通过反转信号引线来完成的

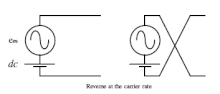
反转信号极性的过程可以通过在差分放大器的输出端放置两对开关轻松实现。 Mc1496 平衡调制器 是这种器件的一个例子。

单极开关调制器

如前所述，可以通过将直流调制信号乘以 0 和 1 来创建 AM 信号。

此信号的频谱由

$F\left\{{f\left(t\right)}\right\}={\frac {1}{2}}+\sum \limits _{n=1}^{\infty }{{\frac {2}{n\pi }}\sin \left({\frac {n\pi }{2}}\right)}\cos \left({\frac {n2\pi t}{T}}\right)$

从物理上讲，这是通过以载波速率打开和关闭调制信号来完成的

可以使用高幅度载波来打开和关闭二极管。在调制信号上施加直流偏压，以确保只有载波（而不是调制信号）可以反向偏置二极管。

这可能并不明显，但此电路的输出包含一系列 AM 信号。需要带通滤波器来提取所需的信号。通常是基波的第 1 次或第 3 次谐波。（第 1 次谐波是基波。）

集电极调制器

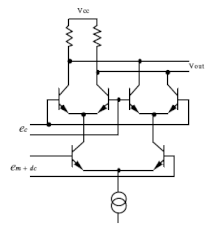
二极管开关调制器由于是无源器件，因此无法产生高功率信号。可以使用晶体管来克服此限制。集电极调制器用于高电平调制。

平方律调制器

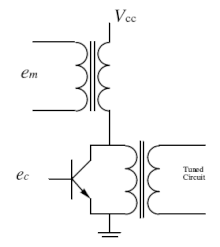
二极管的电压电流关系在拐点附近是非线性的，形式为

$i\left(t\right)=av\left(t\right)+bv^{2}\left(t\right)$

系数 a 和 b 是与特定二极管相关的常数。

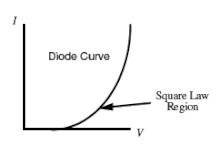
如果信号组合时二极管保持在平方律区域，则会发生幅度调制。

设注入的信号形式为

$k={\rm {dc}}\;{\rm {bias}}$

$e_{m}=E_{m}\sin \omega _{m}t={\rm {modulation}}\;{\rm {signal}}$

$e_{c}=E_{c}\sin \omega _{c}t={\rm {carrier}}\;{\rm {signal}}$

施加在二极管和电阻器上的电压由下式给出

$v\left(t\right)=k+e_{m}+e_{c}$

二极管中的电流，因此电阻器中的电流由下式给出

$i\left(t\right)=a\left({k+e_{m}+e_{c}}\right)+b\left({k+e_{m}+e_{c}}\right)^{2}$

展开后为

$i\left(t\right)=\underbrace {k\left({a+bk}\right)} _{\rm {dc}}+\underbrace {\left({a+2bk}\right)e_{m}} _{{\rm {original}}\;{\rm {modulating}}\;{\rm {signal}}}+\underbrace {\left({a+2bk}\right)e_{c}} _{\rm {carrier}}+\underbrace {2be_{m}e_{c}} _{{\rm {2}}\;{\rm {sidebands}}}+\underbrace {be_{m}^{2}} _{{\rm {2}}\;{\rm {x}}\;{\rm {modulating}}\;{\rm {frequency}}}+\underbrace {be_{c}^{2}} _{{\rm {2}}\;{\rm {x}}\;{\rm {carrier}}\;{\rm {frequency}}}$

调制指数测量

有时很难确定调制指数，特别是对于复杂信号。然而，通过仔细观察，相对容易确定。
有两种实用的方法可以推导出调制指数：

1. 通过在时域中表示 AM 波（使用最大值 - 最小值项）。
2. 通过梯形方法。

梯形示波器显示可以用作确定调制指数。

AM 调制指数：$m={\frac {E_{\max }-E_{\min }}{E_{\max }+E_{\min }}}$

梯形显示使快速识别某些类型的问题成为可能，这将降低 AM 信号质量。

美国 AM 广播的最高授权载波功率为 50 千瓦，尽管定向台允许 52.65 千瓦来补偿相位系统中的损耗。ERP 可以更高

C-QUAM

C-Quam 调制器的基本原理实际上很简单。输出级是普通的 AM 调制器，但载波信号已被幅度限制的矢量调制器取代。因此，限幅器输出实际上是一个相位调制信号。

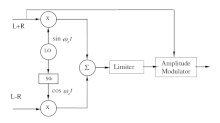
标准 AM 接收机将检测幅度变化为 L+R。立体声接收机还将检测相位变化并提取 L-R。然后它将处理这些信号以分离左右声道。

为了启用立体声解码器，会在 L-R 通道中添加 25 Hz 的导频音。

AM 接收机

如今最常见的接收机是超外差式。它们包括：

• 天线
• 射频放大器
• 本地振荡器和混频器
• 中频部分
• 检波器和放大器

当人们考虑更简单且不足的 TRF 或调谐无线电频率放大器时，可以看出这些子系统的必要性。

TRF 放大器

可以设计一个射频放大器，使其仅接收狭窄频率范围的信号，例如 AM 频段中的一个电台。

通过调整调谐电路的中心频率，可以排除所有其他输入信号。

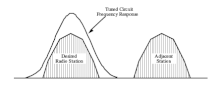
AM 频段范围约为 500 kHz 到 1600 kHz。每个电台需要 10 kHz 的频谱，尽管基带信号仅为 5 kHz。

回想一下，对于一个调谐电路：$Q={\frac {f_{c}}{B}}$。RLC 网络中的中心频率或谐振频率通常通过改变电容值来调整。然而，当中心频率调整时，Q 大致保持不变。这表明随着电路的调谐，带宽随之变化。

例如，在 AM 频段的低端，仅选择一个电台所需的 Q 约为

$Q={\frac {f_{c}}{B}}={\frac {500\;kHz}{10\;kHz}}=50$

当调谐电路调整到 AM 频段的高端时，产生的带宽为

$B={\frac {f_{c}}{Q}}={\frac {1600\;kHz}{50}}=30\;kHz$

如此高的带宽可能会通过三个相邻的电台，从而使有意义的接收变得不可能。

为了防止这种情况，传入的射频信号被混频到一个固定的 IF 或中频，并通过一个恒定带宽的电路。

超外差接收机

射频放大器将射频信号放大到混频器。它具有宽带调谐，不仅放大一个射频电台，而且同时放大多个射频电台。它还会放大任何输入噪声，甚至会贡献一些自身的噪声。

另一个混频器输入是由本地振荡器产生的高频正弦波。在 AM 接收机中，它始终高于所需电台载波频率 455 kHz。理想的混频器将结合传入的载波和本地振荡器以产生和频和差频。

真正的混频器将两个信号组合在一起，并产生大量新的频率

• 直流电平

• 原始两个频率

• 两个输入频率的和与差

• 两个输入频率的谐波

• 所有谐波的和与差

由于射频放大器一次通过多个广播电台，因此混频器输出可能非常复杂。然而，唯一真正感兴趣的信号是所需电台载波频率和本地振荡器频率之间的差值。这个差值频率，也称为 IF（中频），将始终为 455 kHz。通过将它通过以 455 kHz 为中心频率的 10 kHz BPF（带通滤波器），可以消除大部分不需要的信号。

本地振荡器频率

由于混频器产生和频和差频，因此如果本地振荡器高于或低于 IF，则有可能产生 455 kHz IF 信号。不可避免的问题是哪个更可取。

情况一：本地振荡器高于 IF。 这将要求振荡器从 (500 + 455) kHz 调谐到 (1600 + 455) kHz，或大约从 1 MHz 到 2 MHz。通常是调谐 RLC 电路中的电容，它被改变以调整中心频率，而电感保持固定。

由于$f_{c}={\frac {1}{2\pi {\sqrt {LC}}}}$

求解C，我们得到$C={\frac {1}{L\left({2\pi f_{c}}\right)^{2}}}$

当调谐频率最大时，调谐电容最小，反之亦然。由于我们知道要产生的频率范围，我们可以推断出所需的电容范围。

${\frac {C_{\max }}{C_{\min }}}={\frac {L\left({2\pi f_{\max }}\right)^{2}}{L\left({2\pi f_{\min }}\right)^{2}}}=\left({\frac {2\;MHz}{1\;MHz}}\right)^{2}=4$

制造具有 4:1 值变化的电容器是完全可能的。

情况二：本地振荡器低于 IF。 这将要求振荡器从 (500 - 455) kHz 调谐到 (1600 - 455) kHz，或大约从 45 kHz 到 1145 kHz，在这种情况下

${\frac {C_{\max }}{C_{\min }}}=\left({\frac {1145\;kHz}{45\;kHz}}\right)^{2}\approx 648$

制造具有这种范围的可调电容器并不实际。因此，标准 AM 接收机中的本地振荡器高于无线电频段。

镜像频率

就像有两个振荡器频率可以产生相同的 IF 一样，两个不同的电台频率也可以产生 IF。不需要的电台频率被称为镜像频率。

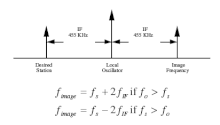
如果无线电前端的任何电路表现出非线性，则有可能其他组合可能会产生中频。一旦镜像频率进入混频器，就无法将其去除，因为它现在被混频到与所需电台相同的 IF 频段。

AM 解调

AM 检测

AM 检测主要分为两种类型：相干检测和非相干检测。其中非相干检测更简单。

• 非相干检测不依赖于载波信号的再生。信息或调制包络可以通过二极管和音频滤波器来移除或检测。
• 相干检测依赖于载波信号的再生，并将再生后的载波信号与 AM 信号混合。这会产生和频和差频。差频对应于原始调制信号。

这两种检测技术都存在一定的缺点。因此，大多数无线电接收机使用这两种技术的结合。

包络检波器

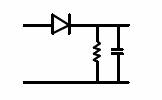
在尝试解调 AM 信号时，似乎只有检查信号的幅度才是合理的。通过仅在任何给定时间检查信号的幅度，我们可以从我们的考虑中去除载波信号，并且我们可以检查原始信号。幸运的是，我们有一个工具可以用来检查信号的幅度：包络检波器。

包络检波器就是一个半波整流器，后面跟着一个低通滤波器。在商用 AM 无线电接收机中，检波器放置在中频段之后。此时载波频率为 455 kHz，而最大包络频率仅为 5 kHz。由于纹波分量几乎是最高基带信号频率的 100 倍，并且不会通过任何后续的音频放大器。

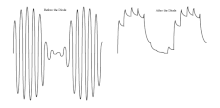
载波频率仅为包络频率 10 倍的 AM 信号将会有相当大的纹波。

同步检波器

在同步检波器或相干检波器中，输入的 AM 信号与原始载波频率混合。

如果你认为这看起来很像一个混频器，你绝对是对的！同步检波器是指两个输入之间的差频为 0 Hz 的检波器。换句话说，两个输入频率相同。让我们检查一下数学。

回想一下，AM 输入在数学上定义为

$e_{am}=\underbrace {\sin \omega _{c}t} _{\rm {Carrier}}+\underbrace {{\frac {m}{2}}\sin \left({\omega _{c}-\omega _{m}}\right)t} _{{\rm {Lower}}\;{\rm {Sideband}}}-\underbrace {{\frac {m}{2}}\sin \left({\omega _{c}+\omega _{m}}\right)t} _{{\rm {Upper}}\;{\rm {Sideband}}}$

在乘法器输出端，我们得到

${\rm {mixer}}\;{\rm {out=}}e_{am}\times \sin \omega _{c}t=\underbrace {-{\frac {m}{2}}\sin \omega _{m}t} _{{\rm {Original}}\;{\rm {Modulation}}\;{\rm {Signal}}}\underbrace {-{\frac {1}{2}}\sin 2\omega _{c}t-{\frac {m}{4}}\sin \left({2\omega _{c}-\omega _{m}}\right)t+{\frac {m}{4}}\sin \left({2\omega _{c}+\omega _{m}}\right)t} _{{\rm {AM}}\;{\rm {signal}}\;{\rm {centered}}\;{\rm {at}}\;{\rm {2}}\;{\rm {times}}\;{\rm {the}}\;{\rm {carrier}}\;{\rm {frequency}}}}$

高频分量可以被滤除，只留下原始的调制信号。

这种技术有一个严重的缺点。问题是如何产生精确的载波频率。如果频率不精确，整个基带信号将被频率差值移动。仅 50 Hz 的偏移将使人声无法识别。可以使用 PLL（锁相环），但要使它在整个 AM 频段内可调并非易事。

因此，大多数无线电接收机使用振荡器来产生固定的中频。然后，中频信号会被包络检波器或固定频率 PLL 处理。

平方检测器

平方检测器也是一种同步或相干检测器。它通过对输入信号进行平方来避免重新生成载波的问题。它本质上利用 AM 信号本身作为一种宽带载波。

乘法器的输出是输入 AM 信号的平方

${\left({e_{am}}\right)^{2}=\left({\sin \omega _{c}t+{\frac {m}{2}}\cos \left({\omega _{c}-\omega _{m}}\right)t-{\frac {m}{2}}\cos \left({\omega _{c}+\omega _{m}}\right)t}\right)^{2}}$

由于输入正在乘以 ${\sin \omega _{c}t}$ 分量，产生的差项之一是原始的调制信号。这种方法的主要困难在于尝试创建一个线性、高频的乘法器。

AM-DSB-SC

AM-DSB-SC 的传输方程如下

$v(t)=As(t)\cos(2\pi f_{c}t)$

需要注意的是，s(t) 可能包含负值。AM-DSB-SC 需要相干接收机，因为调制数据可以为负值，因此接收机需要知道信号是负的（而不仅仅是相移）。AM-DSB-SC 系统对接收端的频移和相移非常敏感。在这个方程式中，A 是传输幅度。

双边带抑制载波调制就是没有广播载波的 AM。回想一下，AM 信号定义为

$e_{am}=\left({1+m\sin \omega _{m}t}\right)\sin \omega _{c}t=\sin \omega _{c}t+{\frac {m_{2}}{2}}\cos \left({\omega _{c}-\omega _{m}}\right)t-{\frac {m_{2}}{2}}\cos \left({\omega _{c}+\omega _{m}}\right)t$

通过从调制信号中去除直流偏移，可以消除频谱中的载波项

$e_{DSBSC}=m\sin \omega _{m}t\sin \omega _{c}t={\frac {m_{2}}{2}}\cos \left({\omega _{c}-\omega _{m}}\right)t-{\frac {m_{2}}{2}}\cos \left({\omega _{c}+\omega _{m}}\right)t$

双平衡环形调制器

双平衡环形调制器是能够创建 DSBSC 的电路之一。

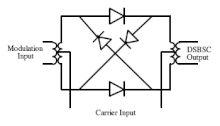
如果载波足够大，导致二极管切换状态，则该电路充当二极管切换调制器。

调制信号以载波速率反转。这本质上是乘以±1。由于变压器不能通过直流，因此没有在乘以时可以创建输出载波的项。由于二极管在任何一个周期都会同样好地切换，因此调制信号实际上被乘以 50% 占空比的方波，从而创建了许多 DSBSC 信号，每个信号都以载波频率的奇数倍为中心。带通滤波器用于提取感兴趣的频率。

一些 IC 平衡调制器使用这种技术，但使用晶体管而不是二极管来执行切换。

推挽平方律平衡调制器

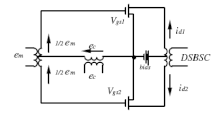
该电路使用与二极管平方律调制器相同的原理。由于直流不能通过变压器，因此可以预期在载波频率处没有输出信号。

漏极电流与栅极-源极电压之间的关系为

$i_{d}=i_{0}+av_{gs}+v_{gs}^{2}$

输出变压器中的净漏极电流由下式给出

$i_{net}=i_{d1}-i_{d2}=i_{0}+av_{gs1}+bv_{gs1}^{2}-\left({i_{0}+av_{gs2}+bv_{gs2}^{2}}\right)$

$i_{net}=a\left({v_{gs1}-v_{gs2}}\right)+b\left({v_{gs1}+v_{gs2}}\right)\left({v_{gs1}-v_{gs2}}\right)$

通过对栅极回路应用 KVL，我们得到

$v_{gs1}={\frac {e_{m}}{2}}+e_{c}\quad \quad \quad \quad v_{gs2}=-{\frac {e_{m}}{2}}+e_{c}$

将所有内容整合在一起，我们得到

$i_{net}=a\left({{\frac {e_{m}}{2}}+e_{c}+{\frac {e_{m}}{2}}-e_{c}}\right)+b\left({{\frac {e_{m}}{2}}+e_{c}-{\frac {e_{m}}{2}}+e_{c}}\right)\left({{\frac {e_{m}}{2}}+e_{c}+{\frac {e_{m}}{2}}-e_{c}}\right)$

$i_{net}=ae_{m}+2be_{c}e_{m}$

由此我们可以注意到，第一项是原始的调制信号，可以很容易地通过高通滤波器过滤掉。第二项的形式为

$\sin \omega _{m}t\sin \omega _{c}t={\frac {1}{2}}\cos \left({\omega _{c}-\omega _{m}}\right)t-{\frac {1}{2}}\cos \left({\omega _{c}+\omega _{m}}\right)t$

即 AM DSBSC。

AM-DSB-C

与 AM-DSB-SC 相比，AM-DSB-C 的特点是以下公式

$v(t)=A[s(t)+c]\cos(2\pi f_{c}t)$

其中 c 是表示载波的正项。如果项 $[s(t)+c]$ 始终非负，我们可以使用简单的包络检波器非相干地接收 AM-DSB-C 信号，从而消除余弦项。+c 项只是一个恒定的直流信号，可以使用阻塞电容器将其消除。

需要注意的是，在 AM-DSB-C 系统中，大量的功率被浪费在传输“增强”的载波频率上。由于载波不包含信息，因此它被认为是浪费的能量。这种方法的优势在于它极大地简化了接收机设计，因为接收机不需要生成相干载波信号。因此，这是传统 AM 无线电中使用的传输方法。

AM-DSB-SC 和 AM-DSB-C 由于都发送两个相同的（但反向的）频率“瓣”或频带，因此在带宽方面都存在缺点。这两个频带（上边带和下边带）完全互为镜像，因此包含相同的信息。为什么我们不能直接切掉其中一个，节省一些带宽呢？答案是我们可以切掉其中一个频带，但并不总是明智之举。切掉其中一个边带的技术称为**幅度调制单边带**（AM-SSB）。AM-SSB 存在一些问题，但也有一些优点。介于 AM-SSB 和两种 AM-DSB 方法之间的折衷方法称为**幅度调制残留边带**（AM-VSB），这种方法使用的带宽比 AM-DSB 方法少，但比 AM-SSB 多。

发射机

典型的 AM-DSB-C 发射机是这样的

             c    cos(...)
             |       |
Signal ---->(+)---->(X)----> AM-DSB-C

它比 AM-DSB-SC 发射机稍微复杂一些。

接收机

AM-DSB-C 接收机非常简单

AM-DSB-C ---->|Envelope Filter|---->|Capacitor|----> Signal

电容器阻挡直流分量，有效地消除了 +c 项。

AM-SSB

为了发送 AM-SSB 信号，我们需要从 AM-DSB 信号中移除一个边带。这意味着我们需要将 AM-DSB 信号通过一个滤波器，以移除一个边带。然而，该滤波器需要是一个非常高阶的滤波器，因为我们需要非常激进的滚降。一个边带需要几乎完全不变地通过滤波器，而另一个边带需要在滤波器处完全停止。

为了解调 AM-SSB 信号，我们需要执行以下步骤

1. 低通滤波器，用于消除噪声
2. 再次用载波频率调制信号
3. 通过另一个滤波器，以消除高频分量
4. 放大信号，因为前面的步骤已经显著衰减了它。

AM-SSB 在带宽方面是最有效的，但在发送和接收这种信号所需的更复杂的硬件方面，存在显著的额外成本。因此，AM-SSB 很少被认为是经济有效的。

单边带是一种 AM 形式，去除了载波和一个边带。在普通的 AM 广播中，发射机根据载波功率来评级。SSB 发射机试图消除载波和其中一个边带。因此，发射机的额定值为 PEP（峰值包络功率）。

$PEP={\frac {\left({{\rm {peak}}\;{\rm {envelope}}\;{\rm {voltage}}}\right)^{2}}{2R_{L}}}$

对于正常的语音信号，SSB发射机输出的功率是PEP的1/4到1/3。

SSB有多种变体。

• SSB - 单边带 - 业余无线电
• SSSC - 单边带抑制载波 - 传输一个小型的导频载波
• ISB - 独立边带 - 两个独立的边带，载波被抑制。用于无线电话。
• VSB - 残留边带 - 部分边带。用于广播电视。
• ACSSB - 幅度压缩SSB

使用SSB有以下几个优势：

• 更有效的频谱利用率

• 较少受到选择性衰落的影响

• 可以将更多功率分配到信息信号中

• 由于带宽限制，可降低10到12 dB的噪声

滤波器方法

创建SSB最简单的方法是生成DSBSC，然后使用带通滤波器提取其中一个边带。

这种技术可以在相对较低的载波频率下使用。在高频下，滤波器的Q值会变得过高。过滤掉一个边带所需的Q值可以用以下公式近似：

$Q\approx {\frac {f_{c}{\sqrt {S}}}{4\Delta f}}$

其中

$f_{c}={\rm {carrier}}\;{\rm {frequency}}$

$\Delta f={\rm {sideband}}\;{\rm {separation}}$

$S={\rm {sideband}}\;{\rm {suppression}}\;{\rm {(not}}\;{\rm {in}}\;{\rm {dB)}}$

几种类型的滤波器用于抑制不需要的边带。

• LC - 最大Q值=200
• 陶瓷 - 最大Q值=2000
• 机械 - 最大Q值=10,000
• 晶体 - 最大Q值=50,000

为了降低对滤波器要求，可以使用双异频技术。

第一个本机振荡器具有相对较低的频率，因此可以移除第一个混频器产生的一个边带。然后信号再次进行异频转换，产生另一对边带。然而，这次它们被足够大的间隙隔开，其中一个可以由带限功率放大器或天线匹配网络移除。

示例

观察以下条件下的频谱分布：

• 音频基带 = 100 Hz 到 5 kHz

• LO1 = 100 kHz

• LO2 = 50 MHz

第一个混频器的频谱输出为：

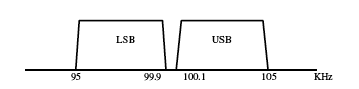
如果所需的边带抑制为80 dB，则过滤掉一个边带所需的Q值大约为：

$S=\log ^{-1}\left({\frac {80}{20}}\right)=10^{4}$

$Q\approx {\frac {f_{c}{\sqrt {S}}}{4\Delta f}}={\frac {100\times 10^{3}{\sqrt {10^{4}}}}{4\times 200}}=12500$

很明显，需要晶体滤波器来去除不需要的边带。

经过滤波器后，只剩下一个边带。在本例中，我们将保留USB。第二个混频器后的频谱为：

通过80 dB抑制一个边带所需的Q值约为：

$Q\approx {\frac {f_{c}{\sqrt {S}}}{4\Delta f}}={\frac {50\times 10^{6}{\sqrt {10^{4}}}}{4\times 200.2\times 10^{3}}}=6244$

因此，我们注意到所需的Q值减半了。

这种 SSB 滤波技术在无线电话应用中使用。

相移法

来自顶部混频器的输出为

$\sin \omega _{m}t\sin \omega _{c}t={\frac {1}{2}}\cos \left({\omega _{c}-\omega _{m}}\right)t-{\frac {1}{2}}\cos \left({\omega _{c}+\omega _{m}}\right)t$

来自底部混频器的输出为

$\cos \omega _{m}t\cos \omega _{c}t={\frac {1}{2}}\cos \left({\omega _{c}-\omega _{m}}\right)t+{\frac {1}{2}}\cos \left({\omega _{c}+\omega _{m}}\right)t$

求和器的输出为

$\cos \left({\omega _{c}-\omega _{m}}\right)t$

对应于下边带。

这种技术的主要困难在于需要在整个输入音频频带上提供恒定的 90^o 相移。为了克服这个障碍，Weaver 或第三种方法使用一个相移的音频子载波。

Weaver 方法

Weaver 或“第三”方法将基带信号放置在低频正交载波上。

这样做的好处是不需要宽带相移器，但是，使用四个混频器使其变得笨拙，而且很少使用。

SSB 发射机

AM-SSB 发射机稍微复杂一些。

          cos(...)
             |
Signal ---->(X)---->|Low-Pass Filter|----> AM-SSB

滤波器必须是高阶滤波器，原因在本章中解释。

SSB 接收机

AM-SSB 接收机也稍微复杂一些。

          cos(...)
             |
AM-SSB ---->(X)---->|Low-Pass Filter|---->|Amplifier|----> Signal

这个滤波器不需要像发射机那样是高阶滤波器。

这些接收机需要极其稳定的振荡器、良好的邻道选择性，通常使用双转换技术。包络检波器不能使用，因为包络以 AM 包络频率的两倍变化。

由于检测到的信号与未发射的载波和瞬时边带之间的差值成正比，因此需要稳定的振荡器。50 Hz 的微小偏移会导致接收到的信号无法使用。

SSB 接收机通常使用固定频率调谐，而不是大多数无线电中发现的连续调谐。晶体振荡器通常用于选择固定频率信道。

AM-VSB

单边带调制对于具有以零频率为中心的能量间隙的信息承载信号（例如，

语音信号）效果良好。但是，对于宽带信号的频谱

有效传输，我们需要寻找一种新的调制方法

有两个原因

• 通常，宽带信号（例如电视视频信号和

计算机数据）的频谱包含大量的低频，这使得使用

SSB 调制变得不切实际。

• 宽带数据的频谱特性适合使用 DSB-SC。但是，DSBSC

需要等于消息带宽两倍的传输带宽，这

违反了带宽节约的要求。

为了克服这两个实际限制，我们需要一种折衷的调制方法

在其频谱特性上介于 SSB 和 DSB-SC 之间。残留边带，

本节将考虑的剩余调制方案，就是这种折衷

方案。

残留边带 (VSB) 调制在两个方面区别于 SSB 调制

实际方面

• 不是完全去除一个边带，而是传输该边带的一部分或残留部分，因此得名“残留边带”。

• 不是完全传输另一个边带，而是几乎传输了该第二个边带的全部。

发射机

这里我们将讨论 AM-VSB 发射机电路。

接收机

这里我们将讨论 AM-VSB 接收机电路。