通信系统/噪声系数

此页面将讨论噪声对传输系统的影响。

噪声类型

大多数人为的电磁噪声出现在 500 MHz 以下的频率。其中最重要的是

• 水力线

• 点火系统

• 荧光灯

• 电机

因此，深空网络被放置在沙漠中，远离这些干扰源。

还有一些自然噪声源，不容易避免，例如

•大气噪声 - 闪电 < 20 MHz

•太阳噪声 - 太阳 - 11 年太阳黑子周期

•宇宙噪声 - 8 MHz 到 1.5 GHz

•热噪声或约翰逊噪声。由于自由电子撞击振动离子而产生。

•白噪声 - 白噪声在指定频率范围内具有恒定的频谱密度。约翰逊噪声是白噪声的一个例子。

•高斯噪声 - 高斯噪声本质上是完全随机的，但是，任何特定幅度值的概率都遵循正态分布曲线。约翰逊噪声本质上是高斯噪声。

•散粒噪声 - 双极型晶体管

$i_{n}={\sqrt {2qI_{dc}\Delta f}}$

其中 q = 电子电荷 1.6 x 10^-19 库仑

•过剩噪声、闪烁噪声、1/f 噪声和粉红噪声 < 1 KHz 与频率成反比，与温度和直流电流成正比

•传输时间噪声 - 发生在电子穿过结的传输时间与信号周期相同时。

在这些噪声中，只有约翰逊噪声可以很容易地分析和补偿。噪声功率由下式给出

$P_{n}=kTB$

其中

k = 玻尔兹曼常数 (1.38 x 10^-23 J/K)

T = 开尔文温度

B = 带宽，单位为 Hz

此方程适用于铜线绕制电阻器，但对于所有电阻器都足够接近。当源阻抗和负载阻抗相等时，会发生最大功率传输。

噪声电压的组合

两个噪声电压的瞬时值只是它们在同一时刻的个体值的总和。

$v_{total\;inst}=v_{1\;inst}+v_{2\;inst}$

此结果在示波器上很容易观察到。但是，它没有特别有用，因为它不会产生像电压表测量的单个稳定的数值。

如果两个电压是相干的 [K = 1]，则总的有效值等于各个有效值的总和。

$v_{total\;rms}=v_{1\;rms}+v_{2\;rms}$

如果两个信号彼此完全随机 [K = 0]，例如约翰逊噪声源，则总功率等于所有各个功率的总和

$P_{total\;random\;noise}=P_{n1\;random}+P_{n2\;random}$

功率为 P = kTB 的约翰逊噪声可以被认为是通过电阻器施加的噪声电压，即戴维南等效。

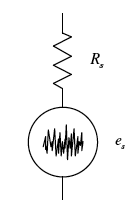
这种噪声源的例子可能是电缆或传输线。从源传递到负载（例如放大器输入）的噪声功率量是源阻抗和负载阻抗的函数。

如果负载阻抗为 0 $\Omega$，则不会向其传输任何功率，因为电压为零。如果负载具有无限的输入阻抗，同样也不会向其传输任何功率，因为没有电流。当源阻抗和负载阻抗相等时，会发生最大功率传输。

$P_{L\;\max }={\frac {e_{s}^{2}}{4R_{s}}}$

在最大功率传输时，有效噪声电压为

$e_{n}={\sqrt {4RP}}={\sqrt {4RkTB}}$

观察如果噪声电阻分解成两个分量会发生什么

$e_{n}^{2}=4RkTB=4\left({R_{1}+R_{2}}\right)kTB=e_{n1}^{2}+e_{n2}^{2}$

由此可见，随机噪声电阻可以直接相加，但随机噪声电压则以矢量方式相加

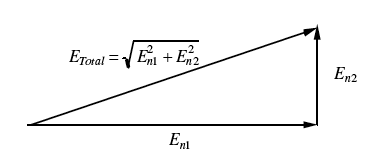
如果噪声源不是完全随机，它们之间存在某种相关性 [0 < K < 1]，则组合结果就不那么容易计算了

$P_{Total\;\left({{\rm {not}}\;{\rm {quite}}\;{\rm {random}}}\right)}={\frac {E_{1}^{2}+E_{2}^{2}+2KE_{1}E_{2}}{R_{0}}}=P_{1}+P_{2}=2K{\sqrt {P_{1}+P_{2}}}$

其中

K = 相关性 [0 < K < 1]

R₀ = 参考阻抗

噪声温度

给定传输介质中的噪声量可以等效为热噪声。热噪声经过充分研究，因此在可能的情况下重复使用相同的方程很有意义。为此，我们可以说，任何数量的辐射噪声都可以用给定有效温度的热噪声来近似。有效温度以开尔文为单位。有效温度通常与标准温度$T_{o}$，即 290 开尔文进行比较。

在微波应用中，很难用电流和电压来描述信号，因为信号更适合用场方程来描述。因此，温度被用来表征噪声。总噪声温度等于所有单个噪声温度的总和。

噪声系数

用来量化噪声的术语可能有点令人困惑，但关键定义是

信噪比：它要么是无量纲的，要么以 dB 为单位。信噪比可以在系统中的任何地方指定。

${\frac {S}{N}}={\frac {{\rm {signal}}\;{\rm {power}}}{{\rm {noise}}\;{\rm {power}}}}={\frac {P_{s}}{P_{n}}}$

$\left({\frac {S}{N}}\right)_{dB}=10\log {\frac {P_{s}}{P_{n}}}$

噪声系数（或噪声比）：$F={\frac {\left({\frac {S}{N}}\right)_{in}}{\left({\frac {S}{N}}\right)_{out}}}$（无量纲）

噪声系数：$NF=10\log F=SNR_{in}-SNR_{out}$ dB

此参数在所有高性能放大器中都有指定，它衡量放大器本身对总噪声的贡献程度。在理想放大器或系统中，NF = 0 dB。本讨论未考虑任何降噪技术，如滤波或动态强调。

Friiss 公式及放大器级联

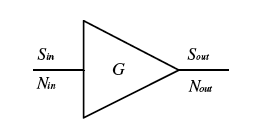
检查放大器级联以了解噪声如何在大型通信系统中累积很有意思。

$F={\frac {\left({\frac {S}{N}}\right)_{in}}{\left({\frac {S}{N}}\right)_{out}}}={\frac {S_{in}}{N_{in}}}\times {\frac {N_{out}}{S_{out}}}$

放大器增益可以定义为：$G={\frac {S_{out}}{S_{in}}}$

因此，输出信号功率为：$S_{out}=GS_{in}$

噪声系数（比）可以改写为：$F={\frac {S_{in}}{N_{in}}}\times {\frac {N_{out}}{GS_{in}}}={\frac {N_{out}}{GN_{in}}}$

输出噪声功率现在可以写成：$N_{out}=FGN_{in}$

从这里我们可以观察到，输入噪声在通过放大器时，会随着噪声系数和放大器增益而增加。一个无噪声放大器将具有1的噪声系数（因子）或0 dB的噪声系数。在这种情况下，输入噪声只会因增益而放大，因为放大器不会产生噪声。

任何系统都可以接收的最小噪声是约翰逊噪声。

$N_{in\left({\rm {minimum}}\right)}=kTB$

因此，任何放大器的输出端可以出现的最小噪声为

$N_{out\left({\rm {minimum}}\right)}=FGkTB$

一个理想放大器的输出噪声将是（F = 1）

$N_{out\left({\rm {perfect}}\right)}=GkTB$

这两个值之间的差异是放大器本身产生的（添加的）噪声。

$N_{out\left({\rm {added}}\right)}=N_{out\left({\rm {minimum}}\right)}-N_{out\left({\rm {perfect}}\right)}=FGkTB-GkTB=\left({F-1}\right)GkTB$

这是出现在输出端的附加（产生的）噪声。

放大器的总输出噪声由下式给出

$N_{total}=N_{out\left({\rm {perfect}}\right)}+N_{out\left({\rm {added}}\right)}=GkTB+\left({F-1}\right)GkTB$

如果再串联一个放大器，总的输出噪声将包含第一级噪声经第二级增益放大后的结果，再加上第二级放大器的附加噪声。

$N_{total}=G_{1}G_{2}kTB+\left({F_{1}-1}\right)G_{1}G_{2}kTB+\left({F_{2}-1}\right)G_{2}kTB$

如果我们将这个表达式的两边除以公因子：$G_{1}G_{2}kTB$

得到

${\frac {N_{total}}{G_{1}G_{2}kTB}}={\frac {G_{1}G_{2}kTB+\left({F_{1}-1}\right)G_{1}G_{2}kTB+\left({F_{2}-1}\right)G_{2}kTB}{G_{1}G_{2}kTB}}$

回顾：$F={\frac {N_{out}}{GN_{in}}}={\frac {N_{total}}{G_{1}G_{2}kTB}}$

因此：$F_{overall}=F_{1}+{\frac {F_{2}-1}{G_{1}}}$

这个过程可以扩展到包含更多级联放大器，从而得出

Friiss 公式

$F=F_{1}+{\frac {F_{2}-1}{G_{1}}}+{\frac {F_{3}-1}{G_{1}G_{2}}}+$

这个公式表明，级联系统的整体噪声系数在很大程度上由第一级放大器的噪声系数决定，因为任何级的噪声贡献都被前面级的增益所划分。这就是为什么任何通信系统中的第一级应该是 LNA (低噪声放大器) 的原因。

接收机灵敏度

在给定的带宽 W 中，我们可以证明噪声功率 N 等于

$N=F(kT_{0})W$

从 N，我们可以证明接收机灵敏度等于

$SNR\times N$