通信系统/有线传输

本页将讨论信号通过物理介质（如电线）传播的主题。

传输线方程

许多类型的通信系统都需要信号在某个点通过铜线传递。

以下分析需要两个假设

• 传输线可以分解成小的、分布式的无源电气元件

• 这些元件与频率无关（即虽然电抗是频率的函数，但电阻、电容和电感不是）

这两个假设将以下分析限制在低 MHz 区域的频率。第二个假设特别难以辩护，因为众所周知，导线的电阻会随着频率的增加而增加，因为导电截面积会减小。这种现象被称为趋肤效应，很难评估。

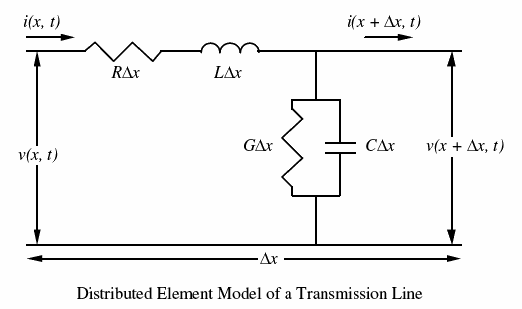
以下数学操作背后的目的是获得一个表达式，该表达式定义了在任何时间（t）沿传输线的任何部分（x）的电压（或电流）。稍后，这种分析将扩展到包括频域。

回想一下电感器和电容器的特征方程

$v=L{\frac {\partial i}{\partial t}}$ 和 $i=C{\frac {\partial v}{\partial t}}$

基尔霍夫电压定律

基尔霍夫电压定律 (KVL) 简而言之，就是在一个闭合回路中，所有电压势的总和等于零。或者换句话说，如果你走上山坡，然后走下山坡，净海拔变化将为零。

在上面的电路中应用 KVL，我们得到

$v\left({x,t}\right)=R\Delta xi\left({x,t}\right)+L\Delta x{\frac {\partial i}{\partial t}}\left({x,t}\right)+v\left({x+\Delta x,t}\right)$

重新排列

$v\left({x,t}\right)-v\left({x+\Delta x,t}\right)=R\Delta xi\left({x,t}\right)+L\Delta x{\frac {\partial i}{\partial t}}\left({x,t}\right)$

但上述方程的 LHS（左侧），表示电缆元件 $\Delta v$ 上的电压降，因此

$\Delta v=R\Delta xi\left({x,t}\right)+L\Delta x{\frac {\partial i}{\partial t}}\left({x,t}\right)$

除以 $\Delta x$，我们得到

${\frac {\Delta v}{\Delta x}}=Ri\left({x,t}\right)+L{\frac {\partial i}{\partial t}}\left({x,t}\right)$

LHS 很容易被识别为导数。简化符号

${\frac {\partial v}{\partial x}}=Ri+L{\frac {\partial i}{\partial t}}$

此表达式包含电流和电压。将方程写成电流或电压作为距离或时间的函数会很方便。

简化方程（相信我）

分离电压和电流的第一步是对位置x求导（**方程式 1**）

${\frac {\partial ^{2}v}{\partial x^{2}}}=R{\frac {\partial i}{\partial x}}+L{\frac {\partial ^{2}i}{\partial x\partial t}}$

下一步是消除电流项，只留下包含电压的表达式。电流沿线的变化等于通过电容C和电导G并联到线的电流。通过在电路中应用 KCL，我们可以获得必要的信息（**方程式 2**）

${\frac {\partial i}{\partial x}}=Gv+C{\frac {\partial v}{\partial t}}$

对时间求导，我们得到（**方程式 3**）

${\frac {\partial ^{2}i}{\partial x\partial t}}=G{\frac {\partial v}{\partial t}}+C{\frac {\partial ^{2}v}{\partial t^{2}}}$

将（**方程式 2**）和（**方程式 3**）代入（**方程式 1**），我们得到所需的简化

${\frac {\partial ^{2}v}{\partial x^{2}}}=R\left[{Gv+C{\frac {\partial v}{\partial t}}}\right]+L\left[{G{\frac {\partial v}{\partial t}}+C{\frac {\partial ^{2}v}{\partial t^{2}}}}\right]$

收集这些项，我们得到

电压的传输线方程

${\frac {\partial ^{2}v}{\partial x^{2}}}=RGv+\left({RC+LG}\right){\frac {\partial v}{\partial t}}+LC{\frac {\partial ^{2}v}{\partial t^{2}}}$

该方程被称为传输线方程。注意，它具有任何特定位置x处的电压作为时间t的函数。

类似地，对于电流，我们得到

电流的传输线方程

${\frac {\partial ^{2}i}{\partial x^{2}}}=RGi+\left({RC+LG}\right){\frac {\partial i}{\partial t}}+LC{\frac {\partial ^{2}i}{\partial t^{2}}}$

但我们还没有完全完成。

求解传输线方程

从历史上看，数学家会通过假设v的解，将其代入方程，并观察结果是否有意义来求解传输线方程中的v。工程师会通过基于一些实验室实验的“有根据的猜测”来遵循类似的程序，关于解可能是什么。如今，有更复杂的技术用于寻找解决方案。在这方面，工程师在寻找数学工具的应用方面可能比数学家落后几个世纪。

为了求解传输线方程，我们将猜测电压函数的解的形式为

$v\left(t\right)=e^{j\omega t}e^{-\gamma x}$

第一项表示一个以角速度 $\omega$ 弧度每秒旋转的单位向量，换句话说，是某个频率的正弦波。第二项表示正弦波被传输线修改，即其幅度随距离呈指数衰减。如果我们让 $\gamma$ 是一个复数，我们也可以包括信号沿线路传播时发生的任何相位变化。

正弦波用作信号源是因为它易于生成并进行数学操作。欧拉恒等式显示了指数表示法和三角函数之间的关系

欧拉恒等式

$e^{j\omega t}=\cos \left({\omega t}\right)+j\sin \left({\omega t}\right)$

回到我们的猜测，我们设 $\gamma =\alpha +j\beta$，因此

$v\left(t\right)=e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}=e^{-\alpha x}e^{\left({\omega t-\beta x}\right)j}$

项 $e^{-\alpha x}$ 表示信号沿线路传播时的指数幅度衰减。 $\alpha$ 称为衰减系数，以每米尼泊尔表示。

项 $e^{\left({\omega t-\beta x}\right)j}$ 表示线路任意点上的信号频率。 $\beta$ 分量称为相移系数，以弧度每米表示。

将我们的猜测

$v\left(t\right)=e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}$

代入电压的传输线方程，我们得到

${\frac {\partial ^{2}}{\partial x^{2}}}\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]=RG\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]+\left({RC+LG}\right){\frac {\partial }{\partial t}}\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]+LC{\frac {\partial ^{2}}{\partial t^{2}}}\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]$

这个公式看起来很吓人，但如果你能进行基本微分和代数运算，你就能解决它！

简化方程式（相信我）

现在我们的目标是逐步进行数学运算，看看能否得到一个合理的解。如果我们得出矛盾的结果或不合理的结论，那就意味着我们的推测是错误的，我们需要进行更多的实验，并提出更好的猜测来解释电压和电流在传输线上的传播方式。

让我们逐项分析这个公式

LHS = RHS Term 1 + RHS Term 2 + RHS Term 3

从左侧 (LHS) 开始，我们得到以下简化结果

${\frac {\partial ^{2}}{\partial x^{2}}}\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]={\frac {\partial }{\partial x}}\left[{-\left({\alpha +j\beta }\right)e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]=\left({\alpha +j\beta }\right)^{2}e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}$

信不信由你，RHS Term 1 不需要简化。

简化 RHS Term 2，我们得到

$\left({RC+LG}\right){\frac {\partial }{\partial t}}\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]=\left({RC+LG}\right)j\omega \left({e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right)$

简化 RHS Term 3，我们得到

$LC{\frac {\partial ^{2}}{\partial t^{2}}}\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]=LC{\frac {\partial }{\partial t}}\left[{j\omega e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]=-LC\omega ^{2}e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}$

让我们把所有东西重新组合在一起

$\left({\alpha +j\beta }\right)^{2}e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}=RG\left({e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right)+\left({RC+LG}\right)j\omega \left({e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right)-LC\omega ^{2}\left({e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right)$

请注意，这四个项中的每一个都包含表达式 $e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}$。

因此，我们最终得到

$\left({\alpha +j\beta }\right)^{2}=RG+\left({RC+LG}\right)j\omega -LC\omega ^{2}$

这可以进一步简化为

衰减和相移系数

$\alpha +j\beta =\gamma ={\sqrt {\left({R+j\omega L}\right)\left({G+j\omega C}\right)}}$

这个结果不矛盾也不不合理。因此，我们得出结论，我们的推测是正确的，我们已经成功地找到了传输线上的衰减和相移的表达式，该表达式是其分布式电气组件和频率的函数。

无损传输线

信号损耗通过两种基本机制发生：信号功率可以在电阻器 [或电导] 中消散，或者信号电流可以通过电抗并联到交流地。在传输线理论中，无损传输线不会消散功率。然而，信号仍然会逐渐衰减，因为并联电抗通过接地路径将电流返回到电源。为了使功率损耗等于零，R = G = 0。当传输线非常短时，会发生这种情况。示波器探头是极短传输线的示例。传输线方程简化为电压方程

${\frac {\partial ^{2}v}{\partial x^{2}}}=LC{\frac {\partial ^{2}v}{\partial t^{2}}}$

和电流方程

${\frac {\partial ^{2}i}{\partial x^{2}}}=LC{\frac {\partial ^{2}i}{\partial t^{2}}}$

为了确定正弦信号如何受到此类线路的影响，我们可以简单地将正弦电压或电流代入上述表达式并像以前一样求解，或者我们可以采用更简单的方法。我们可以从一般情况的解开始

$\alpha +j\beta =\gamma ={\sqrt {\left({R+j\omega L}\right)\left({G+j\omega C}\right)}}$

令 *R* = *G* = 0，并简化

$\alpha +j\beta ={\sqrt {\left({j\omega L}\right)\left({j\omega C}\right)}}=\omega \left({LC}\right)^{2}j$

等式实部和虚部

$\alpha =0$

$\beta =\omega {\sqrt {LC}}$

这个表达式告诉我们，**一个在无损传输线上传播的信号，会经历一个与其频率成正比的相移。**

相速度

一个新的参数，称为相速度，可以从这些变量中提取出来。

$V_{p}={\frac {1}{\sqrt {LC}}}={\frac {\omega }{\beta }}$ 米每秒

相速度是指波前上固定点看起来移动的速度。在导线传输线的情况下，它也是传播速度，通常：0.24c < Vp < 0.9c。

波前上两个相同点之间的距离是波长 ($\lambda$)，因为一个周期被定义为 2$\pi$ 弧度。

$\lambda ={\frac {2\pi }{\beta }}$ 并且 $\omega =2\pi f$

因此

$V_{p}=\lambda f$

在自由空间中，相速度为 3 x 10⁸ 米/秒，即光速。在电缆中，相速度略低，因为信号是由电子传播的。在波导传输线中，相速度超过光速。

无失真传输线

无失真线不会扭曲信号相位，但会引入信号损耗。由于常见的传输线不是超导体，信号幅度会减小，但会保持与输入相同的形状。这种特性对于长电缆系统至关重要。

如果相速度 V_p 在所有频率下保持恒定，则不会发生相位失真。

根据定义，在一个波长 $\lambda$ 上会发生 2$\pi$ 弧度的相移。

由于

$V_{p}=\lambda f\quad \quad \lambda ={\frac {2\pi }{\beta }}\quad \quad f={\frac {\omega }{2\pi }}$

那么

$V_{p}={\frac {2\pi }{\beta }}\times {\frac {\omega }{2\pi }}={\frac {\omega }{\beta }}$

这告诉我们，为了使相速度 V_p 保持恒定，相移系数 $\beta$ 必须与频率 $\omega$ 成正比变化。

回顾

$\gamma ={\sqrt {\left({R+j\omega L}\right)\left({G+j\omega C}\right)}}=\alpha +j\beta$

现在的问题是找到$\beta$. 这可以通过以下步骤完成。

$\gamma ={\sqrt {\left({\frac {R+j\omega L}{j\omega L}}\right)\left({j\omega L}\right)\left({\frac {G+j\omega C}{j\omega C}}\right)\left({j\omega C}\right)}}=j\omega {\sqrt {LC}}{\sqrt {1+{\frac {R}{j\omega L}}}}{\sqrt {1+{\frac {G}{j\omega C}}}}$

看起来我们丢失了$\beta$，但不要放弃。第二和第三个根可以使用二项式展开式展开。

回顾

$\left({1+x}\right)^{n}=1+nx+{\frac {n\left({n-1}\right)}{2!}}x^{2}+{\frac {n\left({n-1}\right)\left({n-2}\right)}{3!}}x^{3}+\cdots$

在本例中，n = 1/2。由于后续项的贡献迅速减小，$\gamma$仅扩展到3项。

$\gamma \approx j\omega {\sqrt {LC}}\left({1+{\frac {1}{2}}{\frac {R}{j\omega L}}-{\frac {1}{8}}\left({\frac {R}{j\omega L}}\right)^{2}}\right)\left({1+{\frac {1}{2}}{\frac {G}{j\omega C}}-{\frac {1}{8}}\left({\frac {G}{j\omega C}}\right)^{2}}\right)$

这看起来可能很复杂，但请记住这只是代数，它最终会简化为简单的优雅形式。展开各项后，我们得到

$\gamma \approx j\omega {\sqrt {LC}}\left\{{\begin{array}{l}1+{\frac {1}{2}}{\frac {G}{j\omega C}}-{\frac {1}{8}}\left({\frac {G}{j\omega C}}\right)^{2}+{\frac {1}{2}}{\frac {R}{j\omega L}}-{\frac {1}{4}}{\frac {RG}{\omega ^{2}LC}}\\-{\frac {1}{16}}{\frac {R}{j\omega L}}\left({\frac {G}{j\omega C}}\right)^{2}-{\frac {1}{8}}\left({\frac {R}{j\omega L}}\right)^{2}\\-{\frac {1}{16}}\left({\frac {R}{j\omega L}}\right)^{2}{\frac {G}{j\omega C}}+{\frac {1}{64}}\left({\frac {R}{j\omega L}}\right)^{2}\left({\frac {G}{j\omega C}}\right)^{2}\\\end{array}}\right\}$

由于 $\gamma =\alpha +j\beta$，我们只需要将实部和虚部等式求解即可得到 $\beta$。

$\beta \approx \omega {\sqrt {LC}}\left\{{1+\underbrace {{\frac {1}{8}}\left({\frac {G}{\omega C}}\right)^{2}-{\frac {1}{4}}{\frac {RG}{\omega ^{2}LC}}+{\frac {1}{8}}\left({\frac {R}{\omega L}}\right)^{2}} _{{\rm {Difference}}\;{\rm {of}}\;{\rm {squares}}}+\underbrace {{\frac {1}{64}}\left({\frac {R}{\omega L}}\right)^{2}\left({\frac {G}{\omega C}}\right)^{2}} _{{\rm {Very}}\;{\rm {small}}}}\right\}$

或者

$\beta \approx \omega {\sqrt {LC}}\left\{{1+{\frac {1}{8}}\left({{\frac {R}{\omega L}}-{\frac {G}{\omega C}}}\right)^{2}}\right\}$

注意，如果 ${\frac {R}{\omega L}}={\frac {G}{\omega C}}$，则 $\beta \approx \omega {\sqrt {LC}}$

从这里我们可以观察到$\beta$ 与$\omega$ 成正比。

因此，无失真传输的必要条件是：

RC = LG

这是宽带同轴电缆网络的基本设计特征之一。

如果我们将实数项等同起来，我们得到

$\alpha \approx {\sqrt {RG}}$

所以学习代数终究是有原因的！

频域

信号分析通常在频域进行。这告诉我们传输线如何影响它们所传输信号的频谱内容。

为了确定这一点，有必要找到传输线方程的傅里叶变换。回想一下

${\frac {\partial ^{2}v}{\partial x^{2}}}=RGv+\left({RC+LG}\right){\frac {\partial v}{\partial t}}+LC{\frac {\partial ^{2}v}{\partial t^{2}}}$

并回想一下（希望如此）傅里叶变换（它将时域转换为频域）

$\mathbb {F} \left\{{f\left(t\right)}\right\}=F\left(\omega \right)=\int \limits _{-\infty }^{\infty }{e^{-j\omega t}f\left(t\right)dt}$

为了防止这种分析“爆炸”，我们必须对电压函数施加一个规定，即它在沿线的无限距离处消失为零。这包括一个基本边界条件。

${\text{let}}\quad v\to 0\quad {\text{as}}\quad x\to \infty$

这个规定与实际的实验室实验相一致。众所周知，信号幅度会随着路径长度的增加而减小。

同样，必须施加一个时间边界条件，即信号在遥远的过去某个时间为零，并且在遥远的未来某个时间也会为零。

${\text{let}}\quad v\to 0\quad {\text{as}}\quad t\to \infty$

尽管工程师在施加这些限制方面没有困难，但数学纯粹主义者却有些反感。出于这个原因和其他原因，已经开发了其他限制较少的变换。在这种情况下最值得注意的是拉普拉斯变换，它没有相同的边界条件。

为了继续我们的分析，我们必须在做出必要的让步之后，找到与以下项相对应的傅里叶变换

$\mathbb {F} \left\{v\right\}\quad \quad \quad \mathbb {F} \left\{{\frac {\partial v}{\partial t}}\right\}\quad \quad \quad \mathbb {F} \left\{{\frac {\partial ^{2}v}{\partial t^{2}}}\right\}$

${\text{Let:}}\quad \quad \quad \mathbb {F} \left\{v\right\}=V$

然后在导数上应用变换，我们得到

$\mathbb {F} \left\{{\frac {\partial v}{\partial t}}\right\}=\int \limits _{-\infty }^{\infty }{e^{-j\omega t}{\frac {\partial v}{\partial t}}dt}$

可以使用分部积分法求解此方程

$\int {u\,dv}=uv-\int {v\,du}$

${\text{let}}\quad u=e^{-j\omega t}\quad \quad \quad \therefore du=-j\omega e^{-j\omega t}$

${\text{and}}\quad dv={\frac {\partial v}{\partial t}}\quad \quad \quad \therefore v=v$

$\therefore \mathbb {F} \left\{{\frac {\partial v}{\partial t}}\right\}=e^{-j\omega t}\left.v\right|_{-\infty }^{\infty }-\int \limits _{-\infty }^{\infty }{v\left({-j\omega e^{-j\omega t}}\right)dt}$

当 t 趋于无穷大时，应用边界条件使第一项消失。

$\therefore \mathbb {F} \left\{{\frac {\partial v}{\partial t}}\right\}=j\omega \int \limits _{-\infty }^{\infty }{e^{-j\omega t}v\,dt}$

注意，得到的积分只是傅里叶变换。换句话说

$\mathbb {F} \left\{{\frac {\partial v}{\partial t}}\right\}=j\omega \mathbb {F} \left\{v\right\}=j\omega V$

类似地

$\mathbb {F} \left\{{\frac {\partial ^{2}v}{\partial t^{2}}}\right\}=\left({j\omega }\right)^{2}\mathbb {F} \left\{v\right\}=\left({j\omega }\right)^{2}V$

现在我们可以将传输线方程写成频域形式

${\frac {\partial ^{2}V}{\partial x^{2}}}=RGV+\left({RC+LG}\right)j\omega V+LC\left({j\omega }\right)^{2}V$

其中

$V=V\left(\omega \right)=\mathbb {F} \left\{{v\left(t\right)}\right\}$

重新排列这些项，我们得到

${\frac {\partial ^{2}V}{\partial x^{2}}}=\left[{RG+\left({RC+LG}\right)j\omega +\left({j\omega L}\right)\left({j\omega C}\right)}\right]V$

或者

${\frac {\partial ^{2}V}{\partial x^{2}}}=\left[{\left({R+j\omega L}\right)\left({G+j\omega C}\right)}\right]V$

因为

${\sqrt {\left({R+j\omega L}\right)\left({G+j\omega C}\right)}}=\alpha +j\beta =\gamma$

那么

${\frac {\partial ^{2}V}{\partial x^{2}}}=\gamma ^{2}V$

或者

${\frac {\partial ^{2}V}{\partial x^{2}}}-\gamma ^{2}V=0$

这代表了频域中传输线方程最一般的形式。现在必须求解此方程以观察电压（或电流）如何随距离和频率变化。这可以通过假设以下形式的解来完成

$V=\underbrace {Ae^{-\gamma x}} _{{\text{forward}}\;{\text{wave}}}+\underbrace {Be^{\gamma x}} _{{\text{reverse}}\;{\text{wave}}}$

这些项表示信号沿着传输线传播时呈指数衰减。如果我们忽略任何反射，假设电缆无限长或正确端接，则简化为

$V=V_{0}e^{-\gamma x}$

为了验证此假设是否正确，将其代入方程，看看是否出现矛盾。如果没有矛盾，那么我们的假设构成一个有效的解。

${\frac {\partial ^{2}}{\partial x^{2}}}V_{0}e^{-\gamma x}-\gamma ^{2}V_{0}e^{-\gamma x}=0$

${\frac {\partial }{\partial x}}\left({-\gamma ^{2}V_{0}e^{-\gamma x}}\right)-\gamma ^{2}V_{0}e^{-\gamma x}=0$

$\gamma ^{2}V_{0}e^{-\gamma x}-\gamma ^{2}V_{0}e^{-\gamma x}=0$

$0=0$

因此我们验证了假设的解。这告诉我们，在频域中，传输线上的电压或电流呈指数衰减

$V=V_{0}e^{-\gamma x}$

其中

$\gamma ={\sqrt {\left({R+j\omega }\right)\left({G+j\omega }\right)}}=\left|\gamma \right|\angle \varphi =\alpha +j\beta$

$\gamma ={\text{ propagation}}\;{\text{constant}}$

$\alpha ={\text{ attenuation}}\;{\text{coeficient}}$

$\beta ={\text{phase}}\;{\text{coefficient}}$

在指数形式中，正弦波可以用一个以一定频率旋转的单位矢量来表示

$e^{j\omega t}=\cos \omega t+j\sin \omega t$

请注意，该函数的幅度为 1，但相位角随 *t* 的变化而变化。

如果我们令： $V_{0}=e^{j\omega t}$

那么： $V_{0}=e^{j\omega t}e^{-\gamma x}=e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}=\underbrace {e^{-\alpha x}} _{{\text{attenuation}}\;vs.\;x}\overbrace {e^{j\left({\omega t-\beta x}\right)}} ^{{\text{phase}}\;vs{\text{.}}\;t\;{\text{and}}\;x}$

这个结果非常有趣，因为它与时域传输线方程的解相同。项 ${e^{-\alpha x}}$ 表示指数衰减。随着长度 *x* 的增加，信号被衰减。衰减量定义为

以尼培表示的衰减： $N=\left|{\ln e^{-\alpha x}}\right|=\alpha x$

以 dB 表示的衰减： $=20\log e^{-\alpha x}\approx 8.68589\alpha x$

这使我们能够在知道传输线的基本线参数 *R, L, G* 和 *C* 的情况下，确定传输线中任何点上的任何频率的衰减量。

项 ${e^{j\left({\omega t-\beta x}\right)}}$ 表示一个旋转的单位矢量，因为

$e^{j\left({\omega t-\beta x}\right)}=\cos \left({\omega t-\beta x}\right)+j\sin \left({\omega t-\beta x}\right)$

该矢量的相位角为 ${\beta x}$ 弧度。

特性阻抗

传输线的特性阻抗也称为冲击阻抗，不要与它的电阻混淆。即使线路无限长，电信号仍然会沿着它传播，尽管电阻趋于无穷大。特性阻抗是由其交流属性决定的，而不是直流属性。

回顾我们之前的分析