交换代数/函子、自然变换、泛函箭头

函子

定义

有两种类型的函子，协变函子和反变函子。通常，协变函子简称为函子。

定义 2.1:

设 ${\mathcal {C}},{\mathcal {D}}$ 是两个范畴。 协变函子 $F:{\mathcal {C}}\to {\mathcal {D}}$ 将

• 每个对象 $A$ 关联到 ${\mathcal {C}}$ 中的一个对象 $F(A)$ ${\mathcal {D}}$，并且
• 每个态射 $f:A\to B$ 关联到 ${\mathcal {C}}$ 中的一个态射 $F(f):F(A)\to F(B)$，

使得以下规则满足

1. 对于 ${\mathcal {C}}$ 中的所有对象 $A$，我们有 $F(1_{A})=1_{F(A)}$，并且
2. 对于所有态射 $f:A\to B$ 和 $g:B\to C$ 属于 ${\mathcal {C}}$ ，我们有 $F(g\circ f)=F(g)\circ F(f)$。

定义 2.2:

设 ${\mathcal {C}},{\mathcal {D}}$ 为两个范畴。一个 逆变函子 $F:{\mathcal {C}}\to {\mathcal {D}}$ 将

• 每个对象 $A$ 关联到 ${\mathcal {C}}$ 中的一个对象 $F(A)$ ${\mathcal {D}}$，并且
• 每个态射 $f:A\to B$ 映射到 ${\mathcal {C}}$ 中的一个态射 $F(f):F(B)\to F(A)$，

使得以下规则满足

1. 对于 ${\mathcal {C}}$ 中的所有对象 $A$，我们有 $F(1_{A})=1_{F(A)}$，并且
2. 对于所有态射 $f:A\to B$ 和 $g:B\to C$ 属于 ${\mathcal {C}}$ ，我们有 $F(g\circ f)=F(f)\circ F(g)$。

遗忘函子

我不确定是否有遗忘函子的精确定义，但事实上，信不信由你，这个概念很容易通过几个例子来解释。

例子 2.3:

考虑以同态为态射的群范畴。我们可以定义一个函子，将每个群映射到它的底层集合，并将每个同态映射到它自身作为函数。这是一个从群范畴到集合范畴的函子。由于该函子的目标对象缺少群结构，因此群结构已被遗忘，因此这里我们处理的是一个遗忘函子。

例子 2.4:

考虑环范畴。请记住，每个环关于加法运算都是一个阿贝尔群。因此，我们可以定义一个从环范畴到群范畴的函子，将每个环映射到它的底层群。这也是一个遗忘函子；它忘记了环的乘法。

自然变换

定义 2.5:

设${\mathcal {C}},{\mathcal {D}}$ 是范畴，并设 $F,G:{\mathcal {C}}\to {\mathcal {D}}$ 是两个函子。一个 **自然变换** 是 ${\mathcal {D}}$ 中的一族态射 $\eta _{X}:F(X)\to G(X)$，其中 $X$ 取遍 ${\mathcal {C}}$ 中的所有对象，这些态射与 ${\mathcal {C}}$ 中态射 $f:X\to Y$ 在函子 $F$ 和 $G$ 作用下的图像相容；也就是说，下面的图是可交换的

例 2.6:

设${\mathcal {C}}$ 是所有域的范畴，而${\mathcal {D}}$ 是所有环的范畴。我们定义一个函子

$F:{\mathcal {C}}\to {\mathcal {D}}$

如下：${\mathcal {C}}$ 中的每个对象 $\mathbb {F}$ 将被映射到环 $R_{\mathbb {F} }$，该环由域继承的加法和乘法组成，其底层集合是元素

$S_{\mathbb {F} }\{\overbrace {1_{\mathbb {F} }+1_{\mathbb {F} }+\cdots +1_{\mathbb {F} }} ^{n{\text{ times}}}|n\in \mathbb {N} _{0}\}\cup \{\overbrace {-1_{\mathbb {F} }-1_{\mathbb {F} }-\cdots -1_{\mathbb {F} }} ^{n{\text{ times}}}|n\in \mathbb {N} \}$,

其中 $1_{\mathbb {F} }$ 是域 $\mathbb {F}$ 的单位元。 任何域的态射 $f:\mathbb {F} \to \mathbb {G}$ 将被映射到限制 $f\upharpoonright _{S_{\mathbb {F} }}$； 注意，这是定义良好的（即，映射到与 $\mathbb {G}$ 相关的对象，在函子 $F$ 下），因为

$f(1_{\mathbb {F} }+1_{\mathbb {F} }+\cdots +1_{\mathbb {F} })=f(1_{\mathbb {F} })+f(1_{\mathbb {F} })+\cdots +f(1_{\mathbb {F} })=1_{\mathbb {G} }+1_{\mathbb {G} }+\cdots +1_{\mathbb {G} }$

以及

$f(-1_{\mathbb {F} }-1_{\mathbb {F} }-\cdots -1_{\mathbb {F} })=-f(1_{\mathbb {F} })-f(1_{\mathbb {F} })-\cdots -f(1_{\mathbb {F} })=-1_{\mathbb {G} }-1_{\mathbb {G} }-\cdots -1_{\mathbb {G} }$,

其中 $1_{\mathbb {G} }$ 是域 $\mathbb {G}$ 的单位。

我们进一步定义了一个函子

$G:{\mathcal {C}}\to {\mathcal {D}}$,

将每个域 $\mathbb {F}$ 映射到其关联的 素域 $\mathbb {F} _{\text{prime}}$，将其视为一个环，然后再次限制态射，即，将每个态射 $f:\mathbb {F} \to \mathbb {G}$ 映射到 $f\upharpoonright _{\mathbb {F} _{\text{prime}}}$（这根据与上面相同的计算以及注意到 $f$ 是域态射，将逆映射到逆而定义）。

在这个设置中，映射

$\eta _{\mathbb {F} }:R_{\mathbb {F} }\to \mathbb {F} _{\text{prime}}$,

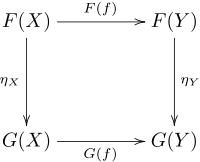
由包含给出，形成从 $F$ 到 $G$ 的自然变换；这可以通过直接检查交换图来验证。

泛箭头

定义 2.7（泛箭头）:

设 ${\mathcal {C}},{\mathcal {D}}$ 为范畴，设 $F:{\mathcal {C}}\to {\mathcal {D}}$ 为一个函子，设 $Y$ 为 ${\mathcal {D}}$ 中的一个对象。**泛映射**是一个态射 $g:Y\to F(X)$，其中 $X$ 是 ${\mathcal {C}}$ 中的一个固定对象，使得对于 ${\mathcal {C}}$ 中的任何其他对象 $Z$ 和态射 $h:Y\to F(Z)$，都存在唯一态射 $f:X\to Z$ 使得该图

可交换。