定义 21.1 :
令 X {\displaystyle X} X {\displaystyle X} 不可约 当且仅当 X {\displaystyle X}
有些人(拓扑学家)将不可约空间称为超连通 空间。
证明 1 : 我们证明 1. ⇒ {\displaystyle \Rightarrow } ⇒ {\displaystyle \Rightarrow } ⇒ {\displaystyle \Rightarrow } ⇒ {\displaystyle \Rightarrow }
1. ⇒ {\displaystyle \Rightarrow } X = A ∪ B {\displaystyle X=A\cup B} A {\displaystyle A} B {\displaystyle B} O := X ∖ A {\displaystyle O:=X\setminus A} U := X ∖ B {\displaystyle U:=X\setminus B} O , U {\displaystyle O,U}
O ∩ U = ( X ∖ A ) ∩ ( X ∖ B ) = X ∖ ( A ∪ B ) = ∅ {\displaystyle O\cap U=(X\setminus A)\cap (X\setminus B)=X\setminus (A\cup B)=\emptyset } 根据德摩根定律之一,这与 1 矛盾。
2. ⇒ {\displaystyle \Rightarrow } U ⊆ X {\displaystyle U\subseteq X} A := U ¯ {\displaystyle A:={\overline {U}}} X {\displaystyle X} B := X ∖ U {\displaystyle B:=X\setminus U} X = A ∪ B {\displaystyle X=A\cup B}
3. ⇒ {\displaystyle \Rightarrow } ∅ ≠ A ⊊ X {\displaystyle \emptyset \neq A\subsetneq X} A ∘ ≠ ∅ {\displaystyle {\overset {\circ }{A}}\neq \emptyset } A ∘ ¯ ⊆ A {\displaystyle {\overline {\overset {\circ }{A}}}\subseteq A} A ∘ {\displaystyle {\overset {\circ }{A}}}
4. ⇒ {\displaystyle \Rightarrow } O , U ⊆ X {\displaystyle O,U\subseteq X} O ∩ U = ∅ {\displaystyle O\cap U=\emptyset } A := X ∖ O {\displaystyle A:=X\setminus O} A {\displaystyle A} X {\displaystyle X} O ⊆ X ∖ A {\displaystyle O\subseteq X\setminus A} O ⊆ A ∘ {\displaystyle O\subseteq {\overset {\circ }{A}}} A {\displaystyle A} ◻ {\displaystyle \Box }
证明 2 : 我们证明 1. ⇒ {\displaystyle \Rightarrow } ⇒ {\displaystyle \Rightarrow } ⇒ {\displaystyle \Rightarrow } ⇒ {\displaystyle \Rightarrow }
1. ⇒ {\displaystyle \Rightarrow } X {\displaystyle X} A {\displaystyle A} X ∖ A {\displaystyle X\setminus A} A ∘ {\displaystyle {\overset {\circ }{A}}} X {\displaystyle X}
4. ⇒ {\displaystyle \Rightarrow } O ⊆ X {\displaystyle O\subseteq X} O {\displaystyle O} X {\displaystyle X} O ¯ {\displaystyle {\overline {O}}} X {\displaystyle X}
3. ⇒ {\displaystyle \Rightarrow } X = A ∪ B {\displaystyle X=A\cup B} A , B ⊊ X {\displaystyle A,B\subsetneq X} O := X ∖ B {\displaystyle O:=X\setminus B} A ⊃ O {\displaystyle A\supset O} O {\displaystyle O} X {\displaystyle X}
2. ⇒ {\displaystyle \Rightarrow } O , U ⊆ X {\displaystyle O,U\subseteq X} X = ( X ∖ O ) ∪ ( X ∖ U ) {\displaystyle X=(X\setminus O)\cup (X\setminus U)} ◻ {\displaystyle \Box }
剩余的箭头 :
1. ⇒ {\displaystyle \Rightarrow } U ⊂ X {\displaystyle U\subset X} X ∖ U ¯ {\displaystyle X\setminus {\overline {U}}} U {\displaystyle U}
3. ⇒ {\displaystyle \Rightarrow } O , U ⊆ X {\displaystyle O,U\subseteq X} O ⊆ X ∖ U {\displaystyle O\subseteq X\setminus U} O {\displaystyle O}
2. ⇒ {\displaystyle \Rightarrow } A ⊊ X {\displaystyle A\subsetneq X} X = A ∪ ( X ∖ A ∘ ) {\displaystyle X=A\cup (X\setminus {\overset {\circ }{A}})}
4. ⇒ {\displaystyle \Rightarrow } X = A ∪ B {\displaystyle X=A\cup B} A , B ⊊ X {\displaystyle A,B\subsetneq X} ∅ ≠ X ∖ A ⊆ A ∘ {\displaystyle \emptyset \neq X\setminus A\subseteq {\overset {\circ }{A}}}
我们接下来将证明不可约空间的几个性质。
定理 21.3 :
每个不可约空间 X {\displaystyle X}
证明 :
1. 连通性: 假设 X = U ∪ ˙ O {\displaystyle X=U{\dot {\cup }}O} U , O {\displaystyle U,O}
2. 局部连通性: 令 x ∈ V ⊆ X {\displaystyle x\in V\subseteq X} V {\displaystyle V} X {\displaystyle X} ◻ {\displaystyle \Box }
定理 21.4 :
设 X {\displaystyle X} X {\displaystyle X} | X | ≤ 1 {\displaystyle |X|\leq 1}
证明 :
如果 | X | ≤ 1 {\displaystyle |X|\leq 1} X {\displaystyle X} X {\displaystyle X} x ≠ y {\displaystyle x\neq y} U x , U y ⊆ X {\displaystyle U_{x},U_{y}\subseteq X} x ∈ U x {\displaystyle x\in U_{x}} y ∈ U y {\displaystyle y\in U_{y}} U x ∩ U y = ∅ {\displaystyle U_{x}\cap U_{y}=\emptyset } ◻ {\displaystyle \Box }
定理 21.5 :
设 X , Y {\displaystyle X,Y} X {\displaystyle X} f : X → Y {\displaystyle f:X\to Y} f ( X ) {\displaystyle f(X)} Y {\displaystyle Y}
证明 :设 O , U {\displaystyle O,U} f ( X ) {\displaystyle f(X)} O = f ( X ) ∩ V {\displaystyle O=f(X)\cap V} U = f ( X ) ∩ W {\displaystyle U=f(X)\cap W} V , W ⊆ Y {\displaystyle V,W\subseteq Y}
f − 1 ( O ) = f − 1 ( f ( X ) ∩ V ) = f − 1 ( V ) {\displaystyle f^{-1}(O)=f^{-1}(f(X)\cap V)=f^{-1}(V)} f − 1 ( U ) = f − 1 ( W ) {\displaystyle f^{-1}(U)=f^{-1}(W)} 因此, f − 1 ( O ) {\displaystyle f^{-1}(O)} f − 1 ( U ) {\displaystyle f^{-1}(U)} X {\displaystyle X} x ∈ f − 1 ( O ) {\displaystyle x\in f^{-1}(O)} f ( x ) ∈ O {\displaystyle f(x)\in O} f ( x ) ∉ U {\displaystyle f(x)\notin U} y ∈ O {\displaystyle y\in O} O ⊂ f ( X ) {\displaystyle O\subset f(X)} y = f ( x ) {\displaystyle y=f(x)} x ∈ X {\displaystyle x\in X} x ∈ f − 1 ( O ) {\displaystyle x\in f^{-1}(O)} ◻ {\displaystyle \Box }
推论 21.6 :
如果 X {\displaystyle X} Y {\displaystyle Y} f : X → Y {\displaystyle f:X\to Y} f {\displaystyle f}
证明 :由定理 21.4 和 21.5 可得。 ◻ {\displaystyle \Box }
现在我们可以将不可约空间与诺特空间联系起来。
证明 :
首先我们证明存在性。令 A ⊆ X {\displaystyle A\subseteq X} A {\displaystyle A} A {\displaystyle A} A = B 1 ∪ B 2 {\displaystyle A=B_{1}\cup B_{2}} B 1 {\displaystyle B_{1}} B 2 {\displaystyle B_{2}} 真 闭子集的并集。由于 X {\displaystyle X}
接下来,我们证明唯一性(直至阶数)。设 A = B 1 ∪ ⋯ ∪ B n = C 1 ∪ ⋯ ∪ C m {\displaystyle A=B_{1}\cup \cdots \cup B_{n}=C_{1}\cup \cdots \cup C_{m}} k ∈ { 1 , … , n } {\displaystyle k\in \{1,\ldots ,n\}} B k = ( B k ∩ C 1 ) ∪ ⋯ ∪ ( B k ∩ C m ) {\displaystyle B_{k}=(B_{k}\cap C_{1})\cup \cdots \cup (B_{k}\cap C_{m})} j ∈ { 1 , … , m } {\displaystyle j\in \{1,\ldots ,m\}} B k ⊆ C j ⇔ B k = ( B k ∩ C j ) {\displaystyle B_{k}\subseteq C_{j}\Leftrightarrow B_{k}=(B_{k}\cap C_{j})} S 1 := ( B k ∩ C 1 ) {\displaystyle S_{1}:=(B_{k}\cap C_{1})}
S l + 1 := S l ∪ ( B k ∩ C l + 1 ) {\displaystyle S_{l+1}:=S_{l}\cup (B_{k}\cap C_{l+1})} for 1 ≤ l < m {\displaystyle 1\leq l<m} l = 1 {\displaystyle l=1} l {\displaystyle l} S l ∪ ( B k ∩ C l + 1 ) {\displaystyle S_{l}\cup (B_{k}\cap C_{l+1})} B k {\displaystyle B_{k}} l {\displaystyle l} l {\displaystyle l} S l ∪ ( B k ∩ C l + 1 ) = B k {\displaystyle S_{l}\cup (B_{k}\cap C_{l+1})=B_{k}} j ∈ { 1 , … , m } {\displaystyle j\in \{1,\ldots ,m\}} B k ⊆ C j {\displaystyle B_{k}\subseteq C_{j}} B k {\displaystyle B_{k}} C j {\displaystyle C_{j}} C j {\displaystyle C_{j}} B k ′ {\displaystyle B_{k'}} ⊆ {\displaystyle \subseteq } B k ⊆ B k ′ {\displaystyle B_{k}\subseteq B_{k'}} k = k ′ {\displaystyle k=k'} C j = B k {\displaystyle C_{j}=B_{k}} k {\displaystyle k} σ ( k ) = j {\displaystyle \sigma (k)=j} j {\displaystyle j} j {\displaystyle j} C {\displaystyle C} τ ( j ) = k {\displaystyle \tau (j)=k} B k = C j {\displaystyle B_{k}=C_{j}} τ {\displaystyle \tau } σ {\displaystyle \sigma } n = m {\displaystyle n=m} σ {\displaystyle \sigma } ◻ {\displaystyle \Box }
习题 21.1.1 :设 X {\displaystyle X} O ⊆ X {\displaystyle O\subseteq X} O {\displaystyle O}
定义 21.8 :
设 F {\displaystyle \mathbb {F} }
V ( S ) := { ( x 1 , … , x n ) ∈ F n | ∀ f ∈ S : f ( x 1 , … , x n ) = 0 } {\displaystyle V(S):=\{(x_{1},\ldots ,x_{n})\in \mathbb {F} ^{n}|\forall f\in S:f(x_{1},\ldots ,x_{n})=0\}} 其中 S {\displaystyle S} n {\displaystyle n} F {\displaystyle \mathbb {F} } S ⊆ F [ x 1 , … , x n ] {\displaystyle S\subseteq \mathbb {F} [x_{1},\ldots ,x_{n}]} 代数集 。如果 S = { f } {\displaystyle S=\{f\}} f ∈ F [ x 1 , … , x n ] {\displaystyle f\in \mathbb {F} [x_{1},\ldots ,x_{n}]}
V ( f ) := V ( { f } ) {\displaystyle V(f):=V(\{f\})}
下图描绘了三个代数集(除了 立方体线)。
橙色表面是集合 V ( f 1 ) {\displaystyle V(f_{1})} V ( f 2 ) {\displaystyle V(f_{2})} V ( { f 1 , f 2 } ) {\displaystyle V(\{f_{1},f_{2}\})}
f 1 ( x , y , z ) = z + y 3 {\displaystyle f_{1}(x,y,z)=z+y^{3}} f 2 ( x , y , z ) = x + z 2 {\displaystyle f_{2}(x,y,z)=x+z^{2}} 三个直接的引理是显而易见的。
引理 21.9 :
S ⊆ T ⇒ V ( T ) ⊆ V ( S ) {\displaystyle S\subseteq T\Rightarrow V(T)\subseteq V(S)} 证明 :处于 V ( T ) {\displaystyle V(T)} ◻ {\displaystyle \Box }
引理 21.10(代数集的公式) :
令 F {\displaystyle \mathbb {F} } R := F [ x 1 , … , x n ] {\displaystyle R:=\mathbb {F} [x_{1},\ldots ,x_{n}]} F n {\displaystyle \mathbb {F} ^{n}}
V ( S ) = V ( ⟨ S ⟩ ) {\displaystyle V(S)=V(\langle S\rangle )} S ⊆ R {\displaystyle S\subseteq R} V ( R ) = ∅ {\displaystyle V(R)=\emptyset } V ( ∅ ) = F n {\displaystyle V(\emptyset )=\mathbb {F} ^{n}} V ( I 1 ) ∪ ⋯ ∪ V ( I k ) = V ( I 1 ∩ ⋯ ∩ I k ) {\displaystyle V(I_{1})\cup \cdots \cup V(I_{k})=V(I_{1}\cap \cdots \cap I_{k})} I 1 , … , I k ≤ R {\displaystyle I_{1},\ldots ,I_{k}\leq R} ⋂ j ∈ J V ( S j ) = V ( ⋃ j ∈ J S j ) {\displaystyle \bigcap _{j\in J}V(S_{j})=V\left(\bigcup _{j\in J}S_{j}\right)} S j ⊆ R {\displaystyle S_{j}\subseteq R} 证明 :
1. 令 i := ∑ j = 1 k r j s j ∈ ⟨ S ⟩ {\displaystyle i:=\sum _{j=1}^{k}r_{j}s_{j}\in \langle S\rangle } x = ( x 1 , … , x n ) ∈ V ( S ) {\displaystyle x=(x_{1},\ldots ,x_{n})\in V(S)} i ( x ) = 0 {\displaystyle i(x)=0} ⊆ {\displaystyle \subseteq }
2. V ( R ) = ∅ {\displaystyle V(R)=\emptyset } R {\displaystyle R} V ( ∅ ) {\displaystyle V(\emptyset )} F n {\displaystyle \mathbb {F} ^{n}}
3. ⊆ {\displaystyle \subseteq }
x ∈ V ( I 1 ) ∪ ⋯ ∪ V ( I k ) ⇒ ∃ j ∈ { 1 , … , k } : x ∈ V ( I j ) ⇒ ∀ f ∈ I j : f ( x ) = 0 ⇒ ∀ f ∈ I 1 ∩ ⋯ ∩ I k : f ( x ) = 0 , {\displaystyle {\begin{aligned}x\in V(I_{1})\cup \cdots \cup V(I_{k})&\Rightarrow \exists j\in \{1,\ldots ,k\}:x\in V(I_{j})\\&\Rightarrow \forall f\in I_{j}:f(x)=0\\&\Rightarrow \forall f\in I_{1}\cap \cdots \cap I_{k}:f(x)=0,\end{aligned}}} 因为很明显 I 1 ∩ ⋯ ∩ I k ⊆ I j {\displaystyle I_{1}\cap \cdots \cap I_{k}\subseteq I_{j}}
我们首先证明 ⊇ {\displaystyle \supseteq } k = 2 {\displaystyle k=2} x ∉ V ( I 1 ) ∪ V ( I 2 ) {\displaystyle x\notin V(I_{1})\cup V(I_{2})} x ∈ V ( I 1 ) {\displaystyle x\in V(I_{1})} x ∈ V ( I 2 ) {\displaystyle x\in V(I_{2})} f ∈ I 1 {\displaystyle f\in I_{1}} f ( x ) ≠ 0 {\displaystyle f(x)\neq 0} g ∈ S 2 {\displaystyle g\in S_{2}} g ( x ) ≠ 0 {\displaystyle g(x)\neq 0} f ⋅ g {\displaystyle f\cdot g} I 1 ∩ I 2 {\displaystyle I_{1}\cap I_{2}} ( f ⋅ g ) ( x ) = f ( x ) ⋅ g ( x ) ≠ 0 {\displaystyle (f\cdot g)(x)=f(x)\cdot g(x)\neq 0} x ∉ V ( I 1 ∩ I 2 ) {\displaystyle x\notin V(I_{1}\cap I_{2})}
假设 ⊇ {\displaystyle \supseteq } k − 1 {\displaystyle k-1}
V ( I 1 ∩ ⋯ ∩ I k ) = V ( ( I 1 ∩ ⋯ I k − 1 ) ∩ I k ) ⊆ V ( I 1 ∩ ⋯ I k − 1 ) ∪ V ( I k ) ⊆ V ( I 1 ) ∪ ⋯ ∪ V ( I k − 1 ) ∪ V ( I k ) {\displaystyle V(I_{1}\cap \cdots \cap I_{k})=V((I_{1}\cap \cdots I_{k-1})\cap I_{k})\subseteq V(I_{1}\cap \cdots I_{k-1})\cup V(I_{k})\subseteq V_{(}I_{1})\cup \cdots \cup V(I_{k-1})\cup V(I_{k})} 4.
x ∈ ⋂ j ∈ J V ( S j ) ⇔ ∀ j ∈ J : x ∈ V ( S j ) ⇔ ∀ j ∈ J : ∀ f ∈ S j : f ( x ) = 0 ⇔ ∀ f ∈ ⋃ j ∈ J S j : f ( x ) = 0 ⇔ x ∈ V ( ⋃ j ∈ J S j ) . {\displaystyle {\begin{aligned}x\in \bigcap _{j\in J}V(S_{j})&\Leftrightarrow \forall j\in J:x\in V(S_{j})\\&\Leftrightarrow \forall j\in J:\forall f\in S_{j}:f(x)=0\\&\Leftrightarrow \forall f\in \bigcup _{j\in J}S_{j}:f(x)=0\\&\Leftrightarrow x\in V\left(\bigcup _{j\in J}S_{j}\right).\end{aligned}}} ◻ {\displaystyle \Box } 从这个引理我们可以看出,代数集构成拓扑的闭集,就像我们在第 14 章中了解的扎里斯基闭集一样。我们很快就会找到这个拓扑的名称,但我们首先将以不同的方式定义它,以证明我们将要给出的名称是合理的。
引理 21.11 :
令 F {\displaystyle \mathbb {F} } I ⊆ F [ x 1 , … , x n ] {\displaystyle I\subseteq \mathbb {F} [x_{1},\ldots ,x_{n}]}
V ( I ) = V ( r ( I ) ) {\displaystyle V(I)=V(r(I))} 我们回忆一下 r ( I ) {\displaystyle r(I)} I {\displaystyle I}
证明 : " ⊇ {\displaystyle \supseteq } x ∈ V ( I ) {\displaystyle x\in V(I)} g ∈ r ( I ) {\displaystyle g\in r(I)} k ∈ N {\displaystyle k\in \mathbb {N} } g k ∈ I {\displaystyle g^{k}\in I} g k ( x ) = g ( x ) k = 0 {\displaystyle g^{k}(x)=g(x)^{k}=0} g ( x ) ≠ 0 {\displaystyle g(x)\neq 0} g ( x ) k ≠ 0 {\displaystyle g(x)^{k}\neq 0} x ∈ V ( r ( I ) ) {\displaystyle x\in V(r(I))} ◻ {\displaystyle \Box }
从微积分我们都知道 R n {\displaystyle \mathbb {R} ^{n}} R n {\displaystyle \mathbb {R} ^{n}} F {\displaystyle \mathbb {F} } F n {\displaystyle \mathbb {F} ^{n}} F n {\displaystyle \mathbb {F} ^{n}} Spec R {\displaystyle \operatorname {Spec} R} R {\displaystyle R} R = F [ x 1 , … , x n ] {\displaystyle R=\mathbb {F} [x_{1},\ldots ,x_{n}]} F n {\displaystyle \mathbb {F} ^{n}} Spec R {\displaystyle \operatorname {Spec} R}
引理 21.12 :
令 F {\displaystyle \mathbb {F} } R := F [ x 1 , … , x n ] {\displaystyle R:=\mathbb {F} [x_{1},\ldots ,x_{n}]} ( α 1 , … , α n ) ∈ F n {\displaystyle (\alpha _{1},\ldots ,\alpha _{n})\in \mathbb {F} ^{n}}
⟨ x 1 − α 1 , … , x n − α n ⟩ {\displaystyle \langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle } 是 R {\displaystyle R}
证明 :
设置
φ : F [ x 1 , … , x n ] → F , φ ( f ) := f ( α 1 , … , α n ) {\displaystyle \varphi :\mathbb {F} [x_{1},\ldots ,x_{n}]\to \mathbb {F} ,\varphi (f):=f(\alpha _{1},\ldots ,\alpha _{n})} 这是一个满射环同态。 我们声称它的核由 ⟨ x 1 − α 1 , … , x n − α n ⟩ {\displaystyle \langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle } ⟨ x 1 − α 1 , … , x n − α n ⟩ ⊆ ker φ {\displaystyle \langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle \subseteq \ker \varphi } 是 trivial 的。 我们现在将证明另一个方向,它不是 trivial 的。 对于给定的 f ∈ F [ x 1 , … , x n ] {\displaystyle f\in \mathbb {F} [x_{1},\ldots ,x_{n}]} f ~ ( x 1 , x 2 , … , x n ) := f ( x 1 + α 1 , … , x n + α n ) {\displaystyle {\tilde {f}}(x_{1},x_{2},\ldots ,x_{n}):=f(x_{1}+\alpha _{1},\ldots ,x_{n}+\alpha _{n})}
f ( x 1 , x 2 , … , x n ) = f ( x 1 + α 1 − α 1 , … , x n + α n − α n ) = f ~ ( x 1 − α 1 , x 2 − α 2 , … , x n − α n ) . {\displaystyle {\begin{aligned}f(x_{1},x_{2},\ldots ,x_{n})&=f(x_{1}+\alpha _{1}-\alpha _{1},\ldots ,x_{n}+\alpha _{n}-\alpha _{n})\\&={\tilde {f}}(x_{1}-\alpha _{1},x_{2}-\alpha _{2},\ldots ,x_{n}-\alpha _{n}).\end{aligned}}} 此外, f ( α 1 , … , α n ) = 0 {\displaystyle f(\alpha _{1},\ldots ,\alpha _{n})=0} f ~ ( 0 , … , 0 ) = 0 {\displaystyle {\tilde {f}}(0,\ldots ,0)=0} f ~ {\displaystyle {\tilde {f}}} f ~ {\displaystyle {\tilde {f}}} ⟨ x 1 , … , x n ⟩ {\displaystyle \langle x_{1},\ldots ,x_{n}\rangle } f ~ {\displaystyle {\tilde {f}}} F [ x 1 , … , x n ] {\displaystyle \mathbb {F} [x_{1},\ldots ,x_{n}]} x 1 , … , x n {\displaystyle x_{1},\ldots ,x_{n}} x j − α j {\displaystyle x_{j}-\alpha _{j}} x j {\displaystyle x_{j}}
因此,根据环同构第一定理,
F [ x 1 , … , x n ] / ⟨ x 1 − α 1 , … , x n − α n ⟩ ≅ F {\displaystyle \mathbb {F} [x_{1},\ldots ,x_{n}]{\big /}\langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle \cong \mathbb {F} } 因此, F [ x 1 , … , x n ] / ⟨ x 1 − α 1 , … , x n − α n ⟩ {\displaystyle \mathbb {F} [x_{1},\ldots ,x_{n}]{\big /}\langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle } ⟨ x 1 − α 1 , … , x n − α n ⟩ {\displaystyle \langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle } ◻ {\displaystyle \Box }
引理 21.13 :
令 F {\displaystyle \mathbb {F} }
M F := { ⟨ x 1 − α 1 , … , x n − α n ⟩ | ( α 1 , … , α n ) ∈ F n } {\displaystyle {\mathcal {M}}_{\mathbb {F} }:=\left\{\langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle {\big |}(\alpha _{1},\ldots ,\alpha _{n})\in \mathbb {F} ^{n}\right\}} (根据前面的引理,这是一个 Spec F [ x 1 , … , x n ] {\displaystyle \operatorname {Spec} \mathbb {F} [x_{1},\ldots ,x_{n}]}
Φ : F n → M F , f ( ( α 1 , … , α n ) ) := ⟨ x 1 − α 1 , … , x n − α n ⟩ {\displaystyle \Phi :\mathbb {F} ^{n}\to {\mathcal {M}}_{\mathbb {F} },f((\alpha _{1},\ldots ,\alpha _{n})):=\langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle } 是一个双射。
证明 :
该函数当然是满射的。令 ⟨ x 1 − α 1 , … , x n − α n ⟩ = ⟨ x 1 − β 1 , … , x n − β n ⟩ {\displaystyle \langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle =\langle x_{1}-\beta _{1},\ldots ,x_{n}-\beta _{n}\rangle } β j ≠ α j {\displaystyle \beta _{j}\neq \alpha _{j}} j ∈ { 1 , … , n } {\displaystyle j\in \{1,\ldots ,n\}} x j − β j ∈ ⟨ x 1 − α 1 , … , x n − α n ⟩ {\displaystyle x_{j}-\beta _{j}\in \langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle }
0 ≠ α j − β j = x j − β j − ( x j − α j ) ∈ ⟨ x 1 − α 1 , … , x n − α n ⟩ {\displaystyle 0\neq \alpha _{j}-\beta _{j}=x_{j}-\beta _{j}-(x_{j}-\alpha _{j})\in \langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle } 因此, ⟨ x 1 − α 1 , … , x n − α n ⟩ {\displaystyle \langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle } F [ x 1 , … , x n ] {\displaystyle \mathbb {F} [x_{1},\ldots ,x_{n}]} ◻ {\displaystyle \Box }
很容易验证这些集合 Φ − 1 ( O ) {\displaystyle \Phi ^{-1}(O)} O ⊆ M F {\displaystyle O\subseteq {\mathcal {M}}_{\mathbb {F} }}
有一种非常简单的方法来描述扎里斯基拓扑
定理 21.15 :
设 F {\displaystyle \mathbb {F} } F n {\displaystyle \mathbb {F} ^{n}}
证明 :
不幸的是,对于集合 T ⊆ F [ x 1 , … , x n ] {\displaystyle T\subseteq \mathbb {F} [x_{1},\ldots ,x_{n}]} V ( T ) {\displaystyle V(T)} T {\displaystyle T} F [ x 1 , … , x n ] {\displaystyle \mathbb {F} [x_{1},\ldots ,x_{n}]} p {\displaystyle p} T ⊆ p {\displaystyle T\subseteq p} V ~ ( T ) {\displaystyle {\tilde {V}}(T)}
设 A ⊆ F n {\displaystyle A\subseteq \mathbb {F} ^{n}} A = Φ − 1 ( V ~ ( T ) ∩ M F ) {\displaystyle A=\Phi ^{-1}({\tilde {V}}(T)\cap {\mathcal {M}}_{\mathbb {F} })} Φ {\displaystyle \Phi } T ⊆ R := F [ x 1 , … , x n ] {\displaystyle T\subseteq R:=\mathbb {F} [x_{1},\ldots ,x_{n}]} A = V ( T ) {\displaystyle A=V(T)} α ∈ F n {\displaystyle \alpha \in \mathbb {F} ^{n}}
α ∈ V ( T ) ⇔ ∀ f ∈ T : f ( α ) = 0 ⇔ ∀ f ∈ T : ( ( x 1 − α 1 ) | f ∨ ⋯ ∨ ( x 1 − α 1 ) | f ) ⇔ ∀ f ∈ T : f ∈ ⟨ x 1 − α 1 , … , x n − α n ⟩ ⇔ T ⊆ Φ ( α ) ⇔ Φ ( α ) ∈ V ~ ( T ) ⇔ α ∈ Φ − 1 ( V ~ ( T ) ∩ M F ) {\displaystyle {\begin{aligned}\alpha \in V(T)&\Leftrightarrow \forall f\in T:f(\alpha )=0\\&\Leftrightarrow \forall f\in T:\left((x_{1}-\alpha _{1})|f\vee \cdots \vee (x_{1}-\alpha _{1})|f\right)\\&\Leftrightarrow \forall f\in T:f\in \langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle \\&\Leftrightarrow T\subseteq \Phi (\alpha )\\&\Leftrightarrow \Phi (\alpha )\in {\tilde {V}}(T)\\&\Leftrightarrow \alpha \in \Phi ^{-1}({\tilde {V}}(T)\cap {\mathcal {M}}_{\mathbb {F} })\end{aligned}}} 现在令 V ( S ) {\displaystyle V(S)} V ( S ) = Φ − 1 ( V ~ ( S ) ∩ M F ) {\displaystyle V(S)=\Phi ^{-1}({\tilde {V}}(S)\cap {\mathcal {M}}_{\mathbb {F} })} S {\displaystyle S} T {\displaystyle T} ◻ {\displaystyle \Box }
事实上,我们可以用这种方式定义扎里斯基拓扑(即,仅仅定义 闭集为代数集),但这样就会隐藏我们已经知道的扎里斯基拓扑与它的联系。
我们现在将继续给出下一个重要的定义,它也解释了为什么我们处理不可约空间。
通常,我们将簇 简称为代数簇 。
我们有一个关于代数簇的简单刻画。但为了证明它,我们首先需要一个定义和定理。
证明 :
首先令 T {\displaystyle T} V ( T ) = V ( S ) {\displaystyle V(T)=V(S)} f ∈ T {\displaystyle f\in T} x ∈ V ( S ) = V ( T ) {\displaystyle x\in V(S)=V(T)} f ( x ) = 0 {\displaystyle f(x)=0} f ∈ I ( V ( S ) ) {\displaystyle f\in I(V(S))} T ⊆ I ( V ( S ) ) {\displaystyle T\subseteq I(V(S))}
因此, S ⊆ I ( V ( S ) ) {\displaystyle S\subseteq I(V(S))} V ( I ( V ( S ) ) ) ⊆ V ( S ) {\displaystyle V(I(V(S)))\subseteq V(S)} x ∈ V ( S ) {\displaystyle x\in V(S)} f ∈ I ( V ( S ) ) {\displaystyle f\in I(V(S))} f ( x ) = 0 {\displaystyle f(x)=0} x ∈ V ( I ( V ( S ) ) ) {\displaystyle x\in V(I(V(S)))} V ( S ) ⊆ V ( I ( V ( S ) ) ) {\displaystyle V(S)\subseteq V(I(V(S)))} ◻ {\displaystyle \Box }
证明 :
令第一个 p ≤ F [ x 1 , … , x n ] {\displaystyle p\leq \mathbb {F} [x_{1},\ldots ,x_{n}]} V ( p ) = V ( S ) ∪ V ( T ) {\displaystyle V(p)=V(S)\cup V(T)} V ( S ) , V ( T ) {\displaystyle V(S),V(T)} V ( p ) {\displaystyle V(p)} V ( p ) {\displaystyle V(p)} x ∈ V ( p ) ∖ V ( T ) {\displaystyle x\in V(p)\setminus V(T)} y ∈ V ( p ) ∖ V ( S ) {\displaystyle y\in V(p)\setminus V(S)} g ∈ T {\displaystyle g\in T} g ( x ) ≠ 0 {\displaystyle g(x)\neq 0} f ∈ S {\displaystyle f\in S} f ( y ) ≠ 0 {\displaystyle f(y)\neq 0} f ⋅ g ∈ p {\displaystyle f\cdot g\in p} z ∈ V ( S ) ∪ V ( T ) {\displaystyle z\in V(S)\cup V(T)} f ( z ) = 0 {\displaystyle f(z)=0} g ( z ) = 0 {\displaystyle g(z)=0} f ∈ p {\displaystyle f\in p} g ∈ p {\displaystyle g\in p}
Let now V ( S ) {\displaystyle V(S)} I := I ( V ( S ) ) {\displaystyle I:=I(V(S))} f g ∈ I {\displaystyle fg\in I} f ∈ I {\displaystyle f\in I} g ∈ I {\displaystyle g\in I} J f := I + ⟨ f ⟩ {\displaystyle J_{f}:=I+\langle f\rangle } J g := I + ⟨ g ⟩ {\displaystyle J_{g}:=I+\langle g\rangle } J f {\displaystyle J_{f}} J g {\displaystyle J_{g}} I {\displaystyle I} V ( J f ) ≠ V ( S ) {\displaystyle V(J_{f})\neq V(S)} V ( J g ) ≠ V ( S ) {\displaystyle V(J_{g})\neq V(S)} J f ⊆ I {\displaystyle J_{f}\subseteq I} J g ⊆ I {\displaystyle J_{g}\subseteq I} V ( J f ) {\displaystyle V(J_{f})} V ( J g ) {\displaystyle V(J_{g})} V ( S ) {\displaystyle V(S)} x ∈ V ( S ) = V ( I ) {\displaystyle x\in V(S)=V(I)} f g ( x ) = f ( x ) g ( x ) = 0 {\displaystyle fg(x)=f(x)g(x)=0} f ( x ) = 0 {\displaystyle f(x)=0} g ( x ) = 0 {\displaystyle g(x)=0} x ∈ J f {\displaystyle x\in J_{f}} x ∈ J g {\displaystyle x\in J_{g}} V ( S ) {\displaystyle V(S)}
V ( S ) = V ( J g ) ∪ V ( J f ) {\displaystyle V(S)=V(J_{g})\cup V(J_{f})} 并且不可约。因此,如果存在不可约性,则 I ( V ( S ) ) {\displaystyle I(V(S))} V ( I ( V ( S ) ) ) = V ( S ) {\displaystyle V(I(V(S)))=V(S)} ◻ {\displaystyle \Box }
定理 21.19 :
F n {\displaystyle \mathbb {F} ^{n}}
证明 :
令 O 1 ⊆ O 2 ⊆ ⋯ ⊆ O k ⊆ ⋯ {\displaystyle O_{1}\subseteq O_{2}\subseteq \cdots \subseteq O_{k}\subseteq \cdots } Φ {\displaystyle \Phi } M F {\displaystyle {\mathcal {M}}_{\mathbb {F} }} U j = Φ ( O j ) {\displaystyle U_{j}=\Phi (O_{j})} j ∈ N {\displaystyle j\in \mathbb {N} } Φ {\displaystyle \Phi }
U 1 ⊆ U 2 ⊆ ⋯ ⊆ U k ⊆ ⋯ {\displaystyle U_{1}\subseteq U_{2}\subseteq \cdots \subseteq U_{k}\subseteq \cdots } 由于 F {\displaystyle \mathbb {F} } F [ x 1 , … , x n ] {\displaystyle \mathbb {F} [x_{1},\ldots ,x_{n}]} U j {\displaystyle U_{j}} N ∈ N {\displaystyle N\in \mathbb {N} } Φ {\displaystyle \Phi } O j = Φ − 1 ( Φ ( O j ) ) = Φ − 1 ( U j ) {\displaystyle O_{j}=\Phi ^{-1}(\Phi (O_{j}))=\Phi ^{-1}(U_{j})} O j {\displaystyle O_{j}} N {\displaystyle N} ◻ {\displaystyle \Box }
推论 21.20 :
每个代数集 V ( S ) {\displaystyle V(S)}
V ( S ) = V ( p 1 ) ∪ V ( p 2 ) ∪ ⋯ ∪ V ( p k ) {\displaystyle V(S)=V(p_{1})\cup V(p_{2})\cup \cdots \cup V(p_{k})} 对于某些素理想 p 1 , … , p n ≤ F [ x 1 , … , x n ] {\displaystyle p_{1},\ldots ,p_{n}\leq \mathbb {F} [x_{1},\ldots ,x_{n}]} V ( p j ) {\displaystyle V(p_{j})}
也就是说,我们可以将代数集分解成代数簇。
证明 :
结合定理 21.19、21.7 和 21.18。 ◻ {\displaystyle \Box }
练习 21.2.1 :设 f , g ∈ F [ x 1 , … , x n ] {\displaystyle f,g\in \mathbb {F} [x_{1},\ldots ,x_{n}]} V ( { f ⋅ g } ) = V ( { f } ) ∪ V ( { g } ) {\displaystyle V(\{f\cdot g\})=V(\{f\})\cup V(\{g\})} 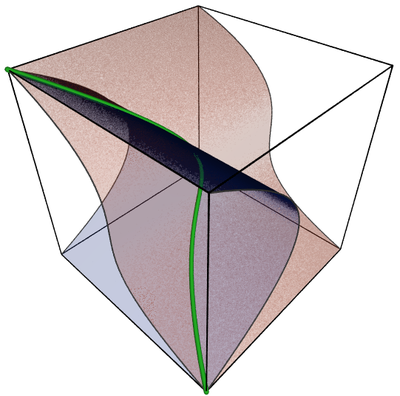












































































































![{\displaystyle S\subseteq \mathbb {F} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d23cfd8daa9c6aa4c7b04b3c5c69db8a4218f40)

![{\displaystyle f\in \mathbb {F} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afe87b11d04d0b531a4519e5c3a8bf262acd59da)








![{\displaystyle R:=\mathbb {F} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/404e94398eaa74b6c5ee5c55baa61c8c535d2ef1)
































![{\displaystyle I\subseteq \mathbb {F} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6efb364a62947acb7f82fa1d7a59e6495e65317e)












![{\displaystyle R=\mathbb {F} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d29adb69cc5d8c8d76f502568c105cb5e45d1903)


![{\displaystyle \varphi :\mathbb {F} [x_{1},\ldots ,x_{n}]\to \mathbb {F} ,\varphi (f):=f(\alpha _{1},\ldots ,\alpha _{n})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a06d5a7cf188e85ef6b6cbbfaead8a00135f3c2f)







![{\displaystyle \mathbb {F} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/096a47b8d74b985081288a6194e5035494194845)



![{\displaystyle \mathbb {F} [x_{1},\ldots ,x_{n}]{\big /}\langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle \cong \mathbb {F} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1af89ed2e29d9dabf315b39557070d4178781fe7)
![{\displaystyle \mathbb {F} [x_{1},\ldots ,x_{n}]{\big /}\langle x_{1}-\alpha _{1},\ldots ,x_{n}-\alpha _{n}\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cec032cef75d52e67aefba0e24e28822318b438)

![{\displaystyle \operatorname {Spec} \mathbb {F} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b381e202bcf969a18b28a484ee7f66e81b056f6)











![{\displaystyle T\subseteq \mathbb {F} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8315ee9f7c822f5a6f8dfd37395ab49cfd5bf551)






![{\displaystyle T\subseteq R:=\mathbb {F} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f745c5cb65da8ec1b4619f4fc97648baf6d62b3)





![{\displaystyle I(V(S)):=\{f\in \mathbb {F} [x_{1},\ldots ,x_{n}]|\forall x\in V(S):f(x)=0\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b7138825c6d395b815181a93ef5025bc392b55f)













![{\displaystyle p\leq \mathbb {F} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/764720142edaaf05184ce3fd216dc2ee1e2d4ebb)













































![{\displaystyle p_{1},\ldots ,p_{n}\leq \mathbb {F} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/436c82ca2bda7048c5b9cb82a64179731cb14185)

![{\displaystyle f,g\in \mathbb {F} [x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3d405c1ad77f9e7e8b93a48afeb254abec35ec7)
