计算机系统工程/马尔可夫模型
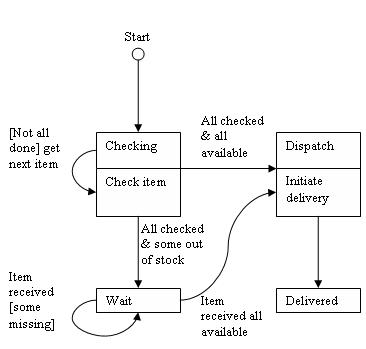
状态图描述了系统的行为。它们描述了系统的所有可能状态(UML 中的对象)以及状态如何随着到达系统的事件(对象)而改变。
例如:
需要注意的是,马尔可夫模型将状态转换视为一个随机过程。
假设每个状态由一个随机变量定义。随机变量集 {xn} 构成一个马尔可夫链,如果下一个值(状态)为 xn+1 的概率仅取决于当前值(状态)xn,而与任何先前值无关。整个先前历史对未来行为的影响都总结在当前状态中。对于“离散时间”马尔可夫链,转换只能在整数 1、2、3 … 发生。对于“连续时间”马尔可夫链,转换可以在任何时间发生。这很重要,因为过去的历史完全由当前状态指定,我们也不能指定进程在当前状态中停留了多长时间。
分析:P(x(tn+1) = xn+1 | x(tn) = xn, x(tn-1) = xn-1, … x(t1) = x1) = P(x(tn+1) = xn+1 | x(tn) = xn),其中 t1 < t2 < … < tn < tn+1 且 x1、x2、…、xn 处于某个离散状态空间中。
考虑离散时间马尔可夫链
观察:离开每个城市的概率之和为 1。
P(xn = j | x1 = i1, x2 = i2, …, xn-1 = in-1) = P(xn = j | xn-1 = in-1)。
P(xn = j | xn-1 = in-1) 是一个一步转移概率。该概率从一步 n-1 的状态 E=i 转移到一步 n 的状态 E=j。
令 Pij(n) = 系统在 n-1 步内从状态 Ei 转移到状态 Ej 的概率。然后,是系统在一步内从状态 Ei 转移到状态 Ek,然后在 n-1 步内从状态 Ek 转移到状态 Ej 的概率。这称为查普曼-科尔莫哥洛夫方程。
令 P(n) 为矩阵。每个条目都是 Pij(n)。如果这是一个 n 步转移概率矩阵,那么
(如果与 n 无关,则称为齐次)
定义 Pij = P(xn = j | xn-1 = i) 作为系统在状态 Ei 时转移到下一个状态 Ej 的概率。这称为一步转移概率集。
示例:P00 = 0,P01 = ¾,P02 = ¼,P12 = ¾
以矩阵形式
令 πj = P(xn = j) 为系统在步 n 时处于状态 j 的概率。在我们的示例中,
步 n+1 时处于状态 j 的概率是在步 n 时处于状态 i 并在一步内转移到状态 j 的概率。
以向量形式
特别地,
例如:令 Π(0) = [0,1,0],从哥伦比亚开始。
经过很长时间后,令
因此,
示例
观察
(1) 和 (2) 之和为负 (3),因此方程之间存在线性相关性,因此没有唯一解。我们还知道 π0 + π1 + π2 = 1(即系统必须处于某个状态)。这称为归一化条件。
现在求解
观察
这就像掷硬币,其中 r = 正面概率,1-r = 反面概率。因此,P(正好有 m 个正面的序列) = rm (1-r)。
假设该进程进入状态 Ei。然后,在下一步中停留在状态 Ei 的概率是 Pii。进程在下一步中离开 Ei 的概率是 1-Pii。每一步都是独立的,所以 P(系统在刚进入状态 Ei 后正好再停留 m 步) = (1-Pii) Piim。换句话说,该进程以 m*( Pii Pii Pii …Pii) 的概率停留 m 步,并在第 m+1 步离开状态。
状态 Ei 中的平均时间是 E(在状态 E 中的时间)
现在,, 因此
因此,
简而言之,进程在离开状态之前停留的平均时间是离开概率的倒数。
假设观察状态 i k 步,并且该系统没有改变状态。进程在下一步中不离开状态的概率是多少?令 y = 到第一次离开的步数。
因此,该进程是无记忆的——正如我们所知。
P(x(tn+1) = j | x(tn) = in … x(t0) = i0) = P(x(tn+1) = j | x(tn) = in)
回想一下,马尔可夫链是无记忆的,因此转换不取决于进程在给定状态中停留的时间。
令 τi = 在状态 i 中停留的时间。P(τi > s+t | τi > s) = h(t),它只是 t 的函数(不是 s)。该函数显示了进程在状态中停留的时间。
因此,指数是唯一满足此条件的连续分布。同样,如果我们设置 s、t = 0,那么 P(τi >0) = 1,并且
现在,考虑时间 s ≤ u ≤ t。为了从时间 s 的状态 Ei 转移到时间 t 的状态 Ej,进程必须在时间 u 时经过某个状态。因此,
这是查普曼-科尔莫哥洛夫方程,与离散情况完全类似,但难以直接使用。
回想一下
在查普曼-科尔莫哥洛夫方程中,将 t+h 代入 t
除以 h,取 h 趋近于 0,u 趋近于 t 的极限
这称为科尔莫哥洛夫的前向方程。
此外,
是科尔莫哥洛夫的后向方程。
如果时间齐次转移概率不依赖于初始时间 t,而只依赖于间隔 h,则 qij(t) = qij 且 qj(t) = qj 且 = Pij(h),那么
状态转移概率和初始分布决定了马尔可夫链的所有属性。观察
除以 h,取 h 趋近于 0,v 趋近于 t 的极限
.
如果时间齐次
回想一下
如果系统有正概率不会返回到该状态,则该状态是瞬态状态。令 Xji = 从状态 j 开始访问状态 i 的次数。Xji 的期望值 E(Xji) 为
如果 E(Xji) 是有限的,则状态 i 是瞬态状态。这意味着 Pji(n) 在 n 趋近于无穷大时趋近于 0。
如果从状态 j 出发,一个过程以 1 的概率返回到状态 i,那么状态 i 就是循环状态。此外,它是无限的。
考虑从状态 j 到达状态 i 所需的时间,对于一个循环链。令 fij(n) = 在 n 步内从 i 首次访问 j 的概率。令 fii(n) = 在 n 步内从 i 首次返回 i 的概率。那么,从状态 i 出发访问 j 的概率为
如果 fii = 1,则状态 i 是循环状态,如果 fii < 1,则状态 i 是瞬态状态。如果 fii = 1,那么平均循环时间为。如果 是有限的,则状态称为非零循环状态,如果 是无限的,则状态称为零循环状态。
对于循环状态 i,状态 i 的周期 是使得 为正整数的集合 n 的最大公约数。如果 = 1,则系统是无周期的,如果 > 1,则系统是有周期的。
当且仅当 Pii = 1 时,系统是吸收的。
如果每个状态都可以在有限步内从其他任何状态到达,那么马尔可夫链是不可约的。不可约马尔可夫链的所有状态都是相同类型的。在一个无周期马尔可夫链中,所有状态都是无周期的。如果一个状态具有周期 d,那么所有状态都具有相同的周期 d。
连续时间马尔可夫链
[edit | edit source]令 = 随机变量 = 在状态 i 中的时间。马尔可夫性质意味着过渡的概率不能依赖于系统在一个状态中停留的时间。
现在对于 s=0,我们有
s = t = 0 再次需要
现在,
因此,在状态 i 中的时间呈指数分布,参数为,它可能取决于状态。
我们已经看到 = 在状态 i 中的时间,并且令 t 是时间 h 的一个很小的增量
最后一个等式是系统在下一个时间增量 h 内离开状态的概率。这可以用泰勒级数表示
将状态编号为 0,1…,令 = 过渡到更高编号状态(出生)的概率。令 = 过渡到较低编号状态(死亡)的概率。只允许过渡到下一个更高或更低编号状态(或停留在相同状态)。这被称为生死过程。
令 P(n=k,t) = 在时间 t 处于状态 k 的概率。考虑一个过程如何在时间 t+h 进入状态 n=k。
对于出生:必须处于状态 n=k-1,并且发生出生事件。
对于死亡:必须处于状态 n=k+1,并且发生死亡事件。
如果没有出生和死亡:必须在时间 t 处于状态 n=k。
平衡方程
[edit | edit source]平衡平衡方程
[edit | edit source]流量平衡
[edit | edit source]平衡平衡方程可以通过下面所示的状态转换速率图直观地推导出来。
这类似于我们已经见过的状态转换图。在平衡状态下,进入一个状态的概率流率必须等于从该状态流出的概率流率。因此
求解平衡方程
[edit | edit source]数量 称为“交通强度”,通常用 表示。
回想一下,如果作业到达的速度快于处理的速度,队列将不稳定。因此
正如我们将看到的,决定了队列中大多数感兴趣的属性。请注意,它是通过到达率和服务率的比率来确定的,而不是它们的绝对值。具有相同交通强度的队列可以预期具有相似的属性,即使它们的到达率或服务率可能大不相同。
常数 P(0) 是使用归一化要求确定的,如下所示
请注意最后一个方程与几何分布的相似性
这是队列中有 k 个作业的概率,如下所示
队列中至少有 1 个作业的概率为。这是服务器的利用率,即服务器繁忙的概率。
队列中的数量
[edit | edit source]队列中作业的平均数量为
求和是使用以下技巧进行评估的:注意
现在由于导数的和是和的导数,
这在 从 0 增加到 1 时显示如下
队列中作业数量超过 r 的概率为
这在几个 值时显示如下
请注意,P(n≥r) 在 中呈几何下降。还要记住, 是服务器的利用率。因此,对于利用率低的服务器( 较小),队列中存在大量作业的可能性很小。对于利用率高的服务器( 接近 1),等待服务的作业数量多的可能性要高得多。
令 T = 平均等待时间,Tn = 抵达 n 的等待时间,系统中有 n-1 个客户,xi = 第 i 个客户的服务需求(i = 1,2,…,n),xo = 正在服务的客户的剩余服务时间,以及 xn = 第 n+1 个客户的服务需求。