计算机系统工程/概率
一个实验,真实的或想象的,可以用三个特性来描述。这些是
- 1. 一组结果
- 2. 将这些结果分组为类别
- 3. 这些类别出现的相对频率。
例如,抛硬币是一个实验,其结果要么是正面要么是反面。一组结果将是正面 (H) 或反面 (T)。那么正面的相对频率将是在大量抛掷中正面出现的次数。
(1)
如果将成对的抛掷作为实验的结果,则结果集将是 HH、HT、TH 和 TT。这些可以分为三类:2 个正面、2 个反面和 1 个正面和 1 个反面。假设硬币是公平的,则 1 个正面和 1 个反面的类别的相对频率将是其他两类的两倍。
在概率论中,“样本空间”,用 S 表示,对应于结果集,每个可能的结果都是 S 的一个元素。“事件”对应于一类结果,“概率”是事件相对频率的度量。这可以解释为如果实验重复多次,事件发生的次数占总次数的比例。
(2)
形式上,概率测度满足以下性质
*1. For any event A, 0≤P(A)≤1 *2. P(S) = 1 *3. If A and B are mutually exclusive events then P(A+B)=P(A)+P(B). (3)
A + B 是样本空间中包含事件 A 或 B 或两者都包含的元素的集合。事件 A 可以描述为
A = {ω: ω satisfies membership property for A} (4)
其中 ω 是样本空间的成员,ωєS。这读作:“A 是 ω 的集合,其中 ω 满足 A 的成员属性。”类似地,引入集合论符号表示事件的补集、并集和交集,令
AC = {ω: ω not in A}
= complement of A
A + B = {ω: ω in A or B or both}
= union of A and B* (5)
A,B = {ω: ω in both A and B}
= intersection of A and B*
Ø = SC = null event = no sample points since all sample points are in S
- 在集合论符号中,“+”和“U”都用于表示两个集合的并集。类似地,交集用“,”、“∩”、“∙”表示,或者有时通过将符号并排写来表示。“+”和“∙”暗示了加法和乘法的算术运算,集合的并集和交集运算与此类似。但是,不应该将它们混淆。一个应用于集合,另一个应用于数字。
这些在下图的韦恩图中进行了说明。正方形中的点表示样本空间 S,封闭循环中的点表示事件。
在 I 中注意
S = A + AC (6)
并且 AC 和 A 中的点是互斥的。因此,使用 (3)
P(S)= P(AC + A) (7)
= P(AC)+P(A)
但 P(S) = 1,因此
P(AC) = 1 - P(A) (8)
在 IV 中,A 和 B 中的点不是互斥的。在这种情况下
(9)
(9) 中的最后一项是必要的,因为前两项都包含 A、B 中的点,但我们只想在 A+B 中计算这些点一次。
条件概率
如果事件 B 发生,“条件概率”A 也发生的概率 P(A|B)(读作:“给定 B 时 A 的概率”)定义为
(10)
这给出了 B 中也属于 A 的点的分数。实际上,有了 B 的知识,我们可以创建一个新的样本空间,其中仅包含 B 中的点,然后查找 A 中属于 B 的点的相对频率。
如果
P(A,B) = P(A) P(B) (11)
则称 A 和 B 是独立的。
(12)
注意,如果 A 和 B 是独立的,则
A + AC = S (13) A, AC = Ø
这意味着 B 的知识不会告诉我们 A 发生的频率。正如我们在 (5) 和 (6) 中提到的,A 和 AC 覆盖 S 并且是互斥的。
B = B,A + B, AC (14)
因此
P(B) = P(B,A + B, AC) (15) = P(B,A) + P(B, AC)
由 (10)
P(B,A) = P(B|A) P(A) (16)
和
P(B,AC) = P(B|AC) P(AC) (17)
因此
P(B) = P(B|A) P(A) + P(B|AC) P(AC) (18)
如果事件 Ai,i = 1,2…n 是互斥且穷举的,即
A1 + A2 +… An = S (19) Ai,Aj = Ø for all i ≠ j
则 (15) 和 (18) 可以更一般地写成
(20)
和
(21)
这就是“全概率公式”。另一个有用的关系来自 (10),即“贝叶斯定理”
(22)
然而,由 (18)
P(B) = P(B|A)P(A) + P(B|AC)P(AC) (23)
因此
(24)
因此,如果我们知道事件 A 的概率 P(A) 和 A 对 B 的概率的影响 P(B|A),则可以计算 B 对 A 的概率的影响 P(A|B)。
一个例子
贝叶斯定理在组件测试中可能有一些非直观的结论。
假设我们有一种测试内存芯片的方法。如果芯片损坏 (B),则测试 95% 的时间会显示损坏 (T)。
P(T|B) = .95 (25)
如果芯片完好 (BC),则测试 95% 的时间会显示完好 (TC)。
P(TC|BC) = .95 (26)
另外,假设 1% 的芯片损坏。
P(B) = .01 (27)
测试结果为损坏的芯片中,有多少百分比是真正损坏的?即,P(B|T) 是多少?应用 (24) 我们有
(28)
由 (8)
P(BC) = 1 – P(B) = .99 P(T| BC) = 1 – P(TC|BC) = .05 (29)
这意味着 B 的知识不会告诉我们 A 发生的频率。正如我们在 (5) 和 (6) 中提到的,A 和 AC 覆盖 S 并且是互斥的。
(30)
此外,测试结果为完好的芯片中,完好芯片的概率为
(31)
并且由 (8)
P(TC|B) = 1 - P(T|B) = .05 (32)
这意味着 B 的知识不会告诉我们 A 发生的频率。正如我们在 (5) 和 (6) 中提到的,A 和 AC 覆盖 S 并且是互斥的。
(33)
因此,几乎所有测试结果为完好的芯片都是完好的,但只有 16% 测试结果为损坏的芯片确实有缺陷。该测试并没有我们希望的那样有辨识力。
组合和排列
N 个可区分的对象可以以 N! 种不同的方式排序(排列)。这很容易通过观察得出,任何 N 个对象都可以放在第一个位置;其余 n-1 个对象中的任何一个都可以放在第二个位置;依此类推,直到只有一个对象可以放在最后一个位置。
更一般地,可以从 N 个对象的集合中选择 r 个对象的集合,有 N(N—1) (N—2) ... (N—r+1) = N! / (N—r)! 种不同的方式。这是不放回抽样。如果 r =N,则有 N! 个集合,每个集合仅仅是 N 个对象的排序。
一旦选择,集合中的 r 个对象可以在不改变集合组成的情况下以 r! 种不同的方式排序。每个排序对应于 N! / (N—r)! 抽样中的另一个抽样。因此,如果只考虑所选对象而不考虑它们的顺序,则有
种不同的方式从 N 个对象的集合中选择 r 个对象。这称为从 N 个对象中取 r 个对象的组合,并使用特殊的符号表示
注意,对于 r = N,
以及对于 r = 1,
组合也可以被认为是将对象划分为分别包含 r 个对象和 (N—r) 个对象的组的方式的数量。这自然地导致了 N 个对象可以被划分为 k 个组,第 i 个组包含 ni 个对象,i = 1,2,…k 且 N = Σni 的扩展
种不同的方式。
随机变量是一个变量,其值取决于实验的结果。因此,随机变量实际上是一个函数,它将数值分配给样本空间 S 中的每个事件。在实践中,随机变量分配给事件的值被选择为具有某种物理意义。例如,如果我们对抛硬币实验下注,正面赢 1.00 美元,反面输 0.50 美元,则随机变量 X 可以分配以下值
(34)
其中 ω 是实验的结果。
通常,我们感兴趣的是随机变量取特定值的概率。
P(X = x) (35)
这是样本空间的成员 ω(其中 X(ω) = x)出现的相对频率之和。也就是说
P(X = x) = relative frequency for which X(ω) = x. (36)
如果硬币是公平的(即正面和反面出现的可能性相同)在 (34) 中,则
P(X = 1) = 1/2 P(X = -.5) = 1/2 (37)
概率的另一种有用表示是“概率分布函数”,
(38)
这也称为“累积分布函数”。它在 (34) 中显示如下
注意,由于 S 中的每个点都由随机变量映射到实数线上
P ( X ≤ -∞ ) = 0 P ( X ≤ ∞ ) = 1 P ( X ≤ x ) ≥ 0, for all x on the real line (39)
此外,对于实数线上的两个点 a 和 b
P ( X ≤ b) – P (X ≤ a ) = P ( a < X ≤ b ), for a < b (40)
和
P ( X ≤ b) ≥ P (X ≤ a ), for a ≤ b (41)
用于描述抛硬币实验的随机变量只能取有限数量的值(在这种情况下为 2:+1 和 -0.5)。这称为离散随机变量。用于描述其他实验(例如,两件事发生之间的时间)的随机变量可能更适当地具有连续的值范围。这种“连续随机变量”具有连续分布函数,我们用以下表示
F ( x ) = P ( X ≤ x ) (42)
与离散情况一样,F(x) 是一个非递减函数,并且
0 ≤ F(x) ≤ 1 , for all x. (43)
这种随机变量的一个常见例子是指数分布的随机变量
(44)
其中 λ < 0。这在下图中显示
出于计算目的,另一个函数“概率密度函数”通常比分布函数更方便。假设导数存在,则将其定义为分布函数的导数。
(45)
由于 F(x) 是非递减的,因此 f(x) ≥ 0。此外,由 (45)
(46)
和
1 = F(∞) = (47)
和
P ( a ≤ x ≤ b ) = F ( b ) – F ( a ) = (48)
因此,f ( x ) 是一个函数,当在其区间上积分时,给出随机变量 X 落在该区间内的概率。
注意,由 (47) 定义的 f ( x ) 曲线下的面积为 1。因此,令 Δx 为一个小区间
f ( x ) Δx
是一个高为 f ( x )、宽为 Δx 的矩形。然后 f ( x ) Δx 近似于 f ( x ) 曲线在 x 到 x + Δx 范围内曲线下的面积。
当 Δx 变为零时(用 dx 表示:lim Δx 0 Δx = dx),该近似值变得精确。因此,通常将 f ( x ) dx 视为 X“等于”x 的概率是有用的。
f(x)dx = P(X ‘=’ x) (49)
严格来说,它是 X 落在点 x 周围的一个非常小的区间内的概率。
在对计算机系统进行建模时,我们通常对系统中的作业数量、等待时间和服务需求等事物感兴趣,这些事物只能取非负值。用于描述这些量的随机变量只能取非负值
F(x) = P(X ≤ x) = 0, for x < 0 (50)
这通常使处理它们的数学运算稍微简单一些。在下文中,我们将假设随机变量是非负的,但这可以很容易地扩展到更一般的情况。
指数分布的随机变量 (44) 是一个非负随机变量。对于 x ≥ 0,它的导数在任何地方都定义为
= λe-λx (51)
期望值
尽管概率分布函数描述了大量实验的综合行为,但它通常过于复杂,无法用于比较替代实验的结果。我们需要一个单一的数字,“品质因数”,来表示实验的结果。这由随机变量的“期望值”、“平均值”或“均值”(这三个术语是同义词)提供。如果 X 是一个随机变量,则符号 E(X) 和
都用于表示其期望值。它被定义为随机变量的值与其实验给出此结果的频率的乘积之和。对于离散情况,这是
(52)
在连续情况下
(53)
在随机变量取整数值的重要情况下,(52) 变为
(54)
注意,这可以改写为
(55)
每列中各项的总和为 kP(N = k),其中 k = 1, 2, … 是列。但(55)的第一行只是 N > 0 的概率,第二行是 N > 1 的概率,依此类推。因此,我们也可以写成
(56)
根据分布函数 (38),我们有
P ( N > k ) = 1 – P ( N ≤ k ) (57)
给出
(58)
由于分布函数 P ( N ≤ k ) 通常比密度 P ( N = k ) 更容易测量或估计,因此 (58) 提供了一种计算随机变量平均值的便捷方法。
类似的结果在连续情况下也成立
(59)
这很容易通过分部积分 (59) 来证明
(60)
回想一下 F ( ∞ ) = 1 并且
(61)
这简化为
(62)
由于每个随机变量都与一个数字相关联,因此可以对其进行数值运算(加、乘等),并且可以像普通数字一样在其上定义任意函数。令 g(X) 是定义在随机变量 X 上的函数。期望值的定义 (52, 53) 可以扩展到给出 g(X) 的期望值:E(g(X))
E(g(X)) = (63)
如果 X 是离散的,或者
E(g(X)) = (64)
在连续情况下。
两个随机变量 X 和 Y 的和的期望值为
E ( X + Y ) = (65)
使用 (16),我们注意到
P ( X=x, Y=y ) = P ( X=x / Y=y ) P ( Y=y ) (66)
以及
P (X=x, Y=y ) = P ( Y=y, X=x ) = P (Y=y / X=x ) P ( X=x ) (67)
因此
E ( X + Y ) = (68)
现在
(69a)
和
(69b)
因此
E ( X+Y ) = E ( X ) + E ( Y ) (70)
此外,如果 X 和 Y 是独立的
E( X,Y ) = (71)
因为 X 和 Y 是独立的。因此
E ( X,Y ) = = E ( X ) E ( Y ) (72)
结果 (70 和 72) 也适用于 X 和 Y 是连续随机变量的情况。
回想一下 (21),
P (X=xi) = (73)
根据定义 (52)
E(X) = (74)
因此
E (X) = (75)
根据 (52) 的类比,(75) 中的第二个和被定义为给定 Y=yj 时 X 的条件期望值。这通常写成 E(X/Y)
E(X/Y) = E(X/ Y=yj) = (76)
因此 (75) 为
E(X) = (77)
但这只是 E(X/Y) 的期望值。
因此
E(X) = E( E(X/Y) ) (78)
同样,如果 X 是连续随机变量,这也适用。
方差
如前所述,密度函数下的面积为 1。如果将此“面积”剪下并放在一个支点上,则期望值是它将平衡的点。
由于与力学的关系,期望值通常称为随机变量的**一阶矩**。
另一个用于描述随机变量的有用品质因数是其“二阶矩”,定义为
E (X2) = (79)
对于离散情况,以及
E (X2) = (80)
对于连续情况。请注意,它是随机变量平方的期望值。
我们通常不直接使用二阶矩,而是更感兴趣的是找到“关于均值的二阶矩”或“二阶中心矩”。对于离散情况,这是
(81)
回想一下,第一个和是二阶矩 (79),第二个是均值 (52),第三个根据定义 (3) 必须为 1,这变成了
(82)
类似地,对于连续情况
(83)
二阶中心矩提供了随机变量的值围绕均值聚集的紧密程度的度量。例如,如果随机变量只能取一个值 α,则
P(X=x) = 1 for x= α (84) 0 for x≠ α
和
(85)
和
(86)
由此可见,根据 (82),
(87)
对于前面提到的指数分布随机变量 (44, 51)
(88)
和
(89)
因此
(90)
二阶中心矩实际上说明了随机变量中存在多少变化。恰如其分地,它通常被称为随机变量的“方差”,Var(X),并用符号 σ2 表示
(91)
请注意,由于 σ2 是随机变量平方的期望值,因此它始终为正。
此外,随机变量的标准差,用符号 σ 表示,定义为方差的平方根
(92)
请注意,这与随机变量和均值具有相同的度量单位。
尽管方差和标准差提供了对随机变量值中预期变化量的度量,但如果随机变量具有较大的均值,则给定数量的变化通常不如它较小时重要。“变异系数”C 提供了一种表达变化量与随机变量均值的关系的方法。它被定义为
(93)
请注意,对于确定性随机变量 (84, 87),σ = σ2 = 0,因此
C = 0 (94)
对于指数随机变量 (44, 90)
(95)
因此,在 (93) 中使用 (88) 和 (89)
(96)
三阶中心矩
三阶中心矩 M3 定义为
和
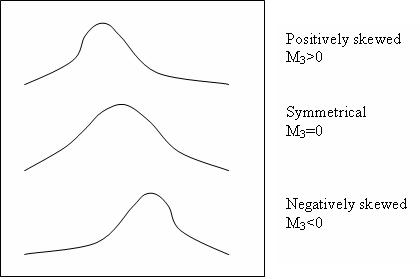
分别用于离散和连续情况。这提供了分布对称性的度量。
对于 M3 = 0,分布是对称的。对于 M3 > 0,它是正偏的,对于 M3 < 0,它是负偏的。如下所示。
四阶中心矩
四阶中心矩 M4 定义为
和
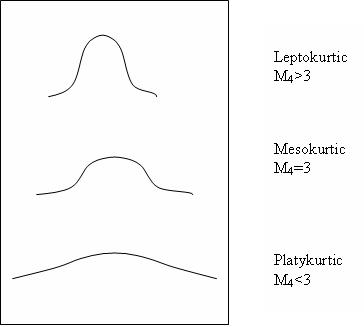
分别用于离散和连续情况,测量分布的平坦度或峰值。它是比方差更灵敏的分布扩展度量。
下图显示了具有相同方差 σ2 = 1 和 M4 > 3、M4 = 3 和 M4 < 3 的分布。对于 M4 > 3,分布是“高而瘦的”;对于 M4 < 3,它是“平的”,对于 M4 = 3,它是“中等”。
参考文献
- 1. Kleinrock,Leonard,排队系统卷 1:理论。John Wiley,纽约,1975 年。