计算机系统工程/排队系统模型
队列正式定义为由一个服务器和一个等待线组成,用于为需要服务于服务器的客户提供服务。每个客户都加入等待线的末尾。当等待线最前面的客户得到服务时,他们后面的客户会逐渐移动到等待线的最前面。客户一旦从服务器那里获得所需的服务,就会离开,服务器开始为等待线中的下一个客户提供服务。如下图所示。
许多自然系统都可以用这种方式来描述。例如,在一家杂货店里,购物者排队等候收银员结账。这里,购物者是顾客,收银员是服务器,而收银员为每个购物者结账所花费的时间是该购物者的服务需求。同样,在银行里,顾客排队等候出纳员,他们完成自己的交易。在这种情况下,所有出纳员都可以使用单一等待线。在计算机系统中,顾客是提交用于处理的任务,服务器是 CPU 或磁盘控制器等设备,而服务需求是任务在该设备上花费的时间。例如,如果服务器是 CPU,则服务需求是任务将获得的处理量;如果服务器是磁盘控制器,则服务需求是执行磁盘读或写操作的时间。
任务加入等待线并进入队列之间的时间以及每个任务所需的处理时间都是由随机变量给出的。到达率是每秒到达任务的平均数量。这用 λ 表示,因此 λ 是到达之间平均时间。
and are both used to represent the average service requirement. In a large interval T the expected number of arrivals is
在 T 时间内的预期到达数量 =
这些任务的平均服务需求为 μ。因此,服务器提供的预期服务量为
服务器繁忙的时间比例是它的利用率。这是
量 ρ 被称为队列的“交通强度”,用特殊符号 ρ 表示
注意,如果 ρ 大于 1,则到达的任务比在 T 时间内可以处理的任务多。在这种情况下,等待线中任务的数量会无限增长,队列不稳定。只有当到达过程和服务需求是确定性的时,队列才是稳定的。由于任务到达和/或服务需求的波动,非确定性队列必须有 ρ < 1 才能保持稳定。对于 ρ < 1,ρ 是服务器繁忙的概率(即时间比例)。因此,1 - ρ 是它空闲的概率。
在研究队列时,最重要的是要问以下问题
• How long must a job wait before receiving service? • How long will it stay in the queue before leaving (waiting time plus service time)? • How many jobs are in the queue? • What is the utilization of the server? (i.e. What fraction of the time is the server busy?)
在有限人口模型中,有固定数量 N 个任务。任务从某个来源到达队列,并在完成服务需求后返回到该来源。如下图所示
如果队列中有 k 个任务,则来源中有 N-k 个任务。我们假设任务在来源中等待呈指数分布的时间,平均时间为 θ,然后返回到队列,并且彼此独立。如果来源中有 (N-k) 个任务,那么它们会创建一个泊松输入过程到队列,速率为
有限人口 M/M/1 队列的状态转移图如下所示。
请注意,当队列中有 N 个任务时,来源中没有任务,λN = 0。因此,队列状态 n > N 的概率为零。
归一化方程变为
因此
或
它描述了平均排队长度、平均到达率和平均排队等待时间之间的关系。这个定理对于任何处于稳态条件的排队系统都适用。
一个客户在系统中花费时间 w,在此期间,客户以稳定的速度到达。这必须是系统中客户的平均数量(否则数量要么增加要么减少)。
形式上,
在具有不同类型客户的系统中,Little 公式分别适用于每种类型。例如,在优先级系统中,
考虑仅包含服务器的系统
Comten 网络处理器 数据包:2048B = 16,384 位 线路:56Kbps
292.5ms = .2924 秒 ≈ .3 秒
假设我们想每秒发送 7 个数据包的总量
但是,请记住,在 100% 利用率下存在延迟,
因此,我们可能实际上想使用 4 条线路来进一步降低利用率。
任务在队列中花费的平均时间可以通过 Little 公式求得
这称为队列的“响应时间”,用 T 表示。因此,使用 Wq = T - 1/μ,我们得到
或
如下图所示,随着 ρ 从 0 增加到 1,响应时间(和系统中的数量)也随之增加。
请注意,响应时间(和系统中的数量)在服务器利用率小于 50%(即 ρ < 0.5)时保持相当平稳,并且当服务器接近 100% 利用率时急剧上升。这种现象是几乎所有排队系统的特征。当我们试图让服务器接近其容量(即 ρ 接近 1)时,响应时间和队列中的数量会变得非常大。对于 ρ > 1,系统变得不稳定,队列中的数量和响应时间会无限增长。
停等协议会占用传输线路,因为线路上的时间用于发送数据包,然后会延迟,直到收到确认。
线路 = 服务器等待线路 = 要在站点的消息发送服务时间 = 传输时间
或者,使用停止并等待,服务时间 = 周期时间。
为了提高线路速度,必须缩短服务时间。
如果超过 m 个服务器繁忙,m 个服务器会拒绝到达。
请注意,此 m 服务器丢失系统中没有封闭式表达式。值可以从表格中计算出来。此系统通常用于根据呼叫率和呼叫持续时间来确定电话通道的大小。
我们对 M/M/1 队列的讨论可以通过允许到达率和服务率依赖于队列状态来推广。也就是说,到达过程是参数为 的泊松过程,服务要求是参数为 的指数分布。下标 n 指的是队列中的作业数。如果队列状态为 n=k,则到达的概率为
并且离开的概率(假设队列不为空)为
到达或离开的概率仅通过参数 和 依赖于队列状态。
由于泊松过程的无记忆性,在时间 t 队列处于状态 n=k 且在给定队列在间隔开始时处于状态 k 的情况下,在间隔 h 内有到达或离开的概率是独立的。因此,下面的状态转移图描述了马尔可夫链。
通过观察发现的平衡方程要求“概率流出”速率等于流入速率
并且归一化方程又是
这些方程可以通过考虑简单 M/M/1 队列中间隔 h 内到达、离开和无变化的概率来更正式地找到。
以及对于 k=l,
将 P(1) 替换得到
以及一般情况下,
使用归一化方程找到常数 P(0)。将 P(k) 替换得到
或
结合得到一般解
Kleinrock 讨论了平衡状态下生死队列的几种变体。两种情况在对计算机系统建模时特别有用。它们是“无限服务器队列”和“有限种群模型”。
在无限服务器队列中,当作业到达队列时,总会有一个空闲的服务器。
如果队列中有 2 个作业,则服务率为 (我们可以将其视为 2 个泊松服务过程的叠加,每个过程的速率为 ),并且如果队列处于状态 n=k,则服务率为 。请注意,这意味着服务完成之间的平均时间为
当队列状态为 n=k 时。很明显,这个排队系统也可以解释为有一个单一服务器,当有更多作业等待服务时,它的服务率会线性增加。
对于这个队列,
并且状态转移图是
解简化为
并且
现在
因此
结合得到
队列中的平均数量为
或者令 r = k-1
平均响应时间 T 通过应用 Little 公式 找到,得到
或
这是预期的,因为没有作业必须等待才能开始接收服务。
无限服务器队列通常用于对计算机系统建模,以表示用户终端组或表示不涉及排队或作业之间冲突的随机延迟。
排队网络是通过将一个队列的输出连接到另一个队列的输入来构建的。如下所示。
请注意,单个队列可以从多个队列的输出中馈送,并且队列的输出可以被拆分为多个队列的输入流。每个队列形成网络的“节点”,这些节点可以编号为 1、2…M,其中 M 是网络中的节点数。“路由概率”是从网络的节点 i 出发立即到达节点 j 的概率。
排队网络可以用来模拟多个交互设备的系统,每个设备都可以被建模为一个队列。例如,由 CPU 和磁盘组成的简单计算机系统可以用一个 2 队列网络来表示。
排队网络可以是“开放”的或“封闭”的。在开放网络中,作业从外部源到达某些节点,并且可以从某些节点离开网络(到某个吸收目的地或“汇点”)。网络中的作业数量可以变化,并且源具有无限的供应。在封闭网络中,固定数量的作业在网络的节点之间循环;没有新作业进入网络,也没有作业离开网络。
封闭网络在对计算机系统建模方面特别成功。两种最常用的模型是中央服务器模型和机器维修员模型。
下面显示了中央服务器排队网络。
这里节点 1 表示 CPU,节点 2 到 M 表示系统输入/输出 (I/O) 设备——通常是磁盘控制器。作业被视为在 CPU 上接收服务,然后以概率 路由到 I/O 设备 i。在 I/O 设备上接收服务后,作业返回到 CPU。在这个模型中,计算机系统对作业的处理由作业多次访问 CPU 和 I/O 设备来表示。从 CPU 返回自身的路径(以概率 )代表系统中一个作业的完成和另一个作业的同步开始。
中央服务器网络特别适用于对多道程序计算机系统的内部资源(CPU 和磁盘)进行建模。在这些系统中,为了提高系统效率,多道程序级别(内存中同时运行的作业数量)通常限制为少量作业。在中度到重度负载下,系统多道程序级别通常处于或接近此限制。因此,假设网络中的作业数量是恒定的,这很好地近似于实际系统。
机器维修员模型最初是在运筹学中开发的,通常用于表示交互式计算机系统。该网络,如下图所示
有一个多服务器节点,表示用户终端。另一个(系统)节点表示其他系统资源。这些可以任意连接,尽管通常使用中央服务器网络的变体。作业从终端节点开始,然后进入系统,在系统节点之间循环,然后返回到终端节点。从作业离开终端节点到它返回的时间是系统响应时间,它在终端节点花费的时间称为用户思考时间。网络中的作业数量与终端节点上的服务器数量相同。因此,没有作业等待开始在该队列中接收服务,并且它的服务时间与思考时间相同。
开放网络最常用于对具有可变作业数量或恒定作业到达率的计算机系统进行建模。批处理系统和通信网络通常是这种类型。
许多交互式计算机系统的一个特别有用的模型是下面所示的终端驱动的系统。
在这个模型中,作业的数量等于终端的数量(即每个终端有一个作业)。作业被可视化为在用户按下“回车键”时离开“终端”,在系统中经过各种设备进行处理,然后返回到终端节点。从作业离开终端节点到返回的时间是系统响应时间。作业在终端等待的时间(即从响应到下一个系统输入的时间)是用户“思考时间”。
Let: denote the rate with which jobs enter the system (system throughput); R denote the system response time; Z denote the user think time; N denote the number of terminals (or jobs) in the System.
现在我们将 Little 公式应用于包含终端和系统(大写 S)的 SYSTEM(所有大写字母)。
对于 SYSTEM,每个作业在终端平均花费时间 Z,在系统中平均花费时间 R,在 SYSTEM 中平均花费时间 Z + R。然后它离开并立即返回。平均作业吞吐率为,系统中的作业数量固定为 N。
因此,根据 Little 公式
或
现在我们试图找到响应时间 R 和吞吐率 的界限。
设系统中的各种设备编号为 1,2,...M,设 是作业从设备 i 接收的平均总服务量。注意,当作业在系统中时,它实际上可能多次访问设备 i,在这种情况下 是它在每次访问时接收的服务量的总和。设 是作业在每次访问设备 i 时接收的平均服务量。如果 与 i 无关,那么
是作业访问设备 i 的平均次数。
如果只有一个终端,因此系统中只有一个作业,R 仅仅是作业从每个设备需要的服务量的总和。这是可能的最小响应时间。因此
由于每个设备的利用率不能超过 100%,因此设备 i 的吞吐率 充其量为 。因此,
并且由于作业在每次通过系统时平均访问设备 i 次,
因此,
将此公式代入响应时间表达式得到下界
为了找到 R 的上界,我们注意到作业在任何设备 i 上花费的最长时间将发生在每次访问时,它必须等待其他 N-l 个作业完成服务才能接收其服务。因此,
下面显示了这些响应时间与系统中终端数量的关系。虚线显示了典型的系统响应时间函数。
之间的区域通常被称为系统的可行响应时间区域。在实践中,随着终端数量的增加,响应时间变得渐近于直线
这是 最左边的线,也是 的最大值的线。对应于这条线的设备被称为系统瓶颈,其他设备的其他线是由于这些设备造成的潜在瓶颈。上面提到的瓶颈和潜在瓶颈很容易找到。观察到每个都是一条直线,它在水平(终端)轴上的截距为 ,斜率为 。由于 随着线从左到右移动而变小,它们看起来像是“落下”。
从 中,对于所有 i,我们注意到
其中 是最大 的设备的总服务时间。这是系统可能的最大吞吐量。
重新排列得到 的表达式
我们注意到系统中存在 N 个作业。因此,
类似地,由于 ,我们有:
下图显示了这些系统吞吐量与终端数量关系的界限。
点
在前面两张图中显示,被称为系统的饱和点。它解释如下。
当一个终端连接到系统时,作业永远不会因为等待其他作业在设备上接收服务而被延迟。因此,它在系统中花费时间 ,吞吐量为 。如果随着终端数量的增加,每个进入系统的作业都没有因为等待其他作业被服务而被延迟,那么每个作业只会在系统中花费时间 。响应时间将为 ,吞吐量将沿线 增加。
然而,当终端数量 N 变得等于 N* 时,系统吞吐量将达到 ,瓶颈设备将达到 100% 的利用率。此时它“饱和”。如果此时再添加一个作业进入系统,那么作业只能在另一个作业开始服务时到达瓶颈设备。因此,每个作业都必须等待一段时间才能开始自己的服务。因此,对于每个超过 N* 的终端,最小可能的响应时间增加 ,最小响应时间将沿线 增加。
前面两张图中的界限提供了关于我们开始修改系统配置时系统行为的见解。
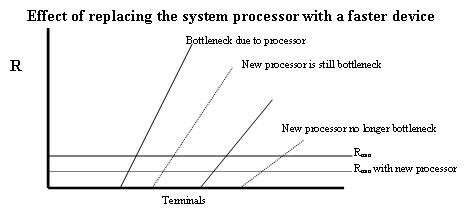
例如,考虑一个计算机系统,其中处理器处理终端 I/O 流量并且是系统瓶颈。设 是作业在处理器上接收的平均处理时间。如果处理器被更快的设备替换,就会减少。因此延迟 会减少,并且由于处理器造成的“潜在瓶颈”向右移动。如果它移动足够远,以至于另一个设备成为最左边的潜在瓶颈,那么该设备就成为新的瓶颈。如果它没有移动到其他潜在瓶颈的右边,那么它仍然是瓶颈,但是可以获得更低的响应时间和更高的吞吐量。下图显示了这些更改对响应时间渐近线的影响。
如果将终端 I/O 处理卸载到前端处理器(FEP)上,则会出现更有趣的情况。这也减少了 并将处理器瓶颈向右移动,但它向系统添加了一个新设备和相应的潜在瓶颈。
设 是处理器花费在 I/O 上的时间。那么 将减少 。如果 FEP 比处理器慢,那么 将大于 ,并且 将增加 - 。如果 FEP 更快, 将减少 。
如果系统负载很重,以至于处理器是控制响应时间并限制吞吐量的活动瓶颈;只要系统吞吐量将增加,即使 FEP 比处理器慢得多。当处理器瓶颈向右移动时,哪个设备成为新的系统瓶颈取决于 和系统中的其他设备的值。
饱和于
问题
Can we get 1 sec response time? – No. Can we get 2 sec response time with 30 terminals? – Yes. Can we get 2 sec response time with 35 terminals? – No.
CPU 是瓶颈。使用更快的 CPU 来获得更好的性能。
更快的 CPU 导致更短的处理时间(比如 0.75 秒)。
导致性能大幅提升。
更快的磁盘…
…会稍微好一点,但效果不大。
稍微更快的 CPU, vcxc = 0.6 …
…CPU 仍然是瓶颈。
然而,如果 vcxc = 0.4 …
…那么磁盘现在是瓶颈,CPU 的进一步改进帮助不大。
添加第二个 CPU…
边界模型独立于内部系统结构。该模型依赖于每个设备上作业所需的总服务。因此,边界模型可以表示为串行系统。
total service = vixi = Ti is easy to measure Ui is easy to measure is easy to measure vi is usually hard to measure xi is usually hard to measure