计算机图形学概念/输出空间/数字图像表示

现在我们已经涵盖了如何表示图像和颜色的基础知识，我们可以将这些信息组合成更详细的数字图像表示图。我们之前注意到，数字图像只是一组颜色值，现在我们了解了如何在 RGB 颜色空间中将颜色表示为数字，我们可以将这些信息结合起来以获得更详细的图像。

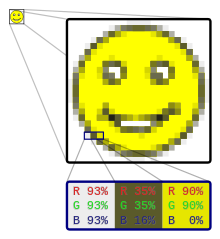
正如您所料，图像的数字表示只是一个 RGB 值三元组数组。具体来说，可以将图像视为这些颜色值的矩形网格。如果我们处理的是我们希望为 800 x 600 像素的图像，那么我们将有一个数组，该数组在图像的宽度上具有 800 个 RGB 颜色值，在图像的长度上具有 600 个 RGB 颜色值。

正如您所料，通过其 (x,y) 坐标引用任何给定像素很方便。在这个坐标系中，(0,0) 是左上角的像素，(宽度，高度) 是右下角的像素，其中宽度和高度分别表示图像的宽度和高度（使用上面的例子，它们将分别为 800 和 600）。因此，当您水平横跨图像时，x 值会增加，而当您向下移动图像时，y 值会增加，这在最初可能违反直觉。

这是一个相当任意的组织（事实上，在某些图像格式中，(0,0) 是左下角的像素，正如您从熟悉的笛卡尔坐标系中所期望的那样），但这是我们在整本书中将假设的组织，并且它也是实践中最广泛使用的组织。从计算机设计师的角度来看，使用这种组织有一个实际的好处，但计算机图形程序员很少看到它的好处。好处是：当计算机显示器显示图像时，它会从左到右，从上到下，横跨显示器上所有像素扫描光束。因此，在将图像发送到显示器时，首先给它绘制的内容更有意义。

还值得注意的是，从一种表示形式转换为另一种表示形式很容易。例如，如果您希望将屏幕视为具有熟悉的坐标系，那么您可以简单地按照您喜欢的方式编写代码，然后在显示到屏幕之前重新排序行。另一种选择是将您想要访问的每个 y 坐标替换为 (height-y)。因此，当您尝试访问您认为是屏幕底部的行 (y=0) 时，您将改为访问 (y=800-0=800)，这是计算机显示器认为的屏幕底部行。最后，像素必须朝着一个方向或另一个方向移动，而这是一种熟悉且常用的格式。

在计算机内存中，图像以这种非常直接的方式布局，作为一个连续的内存块。每个像素都为表示其颜色分量的三个数字分配了足够的存储空间，并且图像中的第一个像素 (0,0) 是内存块中的第一个像素。下一个最高内存地址是行中的下一个像素 (1,0)，依此类推。最终，内存块中的最后一个像素是位于位置 (宽度，高度) 的像素。

例如，假设我们有一个内存中的图像，大小为 800 x 600 像素，图像的第一个像素位于内存地址 100，并且每个 RGB 分量的尺寸由 r 给出。然后地址 100 处的 r 个字节是 (0,0) 处的像素，地址 100+r 处的 r 个字节是 (1,0) 处的像素，地址 100+2*r 处的 r 个字节是 (2,0) 处的像素。如果我们想要访问 (5,5) 处像素的像素数据，我们需要访问地址 100+5*宽度*r+5*r 处的 r 个字节。也就是说，我们需要将第一个 5 行的字节数 (5*宽度*r) 添加到基地址，再加上该像素所在行的字节数。一般来说，我们可以通过访问 baseAddress+y*宽度*r+x*r 来访问内存中的像素 (x,y)。这个公式不必记住，但重要的是要理解内存中的图像数据不是二维的，而是一维的，我们只是通过解释方式赋予数据二维的组织。