圆锥曲线/圆

圆是最简单、最著名的圆锥曲线。作为圆锥曲线，圆是垂直于锥体轴的平面与锥体的交点。

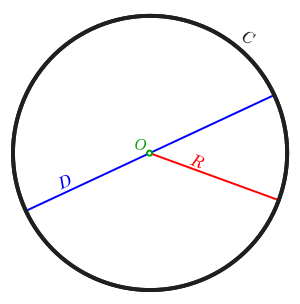
圆的几何定义是所有点到一个固定点$(h,k)$的距离为一个常数$r$的点的轨迹，形成圆周 (C)。距离$r$是圆的半径 (R)，点$O=(h,k)$是圆的中心。直径 (D) 是半径长度的两倍。

圆的示意图，圆周 (C) 为黑色，直径 (D) 为青色，半径 (R) 为红色，中心或原点 (O) 为洋红色。

方程

标准形式

以$(h,k)$为圆心，$r$为半径的圆的标准方程是

$(x-h)^{2}+(y-k)^{2}=r^{2}$.

在圆心位于原点的最简单情况下，该方程只是勾股定理的重新陈述

$x^{2}+y^{2}=r^{2}$

一般形式

圆方程的一般形式是

$x^{2}+y^{2}+2gx+2fy+c=0$，其中

<-g,-f> 是圆的圆心。

极坐标

在圆心位于原点的圆的情况下，圆的极坐标方程非常简单，因为极坐标本质上是基于圆的。对于半径为$a$的圆，

$r=a$.

在圆心位于任意位置的更复杂情况下，该方程是

$r^{2}-2rr_{0}\cos(\theta -\varphi )+r_{0}^{2}=a^{2}$,
其中$r_{0}$是圆心到原点的距离，$\varphi$是指向圆的角。

有许多情况允许简化该方程。如果圆上的一个点与原点相切，则其极坐标方程可能只包含一个三角函数。

.....

参数方程

当圆的方程用参数 $t$ 参数化时，方程变为

$x=h+r\cos t$,
$y=k+r\sin t$.

示例

找到以下圆的圆心和半径：x²+y²+8x-10y+20=0 通过以下步骤

x²+y²+8x-10y+20=0
x²+y²+8x-10y= - 20
(x²+8x)+(y²-10y)= - 20
+16 +25 +16+25
(x²+8x+16)+(y²-10y+25)=21
(x+4)²+(y-5)²=21

因此
C(-4,5) 半径=$radical(21)$