密码学/基本公钥示例

公钥密码学的基本工作原理最好用一个例子来解释。下面的工作涵盖了简单密钥的制作以及明文样本的加密和解密。出于必要性，这个例子被大大简化了。

基本公钥摘要

公钥加密用于互联网安全链接，例如，当浏览器打开银行网站或使用信用卡的网站时。此类地址以 https 为前缀，而不是仅仅使用 http。RSA-OpenSSL 就是这样的加密系统。在这个安全网站标记的例子可以在本页面的地址中看到；此维基教科书页面（当用户登录时）显示 https 前缀或其他一些特定于浏览器的标记，表明它被认为是安全的。
每个网站都有自己的 加密密钥 和 解密密钥，分别称为公钥和私钥。这些本质上都是非常大的数字。这些密钥总是不同的，从而产生了 非对称加密 的术语。实际上，每当我们说密钥时，我们指的是一对组成密钥的数字；一个用于幂运算的密钥数字，另一个是用于该运算的模数。对于不熟悉模运算的人来说，请参阅维基教科书页面 高中数学扩展/素数/模运算，以获得一个简单易懂的描述。

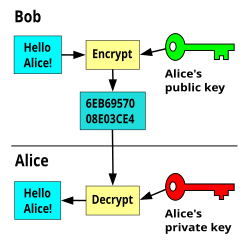
公钥对任何人都公开可用，但私钥则不公开。接收方站点将他的公钥提供给消息发送方，或者通过使用公共目录。对于每次消息传输，发送方都使用此密钥来生成代码。这样，只有接收方的私钥才能解密它。在下面的文本中提供了一个实际的例子，并且可以在图 1 中看到基本过程。
实际上，用于公钥加密的两个密钥形成一个 可逆函数。如果系统设计者打算这样做，你也可以用私钥加密，用公钥解密。当然，对于不那么公开的使用，公钥也可以像私钥一样被保密。这种密钥对的可逆性在测试数字证书时很有用，其中颁发者用他的私钥加密证书，以便接收者可以用他公开的公钥来测试其真实性。
使用的数字被故意设置得非常大，这使得从公钥中获取私钥的任务对于黑客来说过于困难。它涉及对非常大的数字进行因式分解，非常耗时。
这类系统虽然不完美，但只要破解它们所需的时间远远超过数据感兴趣的期限，它们仍然很有用。估计破解某些此类代码所需的时间是数千年。
签名的数字证书在提供公钥时有助于验证用户站点的身份。浏览器会采取步骤来确认其有效性。
公钥系统的主要优点是管理负担很低。发送消息到站点所需的一切信息都可以在公共目录中找到，或者作为建立链接的一部分公开发送。
公钥密码学的主要缺点是它对于现代互联网使用来说太慢了。因此，互联网最常使用 对称加密 来完成主要任务；（一种不同的方法，它使用一个共同的密钥来进行加密和解密）；它只是使用公钥方法来隐藏对称密钥，同时将其发送到远端。
黑客使用多种方法来破解编码
- 暴力破解 密钥指的是尝试私钥的所有可能组合，同时将其与相关的密文进行测试。这种测试非常耗时，因为每次迭代都需要字典检查或人工干预来决定是否出现了明文。此外，数字非常大，因此这种方法很少有什么意义。
- 数学攻击指的是找到两个素数，它们的乘积构成了公开可用的密钥的模数。如果能够找到它们，那么它将简化私钥的查找（稍后详细介绍）；这种方法的优点是计算机可以自主完成这项任务，不需要太多干预。截至撰写本文时（2014 年），Lenstra 等人打破密钥的数学攻击的记录是 2009 年 12 月 12 日，当时一个 RSA-768 位模数（232 个十进制数字）被使用一种叫做一般数域筛法（GNFS）的方法进行分解。这个过程需要两年的合作以及数百台计算机。（参见：http://eprint.iacr.org/2010/006.pdf）如今，大多数使用的加密密钥远大于被破解的那个，一个 1024 位或 2048 位的 SSL 证书密钥仍然被认为对数学攻击是相当安全的。请注意，破解此类密钥的难度随着密钥长度的 指数级 增加。
- 然而，成功的入侵历史并没有涉及代码破解，而是黑客入侵服务器以获取其数据和私钥。其他利用漏洞依赖于个人的安全疏忽或程序缺陷。例如，最近的一次 SSL 利用漏洞（2000-2014 年？），其访问数据并不是通过代码破解，而是通过一个程序缺陷，该缺陷允许发送方从接收方的服务器下载内存块内容。SSL 的目的是允许接收方服务器的一些文本作为消息接收和成功解密的证明返回。为此，发送方可以指定要返回的文本长度，通常是头部，在任何情况下都小于 64K 位。该缺陷的核心在于，如果发送了一个非常短的消息，但发送方要求返回比发送的消息更大的块，则有缺陷的程序会照做，因此返回了包含其他安全材料的数据。每隔几秒重复此过程，允许黑客积累大量数据块。据说这个问题已经得到纠正，但据说在约四年的时间里，任何知道它的人都可以利用它。

创建站点 B 的公钥

公钥对所有人公开，用于加密发送给密钥所有者的消息.

每个站点的计算机都会生成两个非常大的素数，由于它们是所有后续操作的基础，因此这些数字永远不会向任何其他人透露。（素数是指除了自身和 1 之外没有其他因子的数字）。
这两个数字相乘得到所有站点计算中使用的模数。主要公钥也是从这些素数中推导出来的，并确定明文数字将被提升到的指数。
此公钥在目录和证书颁发机构中提供，因此当发送方想要通过公钥密码学加密消息时，他可以轻松地使用 接收方 的公钥（和模数）来实现。每个站点的公钥集都可以被设计为几乎肯定与其他所有站点不同。

为了说明这一点，让我们用非常小的数字来代替大型素数，为想要接收消息的人创建一个简单的例子。

假设两个秘密持有的素数是

p = 5  ,  q = 11

那么将被使用的运算的模数由它们的乘积给出

m = 5  x  11 = 55    (the modulus of the arithmetic to use)

加密密钥的计算方法如下：首先，使用这两个素数，计算函数

   f(n)  = (p-1) x (q-1)
∵ p = 5 and q = 11    
∴ f(n) = (5-1) x (11-1)
∴ f(n) =  40

然后，
选择任何一个与 f(n) 互质且小于它的数字。

（当两个数字除了 1 之外没有其他公因子时，它们被称为互质。此术语也称为互质或互素）。

 The possible choices become:
 3, 7, 9, 11, 13, 17, 19, 21, 23, 27, 29, 31, 33, 37, and 39.

 Say we select the public encrypt exponent =  7

然后，接收方站点的公钥可以安全地发布给全世界，即

(7, 55) as (encryption exponent, modulus)
(In practice the numbers would be very much larger)

实际使用的数字非常大。例如，对于 1024 位的 RSA 加密，此数字是模数的位数；这相当于大约 308 位的十进制数，或 256 个十六进制数字。最常选择的公共指数具有 65537 的整数值。选择此指数是因为它比其他一些选择产生更快的加密速度；也就是说，由于它在二进制形式中的大量零计数（10000000000000001），它适合使用二进制移位方法进行快速处理。它在别处被称为费马数 F4。尽管人们偏爱相同的指数，但请记住，公钥集的另一部分是模数，而模数将因用户而异，因为可用的素数数量非常多。

创建站点 B 的私钥

站点 B 在解密发送给它们的消息时使用，该消息使用站点 B 的公钥加密.

私钥对用于解密消息，并且只有当使用同一站点的公钥加密消息时，此密钥才有效。也就是说，站点 B 的公钥是从目录中获取的，然后由站点 A 用于加密发送给它们的消息。当消息到达站点 B 时，站点 B 使用它自己的私钥进行解密。

继续以上面的简单示例，站点 B 的私钥是从其公钥中生成的，方法如下。

   私钥解密指数 = (公钥加密指数)-1 Mod f(n)
∵ 公钥加密指数 = 7， 且 f(n) = 40
∴ (私钥解密指数 x 7) Mod 40 = 1
∴ 私钥解密指数 = 23


  站点 B 的私钥对是：
  (23, 55) 作为 (解密指数，模数)

有些人可能已经注意到，加密指数和解密指数可以是相同的数字。这种情况必须通过刻意测试来避免，因为黑客很可能在攻击过程的早期测试这种可能性。在上面的例子中，如果选择 9、11、21、33 或 39 作为公钥，而不是其他数字，就会出现这种情况。不要以为预测这种错误很简单，请注意，即使在这种情况下，既是互素数又是素数的互素数（例如：导致：11 * 11 = 1 mod 40），以及那些互素数但本身不是素数的互素数（例如：9、21、33 和 39），都可能导致这种不安全的状况。

使用长素数时，模数 (m)（它们的乘积）会长得多，但很明显，如果黑客能够找到两个秘密素数作为起点，他仍然可以获得私钥。公钥和与之一起使用的模数都提供给所有需要它进行加密的人，因此数学攻击的负担就减少到将模数分解成这两个秘密素数的难度。对于上面显示的简单示例 (m=55)，这项任务非常简单，但对于非常大的数字，这项工作就很长，让人望而却步。

私钥的原生格式实际上是 base-64（一种字符集，每个字符只需要 6 位，而不是十六进制的 4 位或 ASCI 字符代码的 7 位）。与公钥字符串不同，1024 位 RSA 加密的实际私钥字符串的布局包含私钥详细信息、公钥详细信息以及生成它们时使用的秘密数字，以及其他一些数字和标头。私钥指数与公钥指数不同，它很长，相当于 256 个十六进制数字的长度。两个秘密素数分别是 128 个十六进制数字的长度。十进制等效长度为私钥指数（和模数）的 308 位，以及每个秘密数字的 154 位。

对模数进行因式分解

黑客想要在没有任何其他算法辅助的情况下对模数进行因式分解，他们可以简单地用一系列递增的素数除以模数，直到余数为零。然后，两个素数就知道了。但是，在如此大的模数中，素数的数量也非常多。一般来说，以下近似值，称为素数定理，给出了数字 x 中素数的数量为

   素数的数量 ≅ x/(logx - 1)
   现在，64 位空间相当于大约 20 位数字
∴ 素数的数量 ≅ 4 * 1017
   然后假设每秒 100 万次计算（对于大多数人来说，这是一个非常乐观的假设）
   测试所有素数的时间 ≅ 13,500 年

这里给出的示例仅限于 64 位，因为更具代表性的数字（128 位、256 位、512 位、1024 位和 2048 位计算）对于大多数计算器来说都太大。请参阅 DigiCert 的 破解 2048 位证书背后的数学原理，以了解更多详细信息。

此示例不考虑使用改进的因式分解方法，而这些方法在文献中经常出现。目前（2014 年），这些方法中最好的是通用数域筛法 (GNFS)，用于建立 2009 年 12 月的记录.

为了更详细地说明改进方法，很明显，从表格素数列表开始可以加快处理速度。这一点，以及针对未来需要计算出的乘积表，也能比在运行时进行计算快得多。因为很明显，对于大量此类破解问题，一半的解将位于尝试值的前半部分，一半位于后半部分，所以习惯上将对整个集合隐含的素数定理所隐含的一半集合的预期解决时间表达为一半。

使用 B 的公钥进行加密

假设公钥对属于站点 B。还假设由数字“2”表示的明文字符要由站点 A 加密并发送给收件人站点 B：站点 A 使用站点 B 的公钥对进行加密。

   假设明文=2
   密文 = 明文公钥加密指数 Mod n
∵ 公钥加密指数 =7， 模数 = 55
∴ 密文 = 27 Mod 55 = 128 Mod 55
∴ 密文 = 18

使用示例中使用的非常小的数字，破解代码将相对简单。但是，对于素数p和q的非常大的值，并且在不知道私钥的情况下，这项工作变得非常困难。在某些情况下，即使对于大量计算机来说，这项任务也需要相当长的时间。

公钥加密不会掩盖所用字符的相对频率。由于这会提高破解代码的可能性，因此被认为是此类系统中的一个缺陷。因此，明文字符在加密之前被排列成组以隐藏它们的使用频率；这些组非常大，限制是加密的数字的大小必须小于正在使用的模数。

使用 B 的私钥进行解密

使用上述特定示例进行解密的方法如下：对于接收到的密文 = 18

   对于来自上一节的密文=18
   明文 = 密文私钥解密指数 Mod n
∵ 私钥解密指数 = 23， 模数 = 55
∴ 明文 = 1823 Mod 55 = 74347713614021927913318776832 Mod 55
∴ 明文 = 2（你只能用 Windows 科学计算器来确认这一点）

请注意，明文值2已恢复，这是所需的结果。

例外情况

一些使用非正确私钥的尝试仍然会成功。需要考虑例外情况。例如，在上述情况下，使用解密指数 =3 也会产生正确的结果。见下文

   对于来自上一节的密文=18
   明文 = 密文私钥解密指数 Mod n
∵ 黑客尝试的解密指数 = 3， 模数 = 55
∴ 明文 = 183 Mod 55 = 5832 Mod 55
∴ 明文 = 2 也是正确的结果。
请注意，每个 (N^7Mod55)^3Mod55 == (N^7Mod55)^23Mod55)

在实际环境中，在选择密钥时，需要进一步考虑此类问题。

互联网速度折衷方案

由于公钥加密和解密非常慢，因此它们不适合以其原生形式用于互联网。事实上，非对称公钥加密仅用于互联网通信的一小部分。此类系统是混合系统。所使用的方法的总结如下

要安全传输的文本不是通过公钥密码术进行加密的，而是通过使用对称密钥加密进行加密的。这通常是 128 位密码，但可以更大。对称密钥方法需要两个站点使用相同的密钥。为此，一个站点必须在某个阶段生成密钥，然后将其副本发送到另一个站点。
此对称密钥不是公开发送到远端，而是首先使用公钥方法对其进行加密后保持安全。为此，将使用目标站点的公钥。
接收者使用其私钥解密此密文，并恢复对称密钥值。然后，他用它解密主对称密文。
对称加密密钥在当前会话结束时被丢弃，而非对称公钥可能会被丢弃，也可能不会被丢弃，这取决于所使用的系统。密钥的较短寿命可以减少网络攻击期间成功恢复密钥的可能性，以及随后在较晚时间对记录的流量进行解码的可能性。考虑到这一点，短会话可能比长会话更安全，当然前提是丢弃意味着从内存中完全删除，而不仅仅是普遍的删除。

目前用于互联网浏览器的系统是传输层安全 (TLS) 及其前身安全套接字层 (SSL)。在维基百科的 安全套接字层中可以找到这些内容的完整描述。

请注意，在双工系统中，即通常的双向发送系统，将有两种这样的过程。一个起源于每端。用于发送和接收的密钥集（对于非对称和对称加密系统）都是不同的。

消息认证

如果外部人员可以在传输过程中更改消息，或者从一开始就错误地代表自己，安全性就会崩溃。为了克服这些风险，数字证书被设计出来。为了进一步确保证书来自用户尊重的机构，证书被赋予了数字签名。在众多方法中，一种方法是数字签名算法 (DSA)，它是数字签名标准 (DSS) 的基础。

这些证书不仅仅是简单的文本消息，当然可以被模仿，而是使用基于消息内容的计算值。认证的整个基础依赖于这些哈希算法的设计属性以及断言其价值的人的完整性。它们的属性包括

敏感性：它们非常敏感。哈希算法输入的微小变化总会对其输出值产生非常大的变化。
特异性：它们非常特定。虽然这取决于使用的哈希算法，但两种不同的输入几乎不可能产生相同的输出。当这种情况发生时，例如每数十亿次发生一次，它被称为冲突。
不透明性：无法从输出值中找到输入值。这是因为算法的高度复杂性，尤其是因为大量使用了模算术的单向函数。
保密性：一些哈希算法可供公众使用，但专有利益可以创建自己的算法。大多数人可以使用的一些算法包括 MD5、SHA1、SHA2、SHA3 等。MD5 已经被破解。SHA1 是当前大多数证书的基础，已被弃用，因为它在使用上过于复杂。

哈希值由发送方计算，并与接收端计算的值进行比较，两者必须匹配才能被接受。与加密本身一样，哈希值难以逆向工程，也就是说，外部人员无法在任何有用的时间段内创建新的或更改的消息来表示现有的哈希值。因此，它们提供了验证消息内容自证书发布以来未更改的基础。

证书本身会根据浏览器存储区中已知的根证书进行测试，以确保证书来自已知的可靠来源。如果证书使用仅发行机构知道的私钥进行秘密签名，则可以通过使用其公钥解密签名来验证证书。也就是说，由于该过程是可逆的，因此可以验证来源。

用于这些任务的实际过程比摘要中暗示的要复杂得多，涉及许多长位计算，但该系统的强度可能无法满足怀疑者的要求，直到看到这些计算。请参阅 PDF 文件 加密和数字签名工作原理 并阅读数字签名机制示例部分以获取此类描述。

证书测试和其他事项的处理过程通常由浏览器为用户总结。浏览器将清楚地指示它们是否认为连接是安全的。这些指示中最常见的是在屏幕上的某个位置添加一把锁，并将网站的http 地址标题修改为https。一些浏览器，如 Opera，还会添加其他信息，例如颜色编码，以表示安全级别。

另见

高中数学扩展/素数/模算术 : 你可能已经忘记的东西。

进一步阅读

仿生水牛技术说明 35：加密和数字签名工作原理 清晰地描述了数据加密标准 (DES)、RSA 公钥标准和数字签名算法 (DSA) 的工作原理，并附有丰富的数学说明。
数字签名算法
破解分解记录 : DigiCert 对破解 2048 位证书的估计背后的数学原理。
RSA 分解挑战: 包含迄今为止在素数分解方面的进展表。
RSA 密钥布局: 显示 1024 位 RSA 加密的私钥和公钥的精确布局的页面。