数据编码理论/霍夫曼编码

从文本 "this is an example of a huffman tree" 中生成的确切频率生成的霍夫曼树。每个字符的频率和代码如下所示。使用此代码对句子进行编码需要 135 位，不包括树的空间。

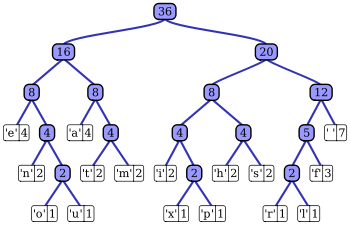
字符	频率	代码
空格	7	111
a	4	010
e	4	000
f	3	1101
h	2	1010
i	2	1000
m	2	0111
n	2	0010
s	2	1011
t	2	0110
l	1	11001
o	1	00110
p	1	10011
r	1	11000
u	1	00111
x	1	10010

在计算机科学和信息论中，霍夫曼编码是一种用于无损数据压缩的熵编码算法。该术语指的是使用变长码表来编码源符号（例如文件中的字符），其中变长码表是根据源符号每个可能值的估计出现概率以特定方式推导出来的。它是由 David A. Huffman 在麻省理工学院攻读博士学位期间开发的，并于 1952 年发表在论文 "A Method for the Construction of Minimum-Redundancy Codes" 中。

霍夫曼编码使用一种特定方法来选择每个符号的表示，从而产生一个前缀码（有时称为“前缀自由码”）（即，表示某个特定符号的比特串永远不会是表示任何其他符号的比特串的前缀），该前缀码使用比用于不太常见的源符号的更短的比特串来表达最常见的字符。霍夫曼能够设计出此类型最有效的压缩方法：当实际符号频率与用于创建代码的频率一致时，将单个源符号映射到唯一的比特串的其他映射不会产生更小的平均输出大小。后来发现了一种方法可以在输入概率（也称为权重）排序的情况下以线性时间完成此操作。

对于一组具有均匀概率分布且成员数量为 2 的幂的符号，霍夫曼编码等同于简单的二进制块编码，例如 ASCII 编码。霍夫曼编码是一种创建前缀码的非常普遍的方法，以至于术语“霍夫曼码”被广泛用作“前缀码”的同义词，即使这样的码不是由霍夫曼算法生成的。

虽然霍夫曼编码对于已知输入概率分布的符号按符号编码（即不相关符号流）是最佳的，但其最优性有时会意外地被夸大。例如，算术编码和 LZW 编码通常具有更好的压缩能力。这两种方法都可以组合任意数量的符号以实现更有效的编码，并且通常适应实际的输入统计数据，后者在输入概率未知或在流中变化很大时很有用。一般来说，改进来自于输入符号相关（cat 比 cta 更常见）。

历史

1951 年，David A. Huffman 和他的麻省理工学院信息理论同学可以选择一篇学期论文或期末考试。教授 Robert M. Fano 指派了一篇关于寻找最有效二进制码的论文。霍夫曼无法证明任何代码是最有效的，正要放弃开始准备期末考试时，他突然想到使用频率排序的二叉树，并很快证明了这种方法是最有效的。

这样做，这位学生超过了他的教授，他的教授曾与信息论发明家克劳德·香农合作开发了一种类似的代码。霍夫曼通过自下而上而不是自上而下构建树，避免了次优香农-法诺编码的重大缺陷。

问题定义

非正式描述

给定

一组符号及其权重（通常与概率成正比）。

查找

具有最小预期码字长度的前缀自由二进制码（一组码字）（等效地，具有最小加权路径长度的树）。

形式化描述

输入.
字母表 $A=\left\{a_{1},a_{2},\cdots ,a_{n}\right\}$，它是大小为 $n$ 的符号字母表。
集合 $W=\left\{w_{1},w_{2},\cdots ,w_{n}\right\}$，它是（正）符号权重（通常与概率成正比）的集合，即 $w_{i}=\mathrm {weight} \left(a_{i}\right),1\leq i\leq n$。

输出.
代码 $C\left(A,W\right)=\left\{c_{1},c_{2},\cdots ,c_{n}\right\}$，它是一组（二进制）码字，其中 $c_{i}$ 是 $a_{i},1\leq i\leq n$ 的码字。

目标.
令 $L\left(C\right)=\sum _{i=1}^{n}{w_{i}\times \mathrm {length} \left(c_{i}\right)}$ 为代码 $C$ 的加权路径长度。条件：对于任何代码 $T\left(A,W\right)$，$L\left(C\right)\leq L\left(T\right)$。

样本

输入 (A, W)	符号 (ai)	a	b	c	d	e	总和
	权重 (wi)	0.10	0.15	0.30	0.16	0.29	= 1
输出 C	码字 (ci)	000	001	10	01	11
	码字长度（以比特为单位） (li)	3	3	2	2	2
	加权路径长度 (li wi )	0.30	0.45	0.60	0.32	0.58	L(C) = 2.25
最优性	概率预算 (2-li)	1/8	1/8	1/4	1/4	1/4	= 1.00
	信息量（以比特为单位） (−log2 wi) ≈	3.32	2.74	1.74	2.64	1.79
	熵 (−wi log2 wi)	0.332	0.411	0.521	0.423	0.518	H(A) = 2.205

对于任何双唯一的代码，这意味着代码是可唯一解码的，所有符号的概率预算之和总是小于或等于 1。在这个例子中，总和严格等于 1；因此，代码被称为完整代码。如果情况并非如此，则始终可以通过添加额外的符号（以及相关的零概率）来推导出等效代码，从而使代码完整，同时保持其双唯一性。

如香农（1948）所定义，每个符号 a_i 的信息量 h（以比特为单位）具有非零概率，为

$h(a_{i})=\log _{2}{1 \over w_{i}}.$

熵 H（以比特为单位）是在所有具有非零概率 w_i 的符号 a_i 上，每个符号的信息量的加权和

$H(A)=\sum _{w_{i}>0}w_{i}h(a_{i})=\sum _{w_{i}>0}w_{i}\log _{2}{1 \over w_{i}}=-\sum _{w_{i}>0}w_{i}\log _{2}{w_{i}}.$

(注意：概率为零的符号对熵没有贡献。当 w = 0 时，$w\log _{2}(1/w)=0\cdot \infty$ 是一个不定式；因此，根据洛必达法则

$\lim _{w\to 0^{+}}{\frac {\log _{2}{\frac {1}{w}}}{\frac {1}{w}}}=\lim _{w\to 0^{+}}{\frac {-{\frac {1}{w\ln 2}}}{-{\frac {1}{w^{2}}}}}=\lim _{w\to 0^{+}}{\frac {w}{\ln 2}}=0$.

为了简单起见，上述公式中省略了概率为零的符号。

根据香农信息论的信源编码定理，信息熵是给定字母表及其权重下，理论上可能的最小码字长度的度量。在这个例子中，加权平均码字长度为每个符号 2.25 比特，仅略大于计算出的每个符号 2.205 比特的信息熵。因此，此代码不仅在没有其他可行代码性能更好的意义上是最优的，而且它也非常接近香农确定的理论极限。

注意，一般来说，霍夫曼编码不一定是唯一的，但它始终是最小化 $L(C)$ 的代码之一。

基本技术

信源生成 4 个不同的符号 $\{a_{1},a_{2},a_{3},a_{4}\}$，其概率为 $\{0.4;0.35;0.2;0.05\}$。从左到右生成二叉树，取两个概率最小的符号，将它们合并在一起形成另一个等效符号，其概率等于两个符号的概率之和。重复此过程，直到只剩下一个符号。然后可以从右到左反向读取树，为不同的分支分配不同的位。最终的霍夫曼编码为

符号	代码
a1	0
a2	10
a3	110
111

用 2 位/符号来表示由 4 个符号组成的信号的标准方法，但信源的信息熵为 1.73 位/符号。如果使用此霍夫曼编码来表示信号，则平均长度将降低到 1.85 位/符号；它仍然远低于理论极限，因为符号的概率不同于 2 的负幂。

该技术通过创建节点的二叉树来实现。这些可以存储在常规数组中，数组的大小取决于符号的数量 $n$。节点可以是叶节点或内部节点。最初，所有节点都是叶节点，它们包含符号本身、权重（出现频率）和可选的指向父节点的链接，这使得从叶节点开始很容易反向读取代码。内部节点包含符号权重、指向两个子节点的链接和可选的指向父节点的链接。根据惯例，位 '0' 表示跟随左子节点，位 '1' 表示跟随右子节点。一个完整的树有 $n$ 个叶节点和 $n-1$ 个内部节点。

该过程基本上从叶节点开始，叶节点包含它们代表的符号的概率，然后创建一个新节点，其子节点是 2 个概率最小的节点，这样新节点的概率就等于子节点的概率之和。将之前的 2 个节点合并为一个节点（因此不再考虑它们），并考虑新节点，重复此过程，直到只剩下一个节点，即霍夫曼树。

最简单的构造算法使用优先队列，其中概率最低的节点具有最高优先级。

1. 为每个符号创建一个叶节点，并将其添加到优先队列中。
2. 当队列中有多个节点时
   1. 从队列中移除两个优先级最高（概率最低）的节点。
   2. 创建一个新的内部节点，将这两个节点作为子节点，并将概率设置为两个节点的概率之和。
   3. 将新节点添加到队列中。
3. 剩余的节点是根节点，树已经完成。

由于高效的优先队列数据结构每次插入需要 O(log n) 时间，并且具有 n 个叶节点的树有 2n−1 个节点，因此该算法在 O(n log n) 时间内运行。

如果符号按概率排序，则可以使用两个队列创建线性时间 (O(n)) 的霍夫曼树，第一个队列包含初始权重（以及指向相关叶节点的指针），组合权重（以及指向树的指针）被放入第二个队列的尾部。这确保了最低权重始终保留在两个队列的头部之一。

1. 从与符号数量相同的叶节点开始。
2. 将所有叶节点入队到第一个队列中（按概率升序，以便概率最低的项位于队列头部）。
3. 当队列中有多个节点时
   1. 通过检查两个队列的头部，将两个权重最低的节点出队。
   2. 创建一个新的内部节点，将这两个刚刚移除的节点作为子节点（任何节点都可以是任何子节点），并将它们的权重之和作为新权重。
   3. 将新节点入队到第二个队列的尾部。
4. 剩余的节点是根节点；树现在已经生成。

最小化码字长度的方差通常是有益的。例如，接收霍夫曼编码数据的通信缓冲区可能需要更大才能处理特别长的符号，如果树特别不平衡的话。为了最小化方差，只需通过选择第一个队列中的项来打破队列之间的联系。这种修改将保留霍夫曼编码的数学最优性，同时最小化方差和最长字符代码的长度。

主要属性

使用的概率可以是基于平均经验的应用程序域的通用概率，也可以是压缩文本中实际发现的频率。（这种变化要求将频率表或其他编码提示存储在压缩文本中；实现采用各种技巧来有效地存储表。）

当每个输入符号的概率都是 2 的负幂时，霍夫曼编码是最优的。前缀码在较小的字母表上往往效率略低，在这种情况下，概率通常落在这些最佳点之间。“阻塞”，或通过将多个符号合并成固定长度或可变长度的“词”来扩展字母表大小，然后进行霍夫曼编码，通常会有所帮助，尤其是在相邻符号相关联的情况下（如自然语言文本）。霍夫曼编码的最坏情况可能发生在符号的概率超过 2^-1 = 0.5 时，这使得效率的上限无界。这些情况通常对称为游程长度编码的阻塞形式有很好的反应。

算术编码比霍夫曼编码略有优势，但在实践中，这些优势很少大到足以抵消算术编码更高的计算复杂度和专利使用费。（截至 2006 年 7 月，IBM 在美国拥有许多算术编码方法的专利；请参阅关于算术编码的美国专利。）

变化

哈夫曼编码有很多变体，其中一些使用类似哈夫曼的算法，而另一些则找到最佳前缀码（例如，对输出施加不同的限制）。请注意，在后一种情况下，该方法不必类似哈夫曼，实际上也不必是多项式时间。一篇关于哈夫曼编码及其变体的论文列表，见“无损源编码的代码和解析树”[1].

n元哈夫曼编码

n元哈夫曼算法使用{0, 1, ... , n − 1}字母表来编码消息并构建一个n元树。这种方法在哈夫曼最初的论文中有所考虑。与二进制（n等于2）代码相同，只是n个概率最小的符号被组合在一起，而不是仅仅组合2个概率最小的符号。请注意，对于大于2的n，并非所有源词集都可以正确地为哈夫曼编码形成一个n元树。在这种情况下，必须添加额外的0概率占位符。这是因为树必须形成一个n到1的压缩器。对于二进制编码，这是一个2到1的压缩器：任何大小的集合都可以形成这样的压缩器。

自适应哈夫曼编码

一种称为自适应哈夫曼编码的变体根据源字符串中最近的实际频率动态计算概率。这与LZ算法家族有些相关。

哈夫曼模板算法

在哈夫曼编码的实现中，权重通常表示数值概率，但是上面给出的算法并不需要这个；它只需要一种对权重进行排序和加和的方法。哈夫曼模板算法允许使用任何类型的权重（成本、频率、权重对、非数值权重）以及许多组合方法之一（不仅仅是加法）。这样的算法可以解决其他最小化问题，例如最小化 $\max _{i}\left[w_{i}+\mathrm {length} \left(c_{i}\right)\right]$，这个问题最初应用于电路设计[2].

长度限制哈夫曼编码

长度限制哈夫曼编码是一种变体，其目标仍然是实现最小加权路径长度，但有一个额外的限制，即每个码字的长度必须小于给定的常数。包合并算法使用一种简单的贪婪方法解决这个问题，该方法与哈夫曼算法非常相似。其时间复杂度为 $O(nL)$，其中 $L$ 是码字的最大长度。与预排序和未排序的常规哈夫曼问题分别不同，没有已知的算法能够在线性或线性对数时间内解决这个问题。

不等字母成本的哈夫曼编码

在标准的哈夫曼编码问题中，假设构造码字的集合中的每个符号都有相同的传输成本：一个长度为N位的码字始终具有N的成本，无论其中有多少位是0，有多少位是1等等。在假设下，最小化消息的总成本和最小化数字的总数是相同的。

不等字母成本的哈夫曼编码是对这种假设不再成立的推广：由于传输介质的特性，编码字母的字母可能具有不均匀的长度。例如，莫尔斯码的编码字母表，其中一个“短划线”的发送时间比一个“点”更长，因此在传输时间中一个“短划线”的成本更高。目标仍然是最小化加权平均码字长度，但是仅最小化消息使用的符号数量已经不足够。没有已知的算法能够以与常规哈夫曼编码相同的方式或以相同效率解决这个问题。

最优字母二叉树（Hu-Tucker编码）

在标准的哈夫曼编码问题中，假设任何码字都可以对应于任何输入符号。在字母版本中，输入和输出的字母顺序必须相同。因此，例如，$A=\left\{a,b,c\right\}$ 不能分配代码 $H\left(A,C\right)=\left\{00,1,01\right\}$，而应该分配 $H\left(A,C\right)=\left\{00,01,1\right\}$ 或 $H\left(A,C\right)=\left\{0,10,11\right\}$。这也被称为Hu-Tucker问题，以发表了第一个线性对数解的论文作者命名，该解为这个最优二元字母问题，与哈夫曼算法有一些相似之处，但不是这个算法的变体。这些最优字母二叉树通常用作二叉搜索树。

规范哈夫曼码

如果与字母顺序输入对应的权重按数字顺序排列，则霍夫曼编码具有与最佳字母编码相同的长度，可以通过计算这些长度来找到最佳字母编码，从而使 Hu-Tucker 编码变得不必要。从数字上（重新）排序输入产生的代码有时被称为*规范霍夫曼代码*，并且由于编码/解码的简便性，它通常是实践中使用的代码。寻找这种代码的技术有时被称为**霍夫曼-香农-法诺编码**，因为它与霍夫曼编码一样最优，但重量概率按字母顺序排列，就像香农-法诺编码一样。与该示例对应的霍夫曼-香农-法诺代码是$\{000,001,01,10,11\}$，它与原始解具有相同的代码字长度，因此也是最优的。

应用

尽管算术编码提供的压缩性能优于霍夫曼编码，但霍夫曼编码由于其简单性、高速以及不受专利限制而仍然被广泛使用。

如今，霍夫曼编码通常用作其他一些压缩方法的“后端”。DEFLATE（PKZIP 的算法）和多媒体编解码器（如 JPEG 和 MP3）具有前端模型和量化，然后进行霍夫曼编码。

参考资料

• 霍夫曼的原始文章：D.A. 霍夫曼，“一种构造最小冗余码的方法”，《无线电工程师学会学报》，1952 年 9 月，第 1098-1102 页
• 背景故事：简介：David A. Huffman，《科学美国人》，1991 年 9 月，第 54-58 页
• Thomas H. Cormen、Charles E. Leiserson、Ronald L. Rivest 和 Clifford Stein。算法导论，第二版。麻省理工学院出版社和麦格劳-希尔出版社，2001 年。 ISBN 0-262-03293-7。第 16.3 节，第 385-392 页。

外部链接

• 用于解释霍夫曼编码过程的程序。
• N 叉霍夫曼模板算法
• Sloane A098950 最大高度霍夫曼树的最小 K 阶序列
• 在图灵机上计算霍夫曼编码
• Mordecai J. Golin、Claire Kenyon、Neal E. Young“具有不等字母成本的霍夫曼编码”（PDF），STOC 2002：785-791
• 霍夫曼编码：CS2 课程作业 这是一个很好的霍夫曼编码入门
• 关于生成霍夫曼树的快速教程
• 指向霍夫曼编码可视化的指针
• C 语言中的霍夫曼编码
• JavaScript 中的霍夫曼编码
• 霍夫曼二进制算法小程序
• 霍夫曼解码的实现方法
• Python 实现的描述