R 中的数据挖掘算法/聚类/期望最大化 (EM)

本章旨在概述由 (尽管该技术是在文献中非正式提出的，正如作者所建议的) 在 R-Project 环境中提出的期望最大化 (EM) 技术。第一部分介绍了代表性聚类和混合模型。第二部分将介绍算法细节和一个案例研究。

将使用的 R 包是 Chris Fraley 和 Adrian Raftery 开发的 MCLUST-v3.3.2，可在 CRAN 库中找到。MCLUST 工具是一个软件，它包括以下功能：正态混合建模 (EM)；通过分层聚类方法进行 EM 初始化；基于贝叶斯信息准则 (BIC) 估计聚类数量；以及显示，包括不确定性图和维投影。

本文档的信息来源分为两组：(i) R 和 MCLUST 的手册和指南，包括技术报告 ，它是该项目的参考基础，概述了 MCLUST，并提供了一些示例；(ii) 在文献中找到的理论论文、调查和书籍。

简介

聚类是指识别具有共同特征且彼此凝聚且分离的实体组。由于在不同知识领域中的多种应用，人们对聚类的兴趣日益浓厚。重点关注了在海量数据集中对客户和产品的分组搜索、Web 用法数据中的文档分析、来自微阵列的基因表达以及图像分析（其中聚类用于分割）。

聚类方法可以分为几类。一种广泛使用的方法是层次聚类，它最初认为每个点都代表一个组，并在每次迭代中合并两个组，以优化某些标准。一个流行的标准是 提出的，包括组内平方和之和，由组之间的最短距离给出（单链接方法）。

另一个典型的类别是基于迭代重定位的，其中数据在每次迭代中从一个组移动到另一个组。由于使用为每个聚类创建的模型，该模型总结了组元素的特征，因此也称为代表性聚类。该类别中最流行的方法是 K-Means，由 提出，该方法基于使用平方和标准的迭代重定位。

在统计学和优化问题中，通常需要最大化或最小化特定空间中的函数及其变量。由于这些优化问题可能假设多种不同类型，每种类型都有其自身的特征，因此已经开发了许多技术来解决它们。这些技术在数据挖掘和知识发现领域非常重要，因为它可以作为大多数复杂而强大的方法的基础。

其中一项技术是 最大似然，其主要目标是使用特定数据集调整统计模型，估计其未知参数，以便函数可以描述数据集中的所有参数。换句话说，该方法将使用数据集或已知分布从统计模型中调整一些变量，以便模型可以“描述”每个数据样本并估计其他数据样本。

人们意识到聚类可以基于概率模型来覆盖缺失值。这提供了有关数据应何时符合模型的见解，并已导致开发新的聚类方法，例如期望最大化 (EM)，该方法基于有限混合模型中未观察变量的最大似然原理。

讨论的技术

EM 算法是一种无监督的聚类方法，即不需要训练阶段，基于混合模型。它遵循一种迭代方法，次优，试图找到其属性具有最大似然的概率分布的参数。

一般来说，算法的输入是数据集 (x)，聚类总数 (M)，接受的收敛误差 (e) 和最大迭代次数。对于每次迭代，首先执行 E-Step (Expectation)，它估计每个点属于每个聚类的概率，然后执行 M-Step (Maximization)，它重新估计每个类的概率分布的参数向量。当分布参数收敛或达到最大迭代次数时，算法结束。

算法

初始化

M 个类（或聚类）中的每个类 j 都由一个参数向量 (θ) 组成，该向量由均值 ($\mu _{j}$) 和协方差矩阵 ($P_{j}$) 组成，它代表用于表征观察到的和未观察到的数据集 x 实体的高斯概率分布（正态）的特征。

$\theta (t)=(\mu _{j}(t),\ P_{j}(t)),\ j\ =\ 1,...,M$

在初始时刻 (t = 0) ，实现可以随机生成均值（$\mu _{j}$）和协方差矩阵（$P_{j}$）的初始值。EM 算法旨在逼近真实分布的参数向量 (θ)。MCLUST 提供的另一种选择是用层次聚类技术获得的聚类来初始化 EM。

E 步

这一步负责估计每个元素属于每个聚类的概率（$P(C_{j}|x_{k})$）。每个元素都由一个属性向量组成（$x_{k}$）。每个聚类中点的相关程度由每个元素属性的可能性与其在聚类 $C_{j}$ 中其他元素的属性的比较给出。

$P(C_{j}|x)={\frac {|\sum _{j}(t)|^{-{\frac {1}{2}}}\ e^{n_{j}}\ P_{j}(t)}{\sum _{k=1}^{M}\ |\sum _{j}(t)|^{-{\frac {1}{2}}}\ e^{n_{j}}\ P_{k}(t)}}}$

M 步

这一步负责估计每类概率分布的参数，以便进行下一步操作。首先计算通过所有点在每个点相关程度函数上的平均值获得的类别 j 的均值（μj）。

$\mu _{j}(t+1)={\frac {\sum _{k=1}^{N}\ P(C_{j}|x_{k})\ x_{k}}{\sum _{k=1}^{N}\ P(C_{j}|x_{k})}}$

为了计算下一个迭代的协方差矩阵，应用贝叶斯定理，这意味着 $P(A|B)=(P(B|A)*P(A))/P(B)$，基于类发生条件概率。

$\sum _{j}(t+1)={\frac {\sum _{k=1}^{N}\ P(C_{j}|x_{k})\ (x_{k}-\mu _{j}(t))\ (x_{k}-\mu _{j}(t))}{\sum _{k=1}^{N}\ P(C_{j}|x_{k})}}$

每个类的出现概率是通过概率的平均值计算的（$C_{j}$）作为每个点从类的相关度函数。

$P_{j}(t+1)={\frac {1}{N}}\sum _{k=1}^{N}P(C_{j}|x_{k})$

属性表示参数向量 θ，它表征每个类的概率分布，将在下一次算法迭代中使用。

收敛测试

在每次迭代执行后，将进行收敛测试，以验证迭代的属性向量与前一次迭代的属性向量之间的差异是否小于参数给定的可接受误差容限。一些实现使用类分布平均值之间的差异作为收敛标准。

if(||θ(t + 1) − θ(t)|| < ǫ)
   stop
else
   call E-Step
end

该算法具有在每一步估计具有最大局部似然性的新属性向量的特性，但不一定是全局的，这降低了它的复杂性。但是，根据数据的离散程度和数据量，算法可能会因为定义的最大迭代次数而停止。

实施

包

R 中的期望最大化算法， 在 中提出，将使用 mclust 包。此包包含执行聚类算法的关键方法，包括用于 E 步和 M 步计算的函数。包手册解释了其所有函数，包括简单的示例。此手册可在 中找到。

mclust 包还为 EM 提供了各种模型，也为层次聚类 (HC) 提供了模型，它由协方差结构定义。这些模型在表 1 中列出，并在 中详细解释。

表 1：协方差矩阵结构。

标识符	模型	HC	EM	分布	体积	形状	方向
E		*	*	(单变量)	相等
V		*	*	(单变量)	可变
EII	$\lambda I$	*	*	球形	相等	相等	NA
VII	$\lambda _{k}I$	*	*	球形	可变	相等	NA
EEI	$\lambda A$		*	对角线	相等	相等	坐标轴
VEI	$\lambda _{k}A$		*	对角线	可变	相等	坐标轴
EVI	$\lambda A_{k}$		*	对角线	相等	可变	坐标轴
VVI	$\lambda _{k}A_{k}$		*	对角线	可变	可变	坐标轴
EEE	$\lambda DAD^{T}$	*	*	椭圆形	相等	相等	相等
EEV	$\lambda D_{k}AD_{k}^{T}$		*	椭圆形	相等	相等	可变
VEV	$\lambda _{k}D_{k}AD_{k}^{T}$		*	椭圆形	可变	相等	可变
VVV	$\lambda _{k}D_{k}A_{k}D_{k}^{T}$	*	*	椭圆形	可变	可变	可变

执行算法

函数“em”可用于执行期望最大化方法，因为它实现了参数化高斯混合模型（GMM）的该方法，从E步开始。该函数使用以下参数

• 模型名称：所用模型的名称；

• 数据：所有收集的数据，必须都是数值型。如果数据格式用矩阵表示，则行表示样本（观测值），列表示变量；

• 参数：模型参数，可以取以下值：pro、mean、variance 和 Vinv，分别对应于混合的各个组成部分的混合比例、每个组成部分的均值、参数方差和数据区域的估计超体积。

• 其他：与主题无关的参数，此处不作描述。更多详细信息可以在包手册中找到。

执行完后，函数将返回

• 模型名称：模型名称；
• z：一个矩阵，其在位置[I,k]的元素表示第i个样本属于第k个混合分量的条件概率；
• 参数：与输入相同；
• 其他：其他指标，此处不作讨论。更多详细信息可以在包手册中找到。

一个简单的例子

为了演示如何使用R来执行期望最大化方法，以下算法提供了一个测试数据集的简单示例。该示例也可以在包手册中找到。

> modelName = ``EEE''
> data = iris[,-5]
> z = unmap(iris[,5])
> msEst <- mstep(modelName, data, z)
> names(msEst)
> modelName = msEst$modelName
> parameters = msEst$parameters
> em(modelName, data, parameters)

第一行执行M步，以便生成在em函数中使用的参数。该函数称为mstep，其输入是模型名称，如“EEE”，数据集为iris数据集，最后是z矩阵，该矩阵包含每个类包含每个数据样本的条件概率。该z矩阵由unmap函数生成。

执行完M步后，算法将显示（第2行）此函数返回的对象的属性。第三行将使用M步方法的一些结果作为输入开始聚类过程。

聚类方法将返回在该过程中估计的参数以及每个样本落入每个类的条件概率。这些参数包括均值和方差，最后一个对应于使用mclustVariance方法。

查看

本节将介绍MCLUST包中提供的一些可视化示例。首先将展示一个从选择簇数、初始化和分区等方面展示聚类整体过程的简单示例。然后将解释一个使用两个随机混合与两个高斯混合进行比较的教学示例。

基本示例

这是一个简单的示例，用于展示MCLUST包提供的功能。它应用于faithful数据集（包含在R项目中）。首先，聚类分析估计最能代表该数据集的簇数以及点扩散的协方差结构。这是通过称为贝叶斯信息准则（BIC）的技术来执行的，该技术将簇数从1变为9。BIC是最大化对数似然的值，用模型中参数数量的惩罚来衡量。然后执行层次聚类技术（HC），该技术不需要初始化阶段。HC的输出，即每个元素所属的簇，被用来初始化期望最大化技术（EM）。执行完EM聚类后，将在下面显示图表

### basic_example.R ###
# usage: R --no-save < basic_example.R

library(mclust)           # load mclust library
x = faithful[,1]          # get the first column of the faithful data set
y = faithful[,2]          # get the second column of the faithful data set
plot(x,y)                 # plot the spread points before the clustering
model <- Mclust(faithful) # estimate the number of cluster (BIC), initialize (HC) and clusterize (EM)
data = faithful           # get the data set 
plot(model, faithful)     # plot the clustering results

文件:Basic points.pdf

教学示例

为了展示两种不同的场景，开发了一个教学示例：（a）模型不代表数据；（b）数据符合模型。本示例旨在展示EM在带噪声和干净的数据集中是如何工作的。

a) 均匀随机混合

通过一个均匀随机函数生成一个带噪声的数据集。点的扩散在图表中显示。然后使用默认参数执行聚类分析（即将簇数从1变为9）。聚类工具显示一条警告消息，提示最佳模型出现在最小值或最大值处，在本例中，所有点都被分组到一个簇中，因此是最小值。

### random_example.R ###
# usage: R --no-save < random_example.R

library(mclust)                  # load mclust library
x1 = runif(20)                   # generate 20 random random numbers for x axis (1st class)
y1 = runif(20)                   # generate 20 random random numbers for y axis (1st class)
x2 = runif(20)                   # generate 20 random random numbers for x axis (2nd class)
y2 = runif(20)                   # generate 20 random random numbers for y axis (2nd class)
rx = range(x1,x2)                # get the axis x range
ry = range(y1,y2)                # get the axis y range
plot(x1, y1, xlim=rx, ylim=ry)   # plot the first class points
points(x2, y2 )                  # plot the second class points
mix = matrix(nrow=40, ncol=2)    # create a dataframe matrix 
mix[,1] = c(x1, x2)              # insert first class points into the matrix
mix[,2] = c(y1, y2)              # insert second class points into the matrix
mixclust = Mclust(mix)           # initialize EM with hierarchical clustering, execute BIC and EM

# Warning messages:
# 1: In summary.mclustBIC(Bic, data, G = G, modelNames = modelNames) :
#    best model occurs at the min or max # of components considered
# 2: In Mclust(mix) : optimal number of clusters occurs at min choice

b) 两个高斯混合

此场景由两个通过高斯分布函数（正态分布）生成并分离良好的数据集组成。点在第一个图表中显示。应用了EM聚类，结果也显示在下面的图表中。正如我们所看到的，EM聚类获得了两个符合数据的符合数据的两个高斯模型。

### gaussian_example.R ###
# usage: R --no-save < gaussian_example.R

library(mclust)                  # load mclust library
x1 = rnorm(n=20, mean=1, sd=1)   # get 20 normal distributed points for x axis with mean=1 and std=1 (1st class)
y1 = rnorm(n=20, mean=1, sd=1)   # get 20 normal distributed points for x axis with mean=1 and std=1 (2nd class)
x2 = rnorm(n=20, mean=5, sd=1)   # get 20 normal distributed points for x axis with mean=5 and std=1 (1st class)
y2 = rnorm(n=20, mean=5, sd=1)   # get 20 normal distributed points for x axis with mean=5 and std=1 (2nd class)
rx = range(x1,x2)                # get the axis x range
ry = range(y1,y2)                # get the axis y range
plot(x1, y1, xlim=rx, ylim=ry)   # plot the first class points
points(x2, y2)                   # plot the second class points
mix = matrix(nrow=40, ncol=2)    # create a dataframe matrix 
mix[,1] = c(x1, x2)              # insert first class points into the matrix
mix[,2] = c(y1, y2)              # insert second class points into the matrix
mixclust = Mclust(mix)           # initialize EM with hierarchical clustering, execute BIC and EM
plot(mixclust, data = mix)       # plot the two distinct clusters found

文件:Gaussian density.pdf 文件:Gaussian uncertainty.pdf

案例研究

场景

要分析的场景由MCLUST包中名为“wreath”的样本数据集组成。进行更详细的聚类分析，应用于由14个点组成的场景，超过了默认MCLUST参数允许的最大簇数。聚类技术执行两次：（i）第一次基于默认MCLUST；（ii）使用自定义参数。

输入数据

该案例研究的输入是 MCLUST 包提供的 wreath 数据集。该数据集包含 14 个点组，如下图所示，可以使用球形或椭圆形对其进行建模，考虑到数据旋转导致的取向。

### case_input.R ###
# usage: R --no-save < case_default.R

plot(wreath[,1],wreath[,2])

执行

聚类执行了两次。第一次基于 MCLUST 工具提供的默认参数，将聚类数量从 1 变化到 9，这比拟合案例研究数据集所需的聚类数量要少。聚类数量的估计显示在一个图表中，该图表改变聚类数量并计算每个值的贝叶斯信息准则 (BIC)。我们可以看到，使用默认参数的 BIC 是发散的，而预期是找到一个峰值，然后下降，表明最佳的聚类数量。

### case_default.R ###
# usage: R --no-save < case_default.R

library(mclust)

wreathBIC <- mclustBIC(wreath)
plot(wreathBIC, legendArgs = list(x = "topleft"))

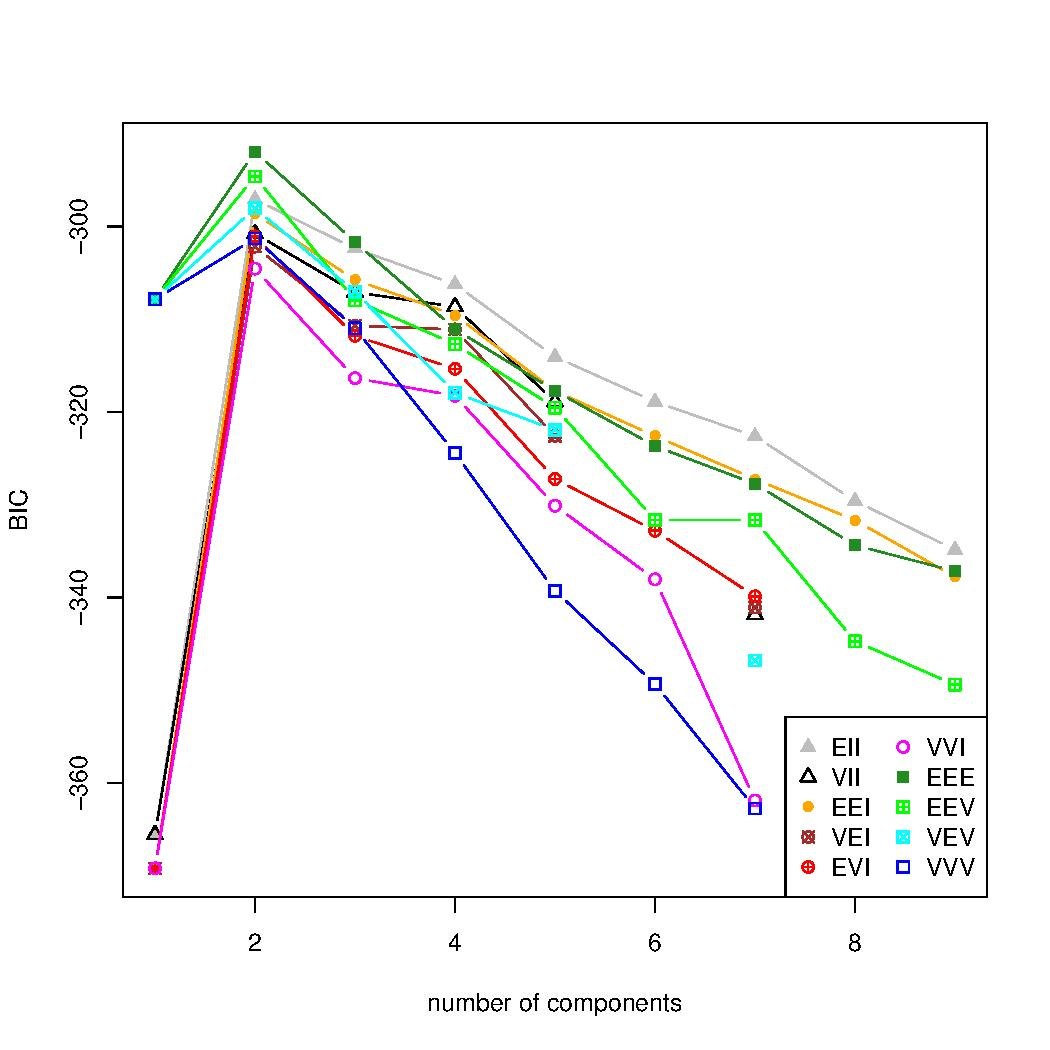
然后，聚类数量被定制，修改为从 1 变化到 20，如下所示。BIC 技术将给出最佳的聚类数量，在本例中为 14 个聚类，以及具有该数据集属性的系数结构，即 EEV，这意味着聚类具有相似的形状、相似的体积，但不同的方向。再次执行 BIC 方法后，我们可以看到，由图表中的峰值指示的 14 个聚类，是呈现该数据最大似然性的聚类数量。

### case_customized.R ###
# usage: R --no-save < case_customized.R

library(mclust)
wreathDefault <- mclustBIC(wreath)
wreathCustomize <- mclustBIC(wreath, G = 1:20, x = wreathDefault)
plot(wreathCustomize, G = 10:20, legendArgs = list(x = "bottomleft"))
summary(wreathCustomize, wreath)

输出

该聚类的输出使用下图中所示的 mclust2Dplot 方法进行分析。使用了密度可视化。找到的聚类以 14 个模型为特征，这些模型具有椭圆体的分布，方向不同，与数据一致。方法摘要可以稍后执行，以分析聚类结果的其他方面。

### case_output.R ###
# usage: R --no-save < case_customized.R

library(mclust)
data(wreath)
wreathBIC <- mclustBIC(wreath)
wreathBIC <- mclustBIC(wreath, G = 1:20, x = wreathBIC)
wreathModel <- summary(wreathBIC, data = wreath)
mclust2Dplot(data = wreath, what = "density", identify = TRUE, parameters = wreathModel$parameters, z = wreathModel$z)

分析

我们可以看到，创建用来表示点的混合模型与数据集相符。在本例中，各组之间没有交集，因此所有点都被正确分类。聚类方向允许该方法找到更好的椭圆形来表示这些点。

我们得出结论，尽管依赖于聚类数量和初始化阶段，EM 聚类技术仍然是一种有效的方法，可以为多种数据分散场景产生良好的结果。使用 BIC 估计聚类数量，以及使用层次聚类 (HC)（不依赖于聚类数量）初始化聚类，可以提高结果的质量。