简介

聚类是一种无监督机器学习算法，它将数据集中的实体分组，这些实体在同一个簇中具有高度相似性。如今，许多领域都在使用这些类型的算法以自动化的方式将数据集分成组，并且仍然可以获得高质量的结果。

聚类过程不是一个通用的过程，因为存在许多组数据集，对于其中的一些数据集，使用的度量类型是相关的，而对于其他数据集，代表每个簇的实体更有趣。与数据集组类似，存在许多聚类算法，每个算法都试图利用数据类型，因此，它们中的每一个都更适合特定类型的数据。

本节将更详细地解释围绕中心点划分 (PAM) 算法，展示算法的工作原理、参数以及含义、数据集示例、如何执行算法以及使用数据集作为输入的执行结果。

围绕中心点划分 (PAM) 算法

算法

PAM 算法由 Leonard Kaufman 和 Peter J. Rousseeuw 开发，该算法与 K 均值非常相似，主要是因为两者都是划分算法，换句话说，两者都将数据集分成组（簇），并且两者都试图最小化误差，但 PAM 使用中心点，中心点是代表其插入的组的数据集中的实体，而 K 均值使用中心点，中心点是人工创建的代表其簇的实体。

PAM 算法将包含 n 个对象的数据集分成 k 个簇，其中数据集和 k 都作为算法的输入。该算法使用不相似矩阵，其目标是最小化每个簇的代表与其成员之间的总体不相似性。该算法使用以下模型来解决问题： $F(x)={\text{minimize}}\sum _{i=1}^{n}\sum _{j=1}^{n}d(i,j)z_{ij}$

受制于

${\begin{array}{lll}\sum _{i=1}^{n}z_{ij}=1,j=1,2,..,n\\z_{ij}\leq y_{i},i,j=1,2,..,n\\\sum _{i=1}^{n}y_{i}=k,k={\text{number of clusters}}\\y_{i},z_{ij}\in \{0,1\},i,j=1,2,..,n\end{array}}$

其中 F(x) 是要最小化的主要函数，d(i,j) 是实体 i 和 j 之间的不相似性度量，而 z_ij 是一个确保仅计算来自同一簇的实体之间的不相似性的变量。其他表达式是约束条件，它们具有以下功能：(1.) 确保每个实体都分配给一个且仅一个簇，(2.) 确保实体分配给代表该簇的中心点，(3.) 确保恰好有 k 个簇，以及 (4.) 允许决策变量仅取 0 或 1 的值。

PAM 算法可以处理两种类型的输入，第一个是代表每个实体及其变量值的矩阵，第二个是直接的不相似矩阵，在后一种情况下，用户可以直接提供不相似性作为算法的输入，而不是代表实体的数据矩阵。无论哪种方式，该算法都能够找到问题的解决方案，在一般的分析中，该算法按照以下方式进行

构建阶段

1. 选择 k 个实体作为中心点，或者如果这些实体已提供，则将它们用作中心点；

2. 如果未提供，则计算不相似矩阵；

3. 将每个实体分配到其最近的中心点；

交换阶段

4. 对于每个簇，搜索该簇中的任何实体是否可以降低平均不相似系数，如果可以，则选择最能降低该系数的实体作为该簇的中心点；

5. 如果至少一个中心点已更改，则转到 (3)，否则结束算法。

实现

这并没有描述“PAM”算法。这是一种使用中心点的 K 均值变体，而不是具有其特征构建和交换阶段的 PAM。

PAM 算法的伪代码如下所示

算法 1：PAM 算法 输入： E = {e1,e2,...en}（要聚类的数据集或不相似矩阵）

k（簇的数量）

度量（在不相似矩阵上使用的度量类型）

diss（指示 E 是否是不相似矩阵的标志）

输出： M = {m1,m2,...,mk}（簇中心点的向量）

L = {l(e) | e = 1,2,...,n}（E 的簇标签集）

foreach m_i € M do

m_i ← e_j € E;（例如，随机选择）

end if diss ≠ true

不相似性 ← 计算不相似矩阵(E, 度量)；

else

不相似性 ← E；

end repeat

foreach e_i € E do

l(e_i) ← argminDissimilarity(e_i, 不相似性, M)；

end

已更改 ← false；

foreach m_i € M do

Mtmp ← 选择最佳簇中心点(E, 不相似性, L)；

end

if Mtmp ≠ M

M ← Mtmp；

已更改 ← true；

end

until 已更改 = true；

在 R 编程语言中，PAM 算法在 cluster 包中可用，可以通过以下命令调用

pam(x, k, diss, metric, medoids, stand, cluster.only, do.swap, keep.diss, keep.data,
trace.lev)

其中参数为

x：代表数据集实体的数值数据矩阵，或者可以是不相似矩阵，它取决于 diss 参数的值。如果 x 是数据矩阵，则每行都是一个实体，每列都是一个变量，在这种情况下，只要每对实体至少有一个不缺失的情况，就可以允许缺失值。如果 x 是不相似矩阵，则不允许缺失值。

k：数据集将被划分的簇的数量，其中 0 < k < n，其中 n 是实体的数量。

diss：逻辑标志，如果它是 TRUE，则 x 被用作不相似矩阵，如果它是 FALSE，则 x 将被视为数据矩阵。

度量：一个字符串，指定将使用两个度量标准中的每一个来计算不相似矩阵，度量变量可以是“欧几里得”以使用欧几里得距离，也可以是“曼哈顿”以使用曼哈顿距离。

stand：逻辑标志，如果它是 TRUE，则在计算不相似性之前对 x 中的测量值进行标准化。通过减去列的平均值并除以变量的平均绝对偏差，对每列进行标准化测量。如果 x 是不相似矩阵，则忽略此参数。

cluster.only：逻辑标志，如果它是 TRUE，则仅计算并返回聚类。

do.swap：逻辑标志，指示是否应执行交换阶段 (TRUE) 还是不执行 (FALSE)。

keep.diss: 逻辑标志，指示是否在结果中保留差异（TRUE）或不保留（FALSE）。

keep.data: 逻辑标志，指示是否在结果中保留输入数据 x（TRUE）或不保留（FALSE）。

trace.lev: 一个数值参数，指定在算法的构建和交换阶段打印诊断信息的跟踪级别。默认值为 0，不打印任何内容。

PAM 算法返回一个 pam 对象，其中包含有关算法执行结果的信息。

可视化

在 R 中，有两种方法可以查看 PAM 算法的结果：第一种方法是打印算法返回的对象，第二种方法是绘制对象中的数据，创建一个结果图形。第一种可视化信息的方法理解起来稍微复杂一些，但它提供了更完整和准确的信息，而第二种方法则容易理解得多，让用户能够更好地查看信息并添加对他而言相关的其他信息。

要以文本方式查看 PAM 算法执行结果的数据，有两种方法：一种比较简单，提供有关对象的更简洁的信息；另一种更详细，提供更完整的信息。在下面列出的两个命令中，第一个命令以简洁的方式打印信息，而第二个命令则以更完整的方式打印信息。

print (result)
summary (result)

可视化算法执行结果数据的另一种方法是使用图形，可以通过以下命令来实现。

plot (result)

示例：为了展示算法的使用示例及其执行结果，使用了一个包含少量实体和维度的简单数据集，如以下表格所示。

表 1：简单数据集

对象	属性 x	属性 y
1	1	1
2	2	3
3	1	2
4	2	2
5	10	4
6	11	5
7	10	6
8	12	5
9	11	6

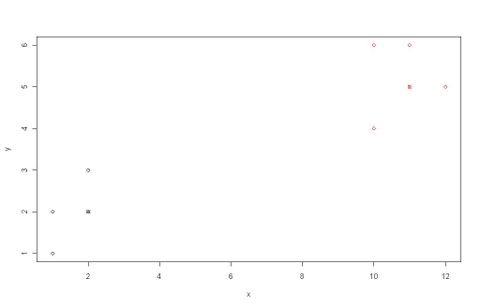
正如我们所见，数据被分成两个聚类，因此我们将使用 k = 2。PAM 算法可以按以下方式执行。

#load the table from a file
x <- read.table(“table.txt”)

#execute the pam algorithm with the dataset created for the example
result <- pam(x, 2, FALSE, "euclidean")

#print the results data in the screen
summary(result)

#plot a graphic showing the clusters and the medoids of each cluster
plot(result$data, col = result$clustering)
points(result$medoids, col = 1:2, pch = 4)

打印执行结果将得到

Medoids:
 ID  x y
4  4  2 2
6  6 11 5
Clustering vector:
1 2 3 4 5 6 7 8 9 
1 1 1 1 2 2 2 2 2 
Objective function:
  build     swap 
1.255618 0.915849 

Numerical information per cluster:
    size max_diss   av_diss diameter separation
[1,]    4 1.414214 0.8535534 2.236068   8.062258
[2,]    5 1.414214 0.9656854 2.236068   8.062258

Isolated clusters:
 L-clusters: character(0)
 L*-clusters: [1] 1 2

Silhouette plot information:
 cluster neighbor sil_width
3       1        2 0.8898942
4       1        2 0.8788422
1       1        2 0.8549629
2       1        2 0.8297000
6       2        1 0.8790384
9       2        1 0.8631441
8       2        1 0.8425790
7       2        1 0.8232848
5       2        1 0.7747713
Average silhouette width per cluster:
[1] 0.8633498 0.8365635
Average silhouette width of total data set:
[1] 0.8484685

36 dissimilarities, summarized :
  Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
1.0000  1.4142  8.3951  6.1559  9.9362 11.7050 
Metric :  euclidean 
Number of objects : 9

Available components:
 [1] "medoids"    "id.med"     "clustering" "objective"  "isolation"  "clusinfo"
   "silinfo"    "diss"       "call"      
[10] "data"

而绘制将得到

案例研究

在本节中，我们将使用 PAM 来进行案例研究。

场景

在本案例研究中，我们使用了 R 包 datasets 中提供的 iris 数据库的一部分。这个著名的（费舍尔或安德森）虹膜数据集给出了 3 个虹膜种类的 50 朵花的萼片长度和宽度以及花瓣长度和宽度的测量值（单位为厘米）。这 3 个种类分别是山鸢尾（Iris setosa）、变色鸢尾（versicolor）和维吉尼亚鸢尾（virginica）。利用此数据集提供的数据，很自然地会想到验证三种虹膜的每一种花的其他同类花是否真的相似。因此，在本案例研究中，我们将使用萼片和花瓣的长度和宽度将数据集聚类成 3 组，然后验证这些聚类是否真的与花卉种类相匹配。

在本案例研究中使用的数据集包含以下列

Flower: 花的 ID；
Sepal.Length: 萼片长度的数值（单位为厘米）；
Sepal.Width: 萼片宽度的数值（单位为厘米）；
Petal.Length: 花瓣长度的数值（单位为厘米）；
Petal.Width: 花瓣宽度的数值（单位为厘米）；
Species: 用于识别花的种类。

输入数据

输入数据是一个表格，包含原始 iris 数据集的 50%（75 个实体），原始数据集包含 150 朵花，每个花有 5 个属性。因此，在本案例研究中使用的数据集由以下表格表示。

表 2：从 iris 数据集中抽取的样本

Flower	Sepal.Length	Sepal.Width	Petal.Length	Petal.Width	Species
1	5.1	3.5	1.4	0.2	setosa
2	4.9	3.0	1.4	0.2	setosa
3	4.7	3.2	1.3	0.2	setosa
4	4.6	3.1	1.5	0.2	setosa
5	5.0	3.6	1.4	0.2	setosa
6	5.4	3.9	1.7	0.4	setosa
7	4.6	3.4	1.4	0.3	setosa
8	5.0	3.4	1.5	0.2	setosa
9	4.4	2.9	1.4	0.2	setosa
10	4.9	3.1	1.5	0.1	setosa
11	5.4	3.7	1.5	0.2	setosa
12	4.8	3.4	1.6	0.2	setosa
13	4.8	3.0	1.4	0.1	setosa
14	4.3	3.0	1.1	0.1	setosa
15	5.8	4.0	1.2	0.2	setosa
16	5.7	4.4	1.5	0.4	setosa
17	5.4	3.9	1.3	0.4	setosa
18	5.1	3.5	1.4	0.3	setosa
19	5.7	3.8	1.7	0.3	setosa
20	5.1	3.8	1.5	0.3	setosa
21	5.4	3.4	1.7	0.2	setosa
22	5.1	3.7	1.5	0.4	setosa
23	4.6	3.6	1.0	0.2	setosa
24	5.1	3.3	1.7	0.5	setosa
25	4.8	3.4	1.9	0.2	setosa
51	7.0	3.2	4.7	1.4	versicolor
52	6.4	3.2	4.5	1.5	versicolor
53	6.9	3.1	4.9	1.5	versicolor
54	5.5	2.3	4.0	1.3	versicolor
55	6.5	2.8	4.6	1.5	versicolor
56	5.7	2.8	4.5	1.3	versicolor
57	6.3	3.3	4.7	1.6	versicolor
58	4.9	2.4	3.3	1.0	versicolor
59	6.6	2.9	4.6	1.3	versicolor
60	5.2	2.7	3.9	1.4	versicolor
61	5.0	2.0	3.5	1.0	versicolor
62	5.9	3.0	4.2	1.5	versicolor
63	6.0	2.2	4.0	1.0	versicolor
64	6.1	2.9	4.7	1.4	versicolor
65	5.6	2.9	3.6	1.3	versicolor
66	6.7	3.1	4.4	1.4	versicolor
67	5.6	3.0	4.5	1.5	versicolor
68	5.8	2.7	4.1	1.0	versicolor
69	6.2	2.2	4.5	1.5	versicolor
70	5.6	2.5	3.9	1.1	versicolor
71	5.9	3.2	4.8	1.8	versicolor
72	6.1	2.8	4.0	1.3	versicolor
73	6.3	2.5	4.9	1.5	versicolor
74	6.1	2.8	4.7	1.2	versicolor
75	6.4	2.9	4.3	1.3	versicolor
101	6.3	3.3	6.0	2.5	virginica
102	5.8	2.7	5.1	1.9	virginica
103	7.1	3.0	5.9	2.1	virginica
104	6.3	2.9	5.6	1.8	virginica
105	6.5	3.0	5.8	2.2	virginica
106	7.6	3.0	6.6	2.1	virginica
107	4.9	2.5	4.5	1.7	virginica
108	7.3	2.9	6.3	1.8	virginica
109	6.7	2.5	5.8	1.8	virginica
110	7.2	3.6	6.1	2.5	virginica
111	6.5	3.2	5.1	2.0	virginica
112	6.4	2.7	5.3	1.9	virginica
113	6.8	3.0	5.5	2.1	virginica
114	5.7	2.5	5.0	2.0	virginica
115	5.8	2.8	5.1	2.4	virginica
116	6.4	3.2	5.3	2.3	virginica
117	6.5	3.0	5.5	1.8	virginica
118	7.7	3.8	6.7	2.2	virginica
119	7.7	2.6	6.9	2.3	virginica
120	6.0	2.2	5.0	1.5	virginica
121	6.9	3.2	5.7	2.3	virginica
122	5.6	2.8	4.9	2.0	virginica
123	7.7	2.8	6.7	2.0	virginica
124	6.3	2.7	4.9	1.8	virginica
125	6.7	3.3	5.7	2.1	virginica

执行

该过程按以下步骤进行

#import data
data <- read.table(“sampleiris.txt”)

#execution
result <- pam(data[1:4], 3, FALSE, “euclidean”)

#print results
summary(result)

#plot clusters
plot (data, col = result$clustering)
#add the medoids to the plot
points(result$medoids, col = 1:3, pch = 4)

输出

执行结果中打印了以下数据。

Medoids:
    ID Sepal.Length Sepal.Width Petal.Length Petal.Width
8    8          5.0         3.4          1.5         0.2
64  39          6.1         2.9          4.7         1.4
103 53          7.1         3.0          5.9         2.1
Clustering vector:
  1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20  21  22
  23  24  25  51  52  53  54  55  56 
  1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1
   1   1   1   2   2   2   2   2   2 
 57  58  59  60  61  62  63  64  65  66  67  68  69  70  71  72  73  74  75 101 102 103
 104 105 106 107 108 109 110 111 112 
  2   2   2   2   2   2   2   2   2   2   2   2   2   2   2   2   2   2   2   3   2   3
   3   3   3   2   3   3   3   2   2 
113 114 115 116 117 118 119 120 121 122 123 124 125 
  3   2   2   3   3   3   3   2   3   2   3   2   3 
Objective function:
    build      swap 
0.7148339 0.6990539 

Numerical information per cluster:
     size max_diss   av_diss diameter separation
[1,]   25 1.236932 0.5137400 2.042058  1.9000000
[2,]   34 1.951922 0.8085343 2.727636  0.3741657
[3,]   16 1.284523 0.7559609 2.147091  0.3741657 

Isolated clusters:
 L-clusters: [1] 1
 L*-clusters: character(0)

Silhouette plot information:
    cluster neighbor   sil_width
1         1        2  0.84941732
5         1        2  0.84830238
8         1        2  0.84812593
18        1        2  0.84784555
12        1        2  0.83221128
22        1        2  0.82890349
20        1        2  0.82456328
3         1        2  0.82337894
7         1        2  0.81910409
10        1        2  0.81662688
11        1        2  0.80769429
2         1        2  0.80592613
13        1        2  0.80278163
4         1        2  0.79810574
23        1        2  0.79482977
24        1        2  0.78999596
17        1        2  0.78539723
21        1        2  0.78454015
25        1        2  0.77452963
6         1        2  0.75995941
9         1        2  0.74605493
14        1        2  0.74277337
19        1        2  0.72082914
15        1        2  0.71581750
16        1        2  0.66155611
68        2        3  0.60036142
56        2        3  0.59753885
62        2        3  0.59698924
72        2        3  0.59691421
70        2        3  0.59514179
54        2        3  0.58507022
67        2        3  0.56989428
60        2        1  0.56350914
63        2        3  0.55592514
75        2        3  0.54720666
74        2        3  0.53971473
64        2        3  0.53757677
69        2        3  0.51098390
65        2        1  0.50762488
107       2        3  0.48295375
55        2        3  0.46851074
52        2        3  0.46827948
59        2        3  0.44164146
66        2        3  0.42147865
71        2        3  0.41421605
73        2        3  0.41282512
122       2        3  0.40891392
120       2        3  0.40207904
57        2        3  0.39510378
114       2        3  0.37176468
124       2        3  0.34854822
102       2        3  0.33532624
61        2        1  0.32662688
58        2        1  0.20142024
51        2        3  0.19024422
115       2        3  0.16320750
53        2        3  0.11554863
112       2        3 -0.07433144
111       2        3 -0.07748205
103       3        2  0.59622203
106       3        2  0.59241159
108       3        2  0.58027197
110       3        2  0.56716967
123       3        2  0.56182697
121       3        2  0.55568135
119       3        2  0.53242285
118       3        2  0.52551154
125       3        2  0.51206488
105       3        2  0.49243542
101       3        2  0.45749953
113       3        2  0.44409513
109       3        2  0.37181492
117       3        2  0.26375026
116       3        2  0.21777715
104       3        2  0.21412781
Average silhouette width per cluster:
[1] 0.7931708 0.4153331 0.4678177
Average silhouette width of total data set:
[1] 0.5524757

2775 dissimilarities, summarized :
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 0.1000  1.1136  2.5080  2.6329  3.9006  7.0852 
Metric :  euclidean 
Number of objects : 75

Available components:
 [1] "medoids"    "id.med"     "clustering" "objective"  "isolation"  "clusinfo"
   "silinfo"    "diss"       "call"      
[10] "data"

同时生成了以下图形。

分析

在执行算法并分析数据后，我们可以得出结论：聚类分组良好，与每朵花的种类相关。数据中共有 75 个元素，25 个属于Setosa 种类，25 个属于Versicolor 种类，25 个属于Virginica 种类，算法将Setosa 的元素聚类为集群 1，将Versicolor 的元素聚类为集群 2，将Virginica 的元素聚类为集群 3。在验证结果后，我们发现 75 个元素中，有 66 个被正确地聚类，误差率为 12%——这是一个非常好的结果。

参考文献

R 开发核心团队，R：一种统计计算语言和环境。
Kaufman, L., Rousseeuw, P. J., 中位数聚类。