R 中的数据挖掘算法/频繁模式挖掘/FP-Growth 算法

在数据挖掘中，寻找大型数据库中的频繁模式的任务非常重要，并在过去几年中被大规模研究。不幸的是，这项任务计算量很大，尤其是在存在大量模式的情况下。

FP-Growth 算法由 Han 在 中提出，是一种高效且可扩展的方法，它通过模式片段增长来挖掘完整的频繁模式集，并使用扩展的前缀树结构来存储关于频繁模式的压缩和关键信息，称为频繁模式树（FP-Tree）。在他的研究中，Han 证明了他的方法优于其他流行的挖掘频繁模式的方法，例如 Apriori 算法 和 TreeProjection 。在一些后续作品 中证明，FP-Growth 具有比其他方法更好的性能，包括 Eclat 和 Relim 。FP-Growth 算法的普及和效率促成了许多研究，这些研究提出了改进其性能的变体 。

本章介绍了该算法和一些变体，并讨论了 R 语言的特性以及在 R 中实现该算法以供使用的策略。接下来，提出了简要的结论和未来工作。

该算法

FP-Growth 算法是一种寻找频繁项集的替代方法，无需使用候选生成，从而提高性能。为此，它使用分治策略 。该方法的核心是使用一种称为频繁模式树（FP-Tree）的特殊数据结构，它保留了项集关联信息。

简单来说，该算法的工作原理如下：首先，它压缩输入数据库，创建 FP-Tree 实例来表示频繁项。完成第一步后，它将压缩后的数据库划分为一组条件数据库，每个数据库都与一个频繁模式相关联。最后，分别挖掘每个这样的数据库。使用这种策略，FP-Growth 减少了递归查找短模式的搜索成本，然后将它们连接成长频繁模式，提供了良好的选择性。

在大型数据库中，不可能将 FP-Tree 保存在主内存中。解决此问题的策略是首先将数据库划分为一组较小的数据库（称为投影数据库），然后从每个较小的数据库构建 FP-Tree。

接下来的几个小节将描述 FP-Tree 结构和 FP-Growth 算法，最后将提供一个示例，以便更轻松地理解这些概念。

FP-Tree 结构

频繁模式树（FP-Tree）是一种紧凑的结构，用于存储数据库中频繁模式的定量信息 。

Han 将 FP-Tree 定义为如下所示的树结构

1. 一个标记为“null”的根，其子节点是一组项前缀子树；
2. 项前缀子树中的每个节点都包含三个字段

1. 项名称：注册节点表示的项；
2. 计数：到达节点的路径部分所表示的事务数量；
3. 节点链接：链接到 FP-Tree 中下一个具有相同项名称的节点，如果不存在则为 null。

1. 频繁项表头表中的每个条目都包含两个字段

1. 项名称：与节点相同；
2. 节点链接头部：指向 FP-Tree 中第一个携带该项名称的节点的指针。

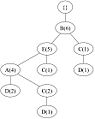
此外，频繁项表头表可以包含项的计数支持。下面的图 1 展示了一个 FP-Tree 的示例。

• 

图 1：来自 的 FP-Tree 示例。

Han 在 中定义的构建 FP-Tree 的原始算法如下所示，即算法 1。

算法 1：FP-Tree 构建

输入：事务数据库 DB 和最小支持阈值 ?。

输出：FP-Tree，DB 的频繁模式树。

方法：FP-Tree 按以下步骤构建。

1. 扫描事务数据库 DB 一次。收集 F，即频繁项集，以及每个频繁项的支持度。按支持度降序对 F 进行排序，得到 FList，即频繁项列表。
2. 创建 FP-Tree T 的根，并将其标记为“null”。对于 DB 中的每个事务 Trans，执行以下操作

• 选择 Trans 中的频繁项，并根据 FList 的顺序对它们进行排序。令 Trans 中排序后的频繁项列表为 [ p | P]，其中 p 是第一个元素，P 是其余列表。调用 insert tree([ p | P], T )。
• 函数 insert tree([ p | P], T ) 的执行方式如下。如果 T 存在子节点 N，使得 N.item-name = p.item-name，则将 N 的计数加 1；否则，创建一个新节点 N，其计数初始化为 1，其父链接指向 T，其节点链接通过节点链接结构指向具有相同项名称的节点。如果 P 不为空，则递归调用 insert tree(P, N )。

使用此算法，FP-Tree 在扫描数据库两次后构建完成。第一次扫描收集并排序频繁项集，第二次扫描构建 FP-Tree。

FP-Growth 算法

构建完 FP-Tree 后，就可以对其进行挖掘，以找到完整的频繁模式集。为了完成这项工作，Han 在 中提出了一组引理和性质，之后描述了 FP-Growth 算法，如下所示，即算法 2。

算法 2：FP-Growth

输入：一个数据库 DB，由根据算法 1 构建的 FP-Tree 表示，以及最小支持阈值 ?。

输出：完整的频繁模式集。

方法：调用 FP-growth(FP-tree, null)。

过程 FP-growth(Tree, a) {

(01) 如果 Tree 包含一条前缀路径，则 { // 挖掘单前缀路径 FP-Tree

(02) 令 P 为 Tree 的单前缀路径部分；

(03) 令 Q 为多路径部分，其中顶部分支节点被替换为 null 根；

(04) 对于路径 P 中节点的每个组合（记为 ß），执行以下操作

(05) 生成模式 ß ∪ a，其支持度 = ß 中节点的最小支持度；

(06) 令 freq pattern set(P) 为如此生成的模式集；

}

(07) 否则，令 Q 为 Tree；

(08) 对于 Q 中的每个项 ai，执行以下操作 { // 挖掘多路径 FP-Tree

(09) 生成模式 ß = ai ∪ a，其支持度 = ai .support；

(10) 构建 ß 的条件模式库，然后构建 ß 的条件 FP-Tree Tree ß；

(11) 如果 Tree ß ≠ Ø，则

(12) 调用 FP-growth(Tree ß , ß)；

(13) 令 freq pattern set(Q) 为如此生成的模式集；

}

(14) 返回 (freq pattern set(P) ∪ freq pattern set(Q) ∪ (freq pattern set(P) × freq pattern set(Q)))

}

当 FP 树包含单个前缀路径时，可以将完整的频繁模式集划分为三个部分生成：单个前缀路径 P、多路径 Q 以及它们的组合（第 01 到 03 行和第 14 行）。单个前缀路径的所得模式是其具有最小支持的子路径的枚举（第 04 到 06 行）。之后，定义多路径 Q（第 03 或 07 行）并处理由此产生的模式（第 08 到 13 行）。最后，在第 14 行，将组合的结果作为找到的频繁模式返回。

一个例子

本节提供一个简单的示例来说明先前算法的工作原理。原始示例可以在 中查看。

考虑以下交易，最小支持度为 3

	i(t)
1	FBAED
2	BCE
3	ABDE
4	ABCE
5	ABCDE
6	BCD

要构建 FP 树，首先计算频繁项的支持度并按降序排列，得到以下列表：{ B(6), E(5), A(4), C(4), D(4) }。然后，使用排序后的项目列表，如 图 2 所示，为每个交易迭代地构建 FP 树。

• 
  (a) 交易 1：BEAD
• 
  (b) 交易 2：BEC
• 
  (c) 交易 3：BEAD
• 
  (d) 交易 4：BEAC
• 
  (e) 交易 5：BEACD
• 
  (f) 交易 6：BCD

图 2：迭代构建 FP 树。

如图 3 所示，对 FP-Growth 的初始调用使用从算法 1 获得的 FP 树（如 图 2 (f) 所示），以在对投影树进行递归调用时处理之前提供的交易中的频繁模式。

使用深度优先策略，分别确定到项目 D、C、A、E 和 B 的投影树。首先递归处理 D 的投影树，投影 DA、DE 和 DB 的树。以类似的方式处理剩余的项目。在处理结束时，频繁项集为：{ DAE, DAEB, DAB, DEB, DA, DE, DB, CE, CEB, CB, AE, AEB, AB, EB }。

图 3：FP-Growth 算法递归调用发现的投影树和频繁模式。

FP-Growth 算法变体

如前所述，FP-Growth 算法的流行和效率促成了许多研究，这些研究提出了各种变体来提高其性能 。本节简要介绍其中一些。

DynFP-Growth 算法

DynFP-Growth ，重点关注基于两个观察到的问题的 FP-Tree 算法构建的改进

1. 对于相同的“逻辑”数据库，生成的 FP 树并不唯一；
2. 该过程需要对数据库进行两次完整扫描。

为了解决第一个问题，Gyorödi C. 等人 提出了使用支持降序排列以及词典排序的方法，从而确保了对于不同的“逻辑上等效”数据库，生成的 FP 树的唯一性。为了解决第二个问题，他们建议设计一种动态 FP 树重排序算法，并在检测到至少一项提升到更高阶时使用此算法。

此方法的一个重要特点是，当实际数据库更新时，无需重建 FP 树。只需再次执行算法，并考虑新交易和存储的 FP 树。

由于动态重排序过程，另一个提议的适应性是在原始结构中的修改，用双向链表替换单向链表以将树节点链接到标题，并在同一标题中添加一个主表。有关更多详细信息，请参阅 。

FP-Bonsai 算法

FP-Bonsai 通过使用 ExAnte 数据减少技术 减少（修剪）FP 树来提高 FP-Growth 性能。修剪后的 FP 树称为 FP-Bonsai。有关更多详细信息，请参阅 。

AFOPT 算法

Liu 在 中提出了 AFOPT 算法，该算法旨在从四个方面提高 FP-Growth 算法的性能

• 项目搜索顺序：当搜索空间被划分时，所有项目都按某种顺序排序。使用不同的项目搜索顺序，构造的条件数据库的数量可能会有很大差异；
• 条件数据库表示：条件数据库的遍历和构造成本在很大程度上取决于其表示；
• 条件数据库构建策略：物理地构建每个条件数据库可能很昂贵，会影响每个单独条件数据库的挖掘成本；
• 树遍历策略：使用自上而下的遍历策略，树的遍历成本最小。

有关更多详细信息，请参阅 。

NONORDFP 算法

Nonordfp 算法 的灵感来自 FP-Growth 算法的运行时间和空间需求。理论上的区别是主要数据结构（FP 树），它更紧凑，并且不需要在每个条件步骤中重建它。引入了使用 Trie 数据结构 的 FP 树的紧凑、内存高效表示，其内存布局允许更快的遍历、更快的分配以及可选的投影。有关更多详细信息，请参阅 。

FP-Growth* 算法

该算法由 Grahne 等人提出。^[16][19]，并基于他对使用 FP-Growth 计算频繁项集的 CPU 时间的结论。他们观察到 80% 的 CPU 时间用于遍历 FP-Tree。^[9] 因此，他们使用基于数组的数据结构结合 FP-Tree 数据结构来减少遍历时间，并结合了几种优化技术。有关详细信息，请参见^[16][19]。

PPV、PrePost 和 FIN 算法

这三种算法由 Deng 等人提出。^[20][21][22]，并基于三种新颖的数据结构，即节点列表^[20]、N-列表^[21] 和节点集^[22]，分别用于促进频繁项集的挖掘过程。它们基于 FP-Tree，每个节点都用前序遍历和后序遍历进行编码。与节点列表相比，N-列表和节点集更高效。这使得 PrePost ^[21] 和 FIN ^[22] 的效率高于 PPV ^[20]。有关详细信息，请参见^[20][21][22]。

R 中的数据可视化

通常，用于挖掘频繁项集的数据存储在文本文件中。可视化数据的第一步是将其加载到数据帧中（一个表示 R 中数据的对象）。

函数 read.table 可以以以下方式使用

var <- read.table(fileName, fileEncoding=value, header = value, sep = value)

Where:
  • var: the R variable to receive the loaded data.
  • fileName: is a string value with the name of the file to be loaded.
  • fileEncoding: to be used when the file has no-ASCII characters.
  • header: indicates that the file has headers (T or TRUE) or not (F or FALSE).
  • sep: defines the field separator character (“,”, “;” or “\t” for example)
  • Only the filename is a mandatory parameter.

R 中另一个用于加载数据的函数称为 scan。有关详细信息，请参见 R 数据导入/导出手册。

数据的可视化可以通过两种方式完成

• 使用变量名 (var) 以表格形式列出数据。
• 以及 summary(var) 以列出数据的摘要。

示例

> data <- read.table("boolean.data", sep=",", header=T)

> data
      A    B     C     D     E
1  TRUE TRUE FALSE  TRUE  TRUE
2 FALSE TRUE  TRUE FALSE  TRUE
3  TRUE TRUE FALSE  TRUE  TRUE
4  TRUE TRUE  TRUE FALSE  TRUE
5  TRUE TRUE  TRUE  TRUE  TRUE
6 FALSE TRUE  TRUE  TRUE FALSE

> summary(data)
     A              B               C               D               E
 Mode :logical   Mode:logical   Mode :logical   Mode :logical   Mode :logical
 FALSE:2         TRUE:6         FALSE:2         FALSE:2         FALSE:1
 TRUE :4         NA's:0         TRUE :4         TRUE :4         TRUE :5
 NA's :0                        NA's :0         NA's :0         NA's :0

在上面的示例中，使用简单的二进制数据库“boolean.data”中的数据加载到数据帧变量 data 中。在命令行中键入变量名，将打印其内容，键入 summary 命令将打印每个项目的频率出现情况。summary 函数的工作方式不同。它取决于变量中数据的类型，有关详细信息，请参见^[23][24][25]。

之前介绍的函数可能很有用，但对于频繁项集数据集，使用一个名为 arules ^[26] 的特定包可以更好地可视化数据。

使用 arules，提供了一些函数

• read.transactions：用于将数据库文件加载到变量中。
• inspect：用于列出事务。
• length：返回事务数量。
• image：绘制包含所有事务的矩阵格式的图像。
• itemFrequencyPlot：计算每个项目的频率并将其绘制在条形图中。

示例

> data <- read.transactions("basket.data", format="basket", sep = ",")

> data
transactions in sparse format with
 6 transactions (rows) and
 5 items (columns)

> inspect(data)
  items
1 {A,
   B,
   D,
   E}
2 {B,
   C,
   E}
3 {A,
   B,
   D,
   E}
4 {A,
   B,
   C,
   E}
5 {A,
   B,
   C,
   D,
   E}
6 {B,
   C,
   D}

> length(data)
[1] 6

> image(data)

> itemFrequencyPlot(data, support=0.1)

在这个例子中，我们可以看到在命令行中使用变量名的区别。从事务中，只打印了行数（事务）和列数（项目）。image(data) 和 itemFrequencyPlot(data, support = 0.1) 的结果分别在下面的图 4 和图 5 中给出。

• 

图 4：image(data) 调用的结果。

• 

图 5：itemFrequencyPlot(data, support = 0.1) 调用的结果。

R 中的实现

R ^{[23][24][25][27][28]} 提供了用于数据操作、计算和图形显示的几种工具，非常适用于数据分析和挖掘。它既可以用作统计库，也可以用作编程语言。

作为统计库，它提供了一组用于汇总数据、矩阵工具、概率分布、统计模型和图形过程的函数。

作为编程语言，它提供了一组函数、命令和方法来实例化和管理不同类型对象的的值（包括列表、向量和矩阵）、用户交互（从控制台输入和输出）、控制语句（条件语句和循环语句）、函数的创建、对外部资源的调用以及创建包。

本章并没有完成对 R 资源的详细介绍，而是重点关注使用 R 实现算法或在 R 中使用的挑战。但是，为了更好地理解 R 的功能，在附录 A 中提供了一些基于^[28] 的基本示例。

使用 R 实现算法通常需要创建复杂的对象来表示要处理的数据结构。此外，可能需要实现复杂函数来处理这些数据结构。考虑到使用 R 实现 FP-Growth 算法的具体情况，仅使用 R 资源可能很难表示和处理 FPTree。此外，出于性能原因，使用其他语言实现算法并将其与 R 集成可能很有趣。使用其他语言的其他原因是获得更好的内存管理以及使用现有的包^[29]。

有两种方法可以将 R 与其他语言集成，下面将简要介绍：创建包和使用接口函数进行外部调用。^[24] 接下来介绍了在这项工作中使用的 FP-Growth 实现以及将其与 R 集成的努力。对于两者，都需要安装 RTools。

创建包

包是将用其他语言实现的可选代码加载到 R 中的一种机制。^[24] R 发行版本身包含大约 25 个包，本 WikiBook 中使用的一些额外包可以列出

• aRules
• arulesNBMiner
• arulesSequences
• cluster

要创建包，需要遵循一些规范。R 包的来源包含在下面描述的目录结构中

• 根目录：包含 DESCRIPTION 文件和一些可选文件（INDEX、NAMESPACE、configure、cleanup、LICENCE、COPYING 和 NEWS）的根目录。
• R：仅包含 R 代码文件，这些文件可以通过 R 命令 source(filename) 执行以创建用户使用的 R 对象。或者，此目录可以包含一个文件 sysdata.rda。此文件包含在 R 控制台执行中创建的 R 对象的保存图像。
• data：旨在包含数据文件，这些文件可以通过延迟加载提供或使用函数 data() 加载。这些数据文件可以来自三种不同类型：纯 R 代码（.r 或 .R）、表格（.tab、.txt 或 .csv）或来自 R 控制台的保存数据（.RData 或 .rda）。一些额外的压缩文件可用于表格文件。
• demo：包含纯 R 代码中的脚本（用于使用函数 demo() 运行），这些脚本演示了包中的一些功能。
• exec：可能包含包需要的其他可执行文件，通常是用于 shell、Perl 或 Tcl 等解释器的脚本。
• inst：其内容将在构建后复制到安装目录，其 Makefile 可以创建要安装的文件。可能包含所有旨在供最终用户查看的信息文件。
• man：应仅包含包中对象的文档文件（使用特定的 R 文档格式）。空 man 目录会导致安装错误。
• po：用于与国际化相关的文件，换句话说，用于翻译错误和警告消息。
• src：包含源代码、头文件、makevars 和 makefile。支持的语言有：C、C++、FORTRAN 77、Fortran 9x、Objective C 和 Objective C++。在一个包中混合所有这些语言是不可能的，但混合 C 和 FORTRAN 77 或 C 和 C++ 似乎很成功。但是，有一些方法可以从其他包中进行使用。
• tests：用于其他特定于包的测试代码。

创建源代码包后，必须在操作系统控制台的命令行中安装它。

R CMD INSTALL <parameters>

或者，可以使用 R 控制台中的命令行从 R 中下载并安装包。

> install.packages(<parameters>)

请参阅 安装和管理手册 ，了解详细信息。

安装后，需要使用 R 控制台中的命令行加载包才能使用它。

> library(packageName)

使用接口函数进行外部调用

使用接口函数进行外部调用是一种简单的方法，可以无需遵守之前描述的所有规则来创建 R 包，即可使用外部实现。

首先，代码需要包含 R.h 头文件，该文件随 R 安装一起提供。

要编译源代码，需要在操作系统命令行中使用 R 编译器。

> R CMD SHLIB <parameters>

要用于 R 的编译代码需要在类 Unix 操作系统中作为共享对象加载，或在 Windows 操作系统中作为 DLL 加载。要加载或卸载它，可以使用 R 控制台中的命令。

> dyn.load(fileName)
> dyn.unload(fileName)

加载后，可以使用以下函数之一调用外部代码。

• .C
• .Call
• .Fortran
• .External

下面展示了两个简单的示例，使用 .C 函数。

示例 1：Hello World

## C code in file example1.c

#include <R.h>

Void do_stuff ()
{
   printf("\nHello, I'm in a C code!\n");
}


## R code in file example.R

dyn.load("example1.dll")

doStuff <-
function (){
    tmp <- .C("do_stuff")
	rm(tmp)
	return(0)
}

doStuff()


## Compiling code in OS command line

C:\R\examples>R CMD SHLIB example1.c
gcc -I"C:/PROGRA~1/R/R-212~1.0/include" -O3 -Wall -std=gnu99 -c example1.c -o example1.o
gcc -shared -s -static-libgcc -o example1.dll tmp.def example1.o -LC:/PROGRA~1/R/R-212~1.0/bin/i386 -lR


## Output in R console

> source("example1.R")

Hello, I'm in a C code!
>

示例 2：使用整数向量调用 C

##C code in file example2.c

#include <R.h>

void doStuff(int *i) {
    i[0] = 11;
}


## Output in R console

> dyn.load("example2.dll")
> a <- 1:10
> a
 [1]  1  2  3  4  5  6  7  8  9 10
> out <- .C("doStuff", b = as.integer(a))
> a
 [1]  1  2  3  4  5  6  7  8  9 10
> out$b
 [1] 11  2  3  4  5  6  7  8  9 10

FP-Growth 实现

此工作中使用的 FP-Growth 实现由 Christian Borgelt 实现，他是欧洲软计算中心的首席研究员。他还实现了 arules 包 中用于 Eclat 和 Apriori 算法的代码。源代码可以从他的个人网站下载。

正如 Borgelt 所描述的那样，核心操作的实现变体（计算 FP 树的投影）有两种。此外，投影的 FP 树可以选择通过删除变得不再频繁的项来进行修剪（使用 FP-Bonsai 方法）。

源代码分为三个主要文件夹（包）。

• fpgrowth：包含实现算法并管理 FP 树的主要文件；
• tract：管理项集、事务及其报告；
• util：用于 fpgrowth 和 tract 的工具。

从操作系统命令行调用此实现的语法为

> fpgrowth [options] infile [outfile [selfile]]
-t#      target type                              (default: s)
         (s: frequent, c: closed, m: maximal item sets,
          g: generators, r: association rules)
-m#      minimum number of items per set/rule     (default: 1)
-n#      maximum number of items per set/rule     (default: no limit)
-s#      minimum support of an item set/rule      (default: 10%)
-S#      maximum support of an item set/rule      (default: 100%)
         (positive: percentage, negative: absolute number)
-o       use original rule support definition     (body & head)
-c#      minimum confidence of an assoc. rule     (default: 80%)
-e#      additional evaluation measure            (default: none)
-a#      aggregation mode for evaluation measure  (default: none)
-d#      threshold for add. evaluation measure    (default: 10%)
-i       invalidate eval. below expected support  (default: evaluate all)
-p#      (min. size for) pruning with evaluation  (default: no pruning)
         (< 0: weak forward, > 0 strong forward, = 0: backward pruning)
-q#      sort items w.r.t. their frequency        (default: 2)
         (1: ascending, -1: descending, 0: do not sort,
          2: ascending, -2: descending w.r.t. transaction size sum)
-A#      variant of the fpgrowth algorithm to use (default: c)
-x       do not prune with perfect extensions     (default: prune)
-l#      number of items for k-items machine      (default: 16)
         (only for variants s and d, options -As or -Ad)
-j       do not sort items w.r.t. cond. support   (default: sort)
         (only for algorithm variant c, option -Ac)
-u       do not use head union tail (hut) pruning (default: use hut)
         (only for maximal item sets, option -tm)
-F#:#..  support border for filtering item sets   (default: none)
         (list of minimum support values, one per item set size,
         starting at the minimum size, as given with option -m#)
-R#      read item selection/appearance indicators
-P#      write a pattern spectrum to a file
-Z       print item set statistics (number of item sets per size)
-N       do not pre-format some integer numbers   (default: do)
-g       write item names in scanable form (quote certain characters)
-h#      record header  for output                (default: "")
-k#      item separator for output                (default: " ")
-I#      implication sign for association rules   (default: " <- ")
-v#      output format for set/rule information   (default: " (%S)")
-w       integer transaction weight in last field (default: only items)
-r#      record/transaction separators            (default: "\n")
-f#      field /item        separators            (default: " \t,")
-b#      blank   characters                       (default: " \t\r")
-C#      comment characters                       (default: "#")
-!       print additional option information
infile   file to read transactions from           [required]
outfile  file to write item sets/assoc. rules to  [optional]

可以选择每个集合的项数限制、最小支持度、评估度量、配置输入和输出格式等等。

使用 test1.tab 示例文件（随源代码提供）作为输入文件、test1.out 和最小支持度为 30% 对 FP-Growth 进行简单调用，其结果如下所示。

C:\R\exec\fpgrowth\src>fpgrowth -s30 test1.tab test1.out
fpgrowth - find frequent item sets with the fpgrowth algorithm
version 4.10 (2010.10.27)        (c) 2004-2010   Christian Borgelt
reading test1.tab ... [5 item(s), 10 transaction(s)] done [0.00s].
filtering, sorting and recoding items ... [5 item(s)] done [0.00s].
reducing transactions ... [8/10 transaction(s)] done [0.00s].
writing test1.out ... [15 set(s)] done [0.00s].

结果显示了一些关于版权的信息和一些执行数据，例如项数、事务数和频繁集数（本例中为 21 个）。输入和输出文件的内容如下所示。

输入文件内容

a b c
a d e
b c d
a b c d
b c
a b d
d e
a b c d
c d e
a b c

输出文件内容

e d  (30.0)
e  (30.0)
a c b  (40.0)
a c  (40.0)
a d b  (30.0)
a d  (40.0)
a b  (50.0)
a  (60.0)
d b c  (30.0)
d b  (40.0)
d c  (40.0)
d  (70.0)
c b  (60.0)
c  (70.0)
b  (70.0)

从 R 调用 FP-Growth

如前所述，要创建一个包，需要遵守几个规则，创建标准目录结构和内容，以使外部源代码可用。前面介绍了另一种方法，即创建共享对象或 DLL，并使用特定的 R 函数（.C、.CALL 等等）调用它。

从头开始做将现有代码改编成一个包的工作可能是一项艰巨的任务，需要花费大量时间。一个有趣的方法是迭代地创建和改编共享对象或 DLL，并进行测试以验证它，并在一些迭代后改进改编，当获得满意的结果后，开始进行包版本的工作。

使 C 实现可用于 R 的迭代意图如下所示。

1. 创建一个简单的命令行调用，不带参数，只对原始源代码（fpgrowth.c 文件）进行两个更改。

• 将主函数重命名为 FP-Growth，并使用相同的签名；
• 创建一个要从 R 中调用的函数，从配置文件创建参数（仅包含一个与命令行语法相同的字符串，将其分解成一个数组，以用作 FP-Growth 函数的参数数组）；

2. 使用 R 编译命令编译代码项目，包括 R.h 读取器文件，并使用 R 调用它；

3. 实施来自 R 调用的输入参数，消除配置文件的使用，包括更改以定义输入文件名以用于 R 中的数据帧；

4. 将输出准备成一个 R 数据帧，以返回到 R；

5. 创建 R 包。

第一次迭代可以轻松完成，没有任何意外。

不幸的是，第二次迭代看起来也很容易完成，但在实践中却证明非常困难。R 编译命令不能与 makefile 一起使用，因此无法使用它来编译原始代码。经过一些实验后，策略改为使用改编后的代码构建一个库，没有创建要从 R 中调用的函数，然后创建一个包含此函数并使用编译后的库的新代码。接下来，从 R 调用新编译的 DLL 会引发执行错误。在调试执行过程中，浪费了大量时间，发现创建库的一些编译配置是错误的。为了解决这个问题，进行了一些测试，创建了一个可执行版本，使用操作系统命令行运行它，直到所有执行错误都得到解决。然而，解决了这些错误后，又发现了另一个意外的行为。从 R 控制台调用使用 R 命令编译的版本，在加载 DLL 函数时，出现了 cygwin 版本不兼容的错误。尝试了很多实验，更改编译参数、cygwin 的不同版本等等，但都没有成功（这些测试只在 Windows 操作系统下进行）。因此，在第二次迭代中没有取得成功，后面的步骤就变得很困难。

第三和第四次迭代中预期的主要挑战是将 R 数据类型和结构与其在 C 语言中的对应物进行接口，无论是用于数据集输入和要转换为内部使用的其他输入参数，还是用于创建要返回到 R 的输出数据集。另一种方法是改编所有代码以使用接收到的数据。但是，这似乎更复杂。

第五次迭代看起来像是一项官僚工作。一旦代码完全改编并验证，创建额外的目录和所需内容应该是一件容易的事。

结论和未来工作

本章介绍了一种用于挖掘数据库中频繁模式的有效且可扩展的算法：FP-Growth。该算法使用了一种有用的数据结构 FP 树来存储关于频繁模式的信息。还介绍了该算法的实现。此外，还介绍了 R 语言的一些特性以及将算法源代码改编以在 R 中使用的实验。我们可以观察到，进行这种改编是一项艰巨的任务，无法在短时间内完成。不幸的是，还没有时间来完成这种改编。

作为一项未来工作，将对更好地理解 R 中外部资源的实现以及完成本工作中提出的任务，并在随后将结果与 R 中可用的其他频繁项集挖掘算法进行比较，会很有趣。

附录 A：R 语句示例

一些基于 的基本示例。

获取有关函数的帮助

> help(summary)
> ?summary

创建对象

> perceptual <- 1.2

数字表达式

> z <- 5
> w <- z^2
> y <- (34 + 90) / 12.5

打印对象值

> w
[1] 25

创建向量

> v <- c(4, 7, 23.5, 76.2, 80)

向量运算

> x <- sqrt(v)
> v1<- c(4, 6, 87)
> v2 <- c(34, 32.4, 12)
> v1 + v2
[1] 38.0 38.4 99.0

分类数据

> s <- c("f", "m", "m", "f")
> s
[1] "f" "m" "m" "f"
> s <- factor(s)
> s
[1] f m m f
Levels: f m
> table(s)
s
f m
2 2

序列

> x <- 1:1000
> y <- 5:0
> z <- seq(-4, 1, 0.5) # create a sequence starting in -4, stopping in 1 
                       # with an increment of 0.5
> w <- rnorm(10) # create a random sequence of 10 numeric values
> w <- rnorm(10, mean = 10, sd = 3) # create a normal distribution of 
                                    # 10 numeric values with mean of 10
                                    # and standard deviation of 3

矩阵

> m1 <- matrix(c(45,  23,  66,  77,  33,  44),  2,  3)
> m1
        [,1]   [,2]   [,3]
[1,]     45     66     33
[2,]     23     77     44
> m2 <- matrix(c(12,  65,  32,  7,  4,  78),  2,  3)
> m2
        [,1]   [,2]   [,3]
[1,]     12     32      4
[2,]     65      7     78
> m1 + m2
        [,1]   [,2]   [,3]
[1,]     57     98     37
[2,]     88     84    122

列表

> student <- list(nro = 34453, name = "Marie", scores = c(9.8, 5.7, 8.3))
> student[[1]]
[1] 34353
> student$nro
[1] 34353

数据框（表示数据库表格）

> scores.inform <- data.frame(nro = c(2355, 3456, 2334, 5456),
+ team = c("tp1", "tp1", "tp2", "tp3"), 
+ score = c(10.3, 9.3, 14.2, 15))
> scores.inform
    nro    team   score
1  2355     tp1    10.3
2  3456     tp1     9.3
3  2334     tp2    14.2
4  5456     tp3    15.0
> scores.inform[score > 14,]
    nro    team   score
3  2334     tp2    14.2
4  5456     tp3    15.0
> team
[1]  tp1  tp1  tp2  tp3
Levels:  tp1  tp2  tp3

条件语句

> if (x > 0) y <- z / x else y <- z
> if (x > 0) {
+    cat('x is positive.\n')
+    y <- z / x
+} else {
+    cat('x isn't positive!\n')
+    y <- z
+}

case 语句

> sem <- "green"
> switch(sem, green = "continue", yellow = "attention", red = "stop")
[1] "continue"

循环语句

> x <- rnorm(1)
> while (x < -0.3) {
+    cat("x=", x, "\t")
+    x <- rnorm(1)
+  }

> text  <-  c()
> repeat  {
+   cat('Type a phrase?  (empty to quit) ')
+   fr  <-  readLines(n=1)
+   if  (fr  ==  '')  break  else  texto  <-  c(texto,fr)
+}

> x <- rnorm(10)
> k <- 0
> for(v in x)  {
+   if(v > 0)
+     y <- v
+   else y <- 0
+     k <- k + y
+  }

创建和调用函数

> cel2far <- function(cel) {
+   res  <-  9/5  *  cel  +  32
+   res
+ }
> cel2far(27.4)
[1]  81.32
> cel2far(c(0,  -34.2,  35.6,  43.2))
[1]  32.00  -29.56    96.08  109.76