密度泛函理论/Hartree–Fock 方法

Hartree-Fock (HF) 或自洽场 (SCF)

在 计算物理学 和 化学 中，Hartree–Fock (HF) 方法是一种近似方法，用于确定 波函数 和 量子多体系统 在 稳态 中的能量。

Hartree–Fock 方法通常假设系统的精确的，N 体波函数可以用单个 Slater 行列式（当粒子是 费米子 时）或单个 永久行列式（当粒子是 玻色子 时）来近似，这两个行列式分别由 N 个 自旋轨道 组成。 通过调用 w:变分法，可以推导出 N 个自旋轨道的 N 个耦合方程组。 这些方程组的解将给出系统的 Hartree–Fock 波函数和能量。

特别是在较早的文献中，Hartree–Fock 方法也被称为自洽场方法 (SCF)。 在推导出现在被称为 Hartree 方程 的 薛定谔方程 的近似解时，哈特里 要求从电荷分布计算出的最终场与假设的初始场“自洽”。 因此，自洽是解的一个要求。 非线性 Hartree–Fock 方程的解表现得好像每个粒子都受到所有其他粒子产生的平均场的约束（参见下面 Fock 算符），因此术语得以延续。 这些方程几乎普遍通过 迭代法 求解，尽管 不动点迭代 算法并不总是收敛。^[1] 这种求解方案并非唯一可能的方案，也并非 Hartree–Fock 方法的本质特征。

Hartree–Fock 方法通常应用于求解原子、分子、纳米结构^[2] 和固体的 薛定谔方程，但它也广泛应用于 核物理学 中。 （参见 Hartree–Fock–Bogoliubov 方法，了解其在 核结构 理论中的应用）。 在 原子结构 理论中，计算可能是针对具有许多激发能级的谱线，因此 Hartree–Fock 原子方法 假设波函数是具有明确 量子数 的单个 组态态函数，并且能级并不一定是 基态。

对于原子和分子，Hartree–Fock 解是大多数更准确地描述多电子系统的方案的中心起点。

本文的其余部分将重点介绍适用于具有原子作为特例的分子 的电子结构理论中的应用。 这里的讨论仅针对限制性 Hartree–Fock 方法，其中原子或分子是闭壳层系统，所有轨道（原子或分子）都是双占据的。 开壳 系统，其中一些电子没有配对，可以通过两种 Hartree–Fock 方法之一处理

• w:限制性开壳 Hartree–Fock (ROHF)
• w:无限制 Hartree–Fock (UHF)

历史

Hartree–Fock 方法的起源可以追溯到 20 世纪 20 年代末，当时距 1926 年发现 w:薛定谔方程 只有几年时间。 1927 年，D. R. 哈特里 提出了一种程序，他称之为自洽场方法，用于计算原子和离子的近似波函数和能量。 哈特里的灵感来自于 20 世纪 20 年代初的一些早期的半经验方法（由 E. Fues、R. B. 林赛 和他自己提出），这些方法被设定在玻尔的 w:旧量子论 框架中。

在w:玻尔模型中，具有w:主量子数 n 的状态的能量以原子单位表示为 $E=-1/n^{2}$。从原子光谱中观察到，多电子原子的能级可以通过应用玻尔公式的修正版本来很好地描述。通过引入w:量子亏损 *d* 作为经验参数，通用原子的能级可以用公式$E=-1/(n+d)^{2}$很好地近似，从这个意义上说，可以相当好地重现观察到的w:X射线区域的跃迁能级（例如，参见w:莫塞莱定律中的经验讨论和推导）。非零量子亏损的存在归因于电子-电子排斥，这种排斥在孤立的氢原子中显然不存在。这种排斥导致了裸核电荷的局部屏蔽。这些早期的研究人员后来引入了包含其他经验参数的其他势，希望更好地重现实验数据。

哈特里试图消除经验参数，并从基本的物理原理，即从头算，来求解多体时间无关薛定谔方程。他提出的第一个求解方法被称为哈特里方法。然而，哈特里的许多同时代人并不理解哈特里方法背后的物理推理：它在许多人看来包含经验元素，其与多体薛定谔方程解的联系也不清楚。然而，在 1928 年，J. C. 斯莱特 和 J. A. 冈特独立地证明，哈特里方法可以通过将w:变分原理应用于w:试探波函数（作为单粒子函数的乘积）来建立在更合理的理论基础上。

1930 年，斯莱特和V. A. 福克 独立地指出，哈特里方法不尊重波函数的反对称性原理。哈特里方法使用w:泡利不相容原理的旧形式，禁止两个电子处于相同量子态。然而，这在其忽略w:量子统计方面被证明是根本不完整的。

随后证明，w:斯莱特行列式，即海森堡和狄拉克在 1926 年首次使用的单粒子轨道w:行列式，微不足道地满足了精确解的反对称性质，因此它是将w:变分原理应用于w:试探波函数的合适选择。然后，可以将原始的哈特里方法看作是通过忽略交换来对哈特里-福克方法进行的近似。福克最初的方法过分依赖w:群论，对于当代物理学家来说过于抽象，难以理解和实施。1935 年，哈特里重新制定了该方法，使其更适合计算目的。

尽管哈特里-福克方法的物理图像更加准确，但在 20 世纪 50 年代电子计算机出现之前，由于其计算量远大于早期的哈特里方法和经验模型，因此很少使用。最初，哈特里方法和哈特里-福克方法都专门应用于原子，其中系统的球对称性允许人们极大地简化问题。这些近似方法经常（并且仍然）与w:中心场近似一起使用，以强制要求同一壳层中的电子具有相同的径向部分，并将变分解限制为自旋本征函数。即使如此，手工求解中等大小原子的哈特里-福克方程也是一项艰巨的任务；小型分子需要的计算资源远远超过 1950 年之前所能提供的资源。

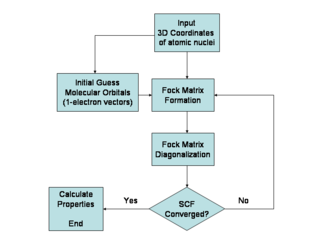
哈特里-福克算法

哈特里-福克方法通常用于求解w:玻恩-奥本海默近似中描述的多电子原子或分子的时间无关薛定谔方程。由于没有已知的用于多电子系统的解（氢原子和双原子氢阳离子是著名的单电子例外），因此该问题是通过数值方法解决的。由于哈特里-福克近似引入的非线性，这些方程使用非线性方法（例如w:迭代）来求解，这也导致了“自洽场方法”的名称。

近似

哈特里-福克方法为了处理这一任务，做出了五个主要简化。

• w:玻恩-奥本海默近似本身就被假设成立。完整的分子波函数实际上是每个原子核的坐标以及电子的坐标的函数。
• 通常，相对论效应被完全忽略。动量算符被假定为完全非相对论性的。
• 变分解被假定为有限数量基函数的w:线性组合，这些基函数通常（但并非总是）被选为w:正交的。有限基组被假定为近似完全的。
• 每个w:能量本征函数被假定可以用单个w:斯莱特行列式来描述，即单电子波函数（即轨道）的反对称乘积。
• 平均场近似隐含其中。由于偏离该假设而产生的影响被称为w:电子关联，对于自旋相反的电子来说，这些影响被完全忽略，但对于自旋平行的电子来说，这些影响被考虑在内。 （电子关联不应与电子交换混淆，电子交换在哈特里-福克方法中得到了充分考虑）。

对最后两个近似的放松导致了许多所谓的w:后哈特里-福克方法。

简化后的算法流程图，展示了哈特里-福克方法

轨道的变分优化

变分原理指出，对于一个时间无关的哈密顿算符，任何试探波函数的能量期望值都大于或等于对应于给定哈密顿算符的真实基态波函数。因此，Hartree-Fock 能量是给定分子真实基态能量的上限。在 Hartree-Fock 方法的背景下，最佳的可能解是在 *Hartree-Fock 极限* 处；也就是说，随着基组接近完备性，Hartree-Fock 能量的极限。（另一个是 *完全 CI 极限*，其中 Hartree-Fock 理论如上所述的最后两个近似完全被取消。只有当这两个极限都达到时，才能获得精确解，直至 Born-Oppenheimer 近似。）Hartree-Fock 能量是单个 Slater 行列式的最小能量。

Hartree-Fock 方法的起点是一组近似的单电子波函数，称为 *自旋轨道*。对于原子轨道计算，这些通常是氢原子（只有一个电子但具有适当核电荷的原子）的轨道。对于分子轨道或晶体计算，初始的近似单电子波函数通常是原子轨道线性组合 (LCAO)。

上面的轨道只以平均方式解释了其他电子的存在。在 Hartree-Fock 方法中，其他电子的影响是在平均场理论的背景下考虑的。通过要求轨道最小化相应 Slater 行列式的能量来优化轨道。轨道上的结果变分条件导致了一个新的单电子算符，即 Fock 算符。在最小值处，占据轨道是 Fock 算符的特征解，通过它们自身之间的酉变换。Fock 算符是一个有效的单电子哈密顿算符，是两个项的总和。第一个是每个电子的动能算符之和、核间排斥能以及核-电子库仑吸引项之和。第二个是电子之间的库仑排斥项，在平均场理论描述中；系统中每个电子的净排斥能，它是通过将分子中的所有其他电子视为负电荷的平滑分布来计算的。这是 Hartree-Fock 方法固有的主要简化，等效于上面列表中的第五个简化。

由于 Fock 算符取决于用于构建相应 Fock 矩阵的轨道，因此 Fock 算符的特征函数反过来是新的轨道，可用于构建新的 Fock 算符。通过这种方式，Hartree-Fock 轨道以迭代方式优化，直到总电子能量的变化低于预定义的阈值。通过这种方式，计算出一组自洽的单电子轨道。然后，Hartree-Fock 电子波函数是由这些轨道构成的 Slater 行列式。根据量子力学的基本假设，Hartree-Fock 波函数可用于在 Hartree-Fock 方法和所采用的近似的框架内计算任何所需的化学或物理性质。

数学公式

Slater 行列式

在量子力学中，**Slater 行列式**是一个表达式，描述了满足反对称要求的多费米子系统的波函数，因此通过交换费米子改变符号而满足泡利不相容原理。 它的名字来源于它的发现者，John C. Slater，他发表了 Slater 行列式作为一种通过使用矩阵来确保波函数反对称性的方法。 Slater 行列式源于对电子集合的波函数的考虑，每个电子都有一个称为自旋轨道的波函数，$\chi (\mathbf {x} )$，其中 $\mathbf {x}$ 表示单个电子的位置和自旋。同一自旋轨道内的两个电子不会产生任何波函数。

决议

双粒子情况

近似多粒子系统波函数的最简单方法是取单个粒子适当选择的正交波函数的乘积。对于具有空间坐标 $\mathbf {x} _{1}$ 和 $\mathbf {x} _{2}$ 的双粒子情况，我们有

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2})=\chi _{1}(\mathbf {x} _{1})\chi _{2}(\mathbf {x} _{2}).$

此表达式在 Hartree–Fock 方法 中用作 Ansatz 来表示多粒子波函数，被称为 Hartree 积。然而，它并不适用于 费米子，因为上述波函数不是反对称的，而它必须是 费米子 符合 泡利不相容原理 的要求。反对称波函数可以用以下数学方式描述：

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2})=-\Psi (\mathbf {x} _{2},\mathbf {x} _{1})$

此关系对于 Hartree 积并不成立。因此，Hartree 积不满足泡利不相容原理。这个问题可以通过取两个 Hartree 积的 线性组合 来克服

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2})={\frac {1}{\sqrt {2}}}\{\chi _{1}(\mathbf {x} _{1})\chi _{2}(\mathbf {x} _{2})-\chi _{1}(\mathbf {x} _{2})\chi _{2}(\mathbf {x} _{1})\}$

$={\frac {1}{\sqrt {2}}}{\begin{vmatrix}\chi _{1}(\mathbf {x} _{1})&\chi _{2}(\mathbf {x} _{1})\\\chi _{1}(\mathbf {x} _{2})&\chi _{2}(\mathbf {x} _{2})\end{vmatrix}}$

其中系数是 归一化因子。此波函数现在是反对称的，不再区分费米子，也就是说：无法为特定粒子指定序数，给定的索引是可互换的。此外，如果两个费米子的任何两个波函数相同，它也变为零。这等同于满足泡利不相容原理。

泛化

此表达式可以推广到任意数量的费米子，方法是将其写成 行列式。对于一个具有 *N* 个电子的系统，斯莱特行列式定义为

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{N})={\frac {1}{\sqrt {N!}}}\left|{\begin{matrix}\chi _{1}(\mathbf {x} _{1})&\chi _{2}(\mathbf {x} _{1})&\cdots &\chi _{N}(\mathbf {x} _{1})\\\chi _{1}(\mathbf {x} _{2})&\chi _{2}(\mathbf {x} _{2})&\cdots &\chi _{N}(\mathbf {x} _{2})\\\vdots &\vdots &\ddots &\vdots \\\chi _{1}(\mathbf {x} _{N})&\chi _{2}(\mathbf {x} _{N})&\cdots &\chi _{N}(\mathbf {x} _{N})\end{matrix}}\right|\equiv \left|{\begin{matrix}\chi _{1}&\chi _{2}&\cdots &\chi _{N}\\\end{matrix}}\right|,$

其中在最终表达式中，引入了紧凑的符号：费米子坐标的归一化常数和标签是理解的 - 只有波函数被展示。对于双粒子情况，哈特里积的线性组合可以清楚地看出与N = 2 的斯莱特行列式相同。可以看出，使用斯莱特行列式确保了从一开始就得到一个反对称函数；对称函数被自动拒绝。同样，使用斯莱特行列式确保了符合 泡利不相容原理。事实上，如果集合 {χ_i } 是 线性相关的，则斯莱特行列式消失。特别地，当两个（或更多）自旋轨道相同时，情况就是这样。在化学中，人们用这样的说法来表达这一事实：没有两个电子可以占据同一个自旋轨道。一般情况下，斯莱特行列式是通过 拉普拉斯展开来计算的。在数学上，斯莱特行列式是一个反对称张量，也被称为 外积。

在 哈特里-福克理论中，单个斯莱特行列式被用作电子波函数的近似值。在更精确的理论中（例如 组态相互作用 和 多组态自洽场），需要斯莱特行列式的线性组合。

S. F. Boys 提出了“detor”这个词来描述一般类型的斯莱特行列式， 但这个词很少使用。

与受泡利不相容原理约束的 费米子 不同，两个或多个 玻色子 可以占据相同的单粒子量子态。描述相同 玻色子 系统的波函数在粒子交换下是对称的，可以用 永久行列式 来展开。

福克算符

主条目：w:福克矩阵

因为 w:电子分子哈密顿量 的电子-电子排斥项涉及两个不同电子的坐标，所以有必要以近似的方式重新表达它。在这种近似下（在 哈特里-福克算法 中概述），除核-核排斥项之外的所有精确哈密顿量的项都被重新表达为下面概述的单电子算子的总和，用于闭壳层原子或分子（每个空间轨道中有两个电子）。 每个算符符号后面的“(1)”只是表示算符本质上是1电子的。

${\hat {F}}[\{\phi _{j}\}](1)={\hat {H}}^{\text{core}}(1)+\sum _{j=1}^{N/2}[2{\hat {J}}_{j}(1)-{\hat {K}}_{j}(1)]$

其中

${\hat {F}}[\{\phi _{j}\}](1)$

是由轨道 $\phi _{j}$ 生成的单电子福克算符，并且

${\hat {H}}^{\text{core}}(1)=-{\frac {1}{2}}\nabla _{1}^{2}-\sum _{\alpha }{\frac {Z_{\alpha }}{r_{1\alpha }}}$

是单电子核心 哈密顿算符。 同时

${\hat {J}}_{j}(1)$

是 库仑算符，定义了第 j 个轨道中两个电子之间相互排斥的能量。 最后

${\hat {K}}_{j}(1)$

是 交换算符，定义了由于总 n 电子波函数的反称性而产生的电子交换能量。 这个（所谓的）“交换能量”算符 K 只是斯莱特行列式的一个产物。 寻找哈特里-福克单电子波函数现在等效于求解本征函数方程

${\hat {F}}(1)\phi _{i}(1)=\epsilon _{i}\phi _{i}(1)$

其中 $\phi _{i}\;(1)$ 是一组单电子波函数，称为哈特里-福克分子轨道。

原子轨道线性组合

主要文章: w:基组 (化学) 和 w:基组

通常，在现代的哈特里-福克计算中，单电子波函数用 原子轨道的线性组合 近似。 这些原子轨道被称为 斯莱特型轨道。 此外，为了节省大量的计算时间，使用的“原子轨道”实际上是由一个或多个 高斯型轨道 的线性组合组成的，而不是斯莱特型轨道。

在实践中，使用了各种基组，其中大多数由高斯函数组成。在某些应用中，为了产生一组正交基函数，会执行正交化方法，例如w:Gram-Schmidt过程。原则上，当计算机通过将w:重叠矩阵有效地转换为w:单位矩阵来求解Roothaan-Hall方程时，这可以节省计算时间。然而，在大多数用于分子Hartree-Fock计算的现代计算机程序中，由于正交化的数值成本高，以及用于求解w:广义特征值问题（Roothaan-Hall方程就是一个例子）的更有效、通常是稀疏的算法的出现，因此没有遵循此过程。

数值稳定性

w:数值稳定性在这个过程中可能是一个问题，并且有各种方法可以克服这种不稳定性。最基本且普遍适用的方法之一称为F混合或阻尼。使用F混合，一旦计算出一个单电子波函数，它就不会直接使用。相反，使用该计算波函数与之前该电子的波函数的某种组合，最常见的是计算波函数和紧接其前的波函数的简单线性组合。Hartree在原子计算中采用的一个巧妙的策略是增加核电荷，从而将所有电子拉得更近。随着系统的稳定，逐渐将其减少到正确的电荷。在分子计算中，有时通过首先计算正离子的波函数，然后使用这些轨道作为中性分子的起点，来使用类似的方法。现代分子Hartree-Fock计算机程序使用多种方法来确保Roothaan-Hall方程的收敛。

弱点、扩展和替代方案

在“Hartree-Fock算法”部分概述的五个简化中，第五个通常是最重要的。忽略电子相关性会导致与实验结果出现较大偏差。为了将电子相关性包含到多电子波函数中，人们设计了许多方法来克服这种弱点，这些方法统称为w:后Hartree-Fock方法。其中一种方法，w:Møller-Plesset微扰理论，将相关性视为Fock算符的微扰。其他方法将真正的多电子波函数展开为Slater行列式的线性组合，例如w:多组态自洽场、w:组态相互作用、w:二次组态相互作用和完全活性空间自洽场 (CASSCF)。还有一些其他方法（例如变分量子蒙特卡罗）通过将Hartree-Fock波函数乘以相关函数（“Jastrow”因子）来修改Hartree-Fock波函数，该项明确地是多个电子的函数，不能分解成独立的单粒子函数。

在某些情况下，Hartree-Fock计算的一种替代方法是w:密度泛函理论，它处理交换和相关能量，尽管是近似地。实际上，通常使用两种方法的混合计算，流行的B3LYP方案就是一种这样的w:混合泛函方法。另一个选择是使用w:现代价键方法。

软件包

有关已知处理Hartree-Fock计算（特别是针对分子和固体）的软件包列表，请参见w:量子化学和固态物理软件列表.

来源

• Levine, Ira N. (1991). Quantum Chemistry (第 4 版). 新泽西州英格伍德悬崖: 普伦蒂斯·霍尔. pp. 455–544. ISBN 0-205-12770-3.
• Cramer, Christopher J. (2002). Essentials of Computational Chemistry. 奇切斯特: 约翰·威利父子公司. pp. 153–189. ISBN 0-471-48552-7.
• Szabo, A.; Ostlund, N. S. (1996). Modern Quantum Chemistry. 纽约米尼奥拉: 多佛出版公司. ISBN 0-486-69186-1.

Slater 行列式

双粒子情况

近似多粒子系统波函数的最简单方法是取适当选择的正交个体粒子波函数的乘积。对于具有空间坐标$\mathbf {x} _{1}$和$\mathbf {x} _{2}$的两个粒子情况，我们有

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2})=\chi _{1}(\mathbf {x} _{1})\chi _{2}(\mathbf {x} _{2}).$

该表达式在w:Hartree-Fock方法中用作多粒子波函数的w:假设，被称为w:Hartree乘积。然而，它对于w:费米子并不令人满意，因为上述波函数不是反对称的，而它必须是w:费米子根据w:泡利不相容原理的要求。反对称波函数可以用数学方式描述如下

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2})=-\Psi (\mathbf {x} _{2},\mathbf {x} _{1})$

这对于Hartree乘积不成立。因此，Hartree乘积不满足泡利原理。这个问题可以通过对两个Hartree乘积进行w:线性组合来克服

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2})={\frac {1}{\sqrt {2}}}\{\chi _{1}(\mathbf {x} _{1})\chi _{2}(\mathbf {x} _{2})-\chi _{1}(\mathbf {x} _{2})\chi _{2}(\mathbf {x} _{1})\}$

$={\frac {1}{\sqrt {2}}}{\begin{vmatrix}\chi _{1}(\mathbf {x} _{1})&\chi _{2}(\mathbf {x} _{1})\\\chi _{1}(\mathbf {x} _{2})&\chi _{2}(\mathbf {x} _{2})\end{vmatrix}}$

其中系数是w:归一化因子。此波函数现在是反对称的，不再区分费米子，也就是说：无法为特定粒子指定序数，给定的索引是可以互换的。此外，如果两个费米子的任何两个波函数相同，它也将变为零。这相当于满足泡利不相容原理。

泛化

该表达式可以推广到任意数量的费米子，方法是将其写成w:行列式。对于一个N电子系统，Slater行列式定义为

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{N})={\frac {1}{\sqrt {N!}}}\left|{\begin{matrix}\chi _{1}(\mathbf {x} _{1})&\chi _{2}(\mathbf {x} _{1})&\cdots &\chi _{N}(\mathbf {x} _{1})\\\chi _{1}(\mathbf {x} _{2})&\chi _{2}(\mathbf {x} _{2})&\cdots &\chi _{N}(\mathbf {x} _{2})\\\vdots &\vdots &\ddots &\vdots \\\chi _{1}(\mathbf {x} _{N})&\chi _{2}(\mathbf {x} _{N})&\cdots &\chi _{N}(\mathbf {x} _{N})\end{matrix}}\right|\equiv \left|{\begin{matrix}\chi _{1}&\chi _{2}&\cdots &\chi _{N}\\\end{matrix}}\right|,$

在最后的表达式中，引入了一种紧凑的记号：归一化常数和费米子坐标的标签被理解 - 只有波函数被展示出来。对于双粒子情况，哈特里乘积的线性组合可以清楚地看作与N = 2 的斯莱特行列式相同。可以看出，使用斯莱特行列式确保从一开始就得到一个反对称函数；对称函数被自动拒绝。同理，使用斯莱特行列式确保符合w:泡利不相容原理。事实上，如果集合{χ_i} 是w:线性相关的，则斯莱特行列式为零。特别地，当两个（或更多）自旋轨道相同时，情况就是这样。在化学中，人们用这句话来表达这个事实，即不能有两个电子占据相同的自旋轨道。通常，斯莱特行列式通过w:拉普拉斯展开进行计算。在数学上，斯莱特行列式是一个反对称张量，也称为w:外积。

在w:哈特里-福克理论中，单个斯莱特行列式被用作电子波函数的近似。在更精确的理论（如w:组态相互作用和w:多组态自洽场）中，需要斯莱特行列式的线性组合。

S. F. Boys 提出用“detor”来描述一般类型的斯莱特行列式，但这个术语很少使用。

与受到泡利不相容原理约束的w:费米子不同，两个或多个w:玻色子可以占据系统相同的量子态。描述相同w:玻色子系统的波函数在粒子交换下是对称的，并且可以用w:永年式来展开。

Fock矩阵

在w:哈特里-福克方法中，Fock矩阵是近似于给定量子系统在一组给定的基向量中单电子w:能量算符的矩阵。

它最常在尝试解决原子或分子系统的w:Roothaan方程时在w:计算化学中形成。Fock矩阵实际上是量子系统真实哈密顿量算符的近似。它包括电子-电子排斥的影响，但只是以平均的方式。重要的是，由于Fock算符是一个单电子算符，它不包括w:电子相关能量。

Fock矩阵由Fock算符定义。对于假设w:闭壳轨道和单行列式波函数的限制情况，第i个电子的Fock算符由下式给出：

${\hat {F}}(i)={\hat {h}}(i)+\sum _{j=1}^{n/2}[2{\hat {J}}_{j}(i)-{\hat {K}}_{j}(i)]$

其中

${\hat {F}}(i)$ 是系统中第i个电子的Fock算符，

${\hat {h}}(i)$ 是第i个电子的w:单电子哈密顿量，

$n$ 是电子的数量，${\frac {n}{2}}$ 是闭壳系统中占据轨道的数量，

${\hat {J}}_{j}(i)$ 是w:库仑算符，定义了系统中第j个和第i个电子之间的排斥力，

${\hat {K}}_{j}(i)$ 是w:交换算符，定义了交换两个电子时产生的量子效应。

库仑算符乘以2，因为每个占据轨道上有两个电子。交换算符不乘以2，因为它只有在电子自旋与第i个电子相同的情况下才会有非零结果。

对于具有不成对电子的体系，福克矩阵有很多选择。

Hartree-Fock (HF) 或自洽场 (SCF)

密度泛函理论

与量子态对称性的关系

具有单值多粒子波函数的泡利不相容原理等同于要求波函数反对称。反对称的双粒子态表示为态的叠加，其中一个粒子处于$\scriptstyle |x\rangle$态，另一个粒子处于$\scriptstyle |y\rangle$态。

$|\psi \rangle =\sum _{x,y}A(x,y)|x,y\rangle$

交换后的反对称性意味着A(x,y) = −A(y,x)。这意味着A(x,x) = 0，这就是泡利不相容原理。这在任何基底中都是成立的，因为幺正基底变换会保持反对称矩阵的反对称性，虽然严格来说，A(x,y) 不是矩阵，而是反对称的二阶w:张量。

反之，如果对角量A(x,x)在每个基底中都为零，那么波函数分量

$A(x,y)=\langle \psi |x,y\rangle =\langle \psi |(|x\rangle \otimes |y\rangle )$

必然是反对称的。为了证明这一点，考虑矩阵元

$\langle \psi |((|x\rangle +|y\rangle )\otimes (|x\rangle +|y\rangle ))\,$

这是零，因为两个粒子同时处于叠加态$\scriptstyle |x\rangle +|y\rangle$的概率为零。但它等于

$\langle \psi |x,x\rangle +\langle \psi |x,y\rangle +\langle \psi |y,x\rangle +\langle \psi |y,y\rangle \,$

右侧的第一项和最后一项是对角元素，为零，整个和为零。所以波函数矩阵元服从

$\langle \psi |x,y\rangle +\langle \psi |y,x\rangle =0\,$.

或

$A(x,y)=-A(y,x)\,$

泡利原理在高级量子理论中的应用

根据w:自旋统计定理，自旋为整数的粒子占据对称量子态，而自旋为半整数的粒子占据反对称态。此外，根据量子力学原理，自旋值只能为整数或半整数。在相对论w:量子场论中，泡利原理来自于对半整数自旋粒子施加虚时间旋转算符。由于在非相对论情况下，粒子可以具有任何统计特性和任何自旋，因此无法在非相对论量子力学中证明自旋统计定理。

在一维空间中，玻色子和费米子都可以遵守不相容原理。具有无限强度的德尔塔函数排斥相互作用的一维玻色气体等效于自由费米子气体。造成这种情况的原因是，在一维空间中，粒子的交换要求它们彼此穿过；对于无限强的排斥力，这种情况不可能发生。这种模型由量子w:非线性薛定谔方程描述。在动量空间中，不相容原理也适用于具有德尔塔函数相互作用的玻色气体中的有限排斥力， 以及对于相互作用自旋和w:哈伯德模型在一维空间中，以及对于其他可以通过w:贝特假设求解的模型。通过贝特假设求解的模型中的基态是一个费米球。

密度泛函理论

参考文献

另请参阅有关如何添加参考文献的编辑本书说明w:纳米技术/关于#如何贡献。

---

Hartree–Fock 方法