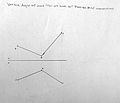
描述几何/圆锥轨迹

定义

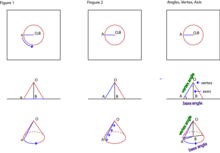
轨迹（locus/loci）是满足给定条件的一组解。[[[[Media:|thumbnail]]]] 根据具体情况，轨迹可以是不同的解。在图A中，有一条垂直轴BO和一个点a。当点a绕BO旋转时，点a形成的路径是一个圆。在这个给定的条件下，轨迹是点a绕BO旋转时形成的圆形路径，因为这个圆是所有与BO的距离与点a相同的点的集合。在图B中，有一条垂直轴BO，线段AO与BO相交形成∠AOB。当AO绕BO旋转时，AO形成的路径是一个锥形的表面。因此，在这个特定的条件下，轨迹AO是一个锥面，因为这个表面是三维空间中所有可以用AO表示的线段的集合。

两个相交物体的轨迹将是满足交点的所有解。如果圆锥“A”和圆锥“B”共享一个顶点并具有相同的母线长，则有三种可能的解：1个交点、2个交点或没有交点。如果两条轴之间的角度小于两个顶角之和，则有两个轨迹交点解。如果两条轴之间的角度等于两个顶角之和，则只有一个解。如果两条轴之间的角度大于两个顶角之和，则没有解。

求解圆锥轨迹交线

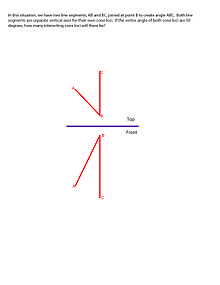
考虑两条相交线AO和BO的顶视图和正视图，夹角为∠AOB。由线绕AO和BO旋转（形成圆锥）形成的顶角分别为α和β。构造视图，使一个视图显示两个圆锥轴的真实长度（正视图），另一个视图显示两个圆锥轴的点视图（顶视图）。在真实长度视图中，构造一个任意半径的圆，使其与圆锥的母线相交。连接圆锥和圆的交点，形成圆锥的底面。标记每个圆锥底面与另一个圆锥底面相交的所有点。这些是圆锥交点的轨迹。从轨迹到顶点的线是每个圆锥与其相邻圆锥交汇的边缘。

如果圆锥的轴不是线段，而是无限长的直线，则需要测试是否存在两个以上的解。产生圆锥面的旋转线可以从顶点指向不同的方向，从而产生两个圆锥的可能性。因此，对于四个圆锥，最多可以有四个轨迹交点。