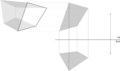
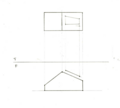
描述几何/距离

点到直线的距离

点和直线之间的真实距离是它们之间的最短距离。首先，沿平行于直线的折叠线投影辅助视图以找到其真实长度。确保也投影点。其次，沿垂直于直线的折叠线创建另一个辅助视图以找到它点视图。两点之间的距离是真实距离。

直线到直线的距离

平行线

平行线：通过沿平行折叠线投影它们来找到平行线的真实长度（找到其中一条线的真实长度将找到另一条线的真实长度）。接下来，通过制作垂直折叠线并再次投影直线来找到两条线的点视图。两点之间的距离是两条平行线之间的真实距离。

异面直线

异面直线：找到两条直线中的任何一条的真实长度，但仍然投影两条直线穿过折叠线。然后找到真实长度的直线的点视图。绘制一条垂直于直线的线，该线穿过该点，这是异面直线之间的距离。

直线到平面的距离

为了找到直线和平面之间的距离，第一步是将直线放在点视图中。这可以通过创建一个垂直于真实长度的直线的折叠线并使用转移距离来构建视图来完成。

如果直线和平面平行，这种结构也会将平面放在边缘视图中。直线和平面之间的距离将是从点视图中的直线到边缘视图中的平面的直线的长度。边缘视图中的平面将显示为一条线，但它可以在任何方向无限延伸。

问题
解决方案

如果直线和平面不平行（即当直线处于点视图时，平面不处于边缘视图），那么直线将与平面在某一点相交，距离为零。您可以通过找到平面在边缘视图中的位置并看到直线最终将刺穿平面来验证这一点。

问题
解决方案

与水平线成一定角度的距离，应用于线段

找到与水平线成一定角度的距离涉及到找到两个点之间的距离，这两个点不共享垂直于视点方向的平面。为了找到这个距离，首先要将这两个给定点用一条线段连接起来。然后，首先在点视图中构建该线，以便可以将其构建为真实长度，从而给出两点之间的真实距离。

图示说明如何在空间中构建两点之间的距离。

示例问题

气象站 A 位于海拔 3250 米的山上。气象站 B 位于距离气象站 A 10 公里的海拔 4500 米的山峰上。气象局有兴趣将这两个站与海拔 7000 米的气象气球结合起来用作三角测量装置。气象气球必须放置在使它完成等边三角形的位置。气象局可以在哪里放置气球，气球与每个气象站之间的距离是多少？

示例问题的解决方案

点到立体的距离

在这种情况下，找到点到立体的最短距离意味着找到给定点和最靠近该立体的最近面的最近点之间的最短距离，假设该立体具有平面面。因此，在做这个问题时，将一个正在交互的元素隔离起来是有用的，在这种情况下，是最接近的面和正在考虑的点。这简化了找到点和平面之间的最短距离的问题。

为了找到点和平面之间的最短距离，首先必须找到平面在边缘视图中的视图。通过将平面显示在边缘视图中，人们进一步简化了问题，使其变为找到点和直线之间的最短距离。一旦你有了平面在边缘视图中的位置，你必须创建一个垂直于平面的直线。在将这条直线转移回先前的视图后，可以使用穿刺点结构来找到平面中最靠近给定点的点，因此是立体中最靠近给定点的点。

演示如何拆解立体，以便可以找到最靠近外部点的边的点。

示例问题

超级羊驼正在逃避一立方千米邪恶的飞行恶魔宝宝，这些宝宝是来自短蛋糕博士。每个飞行的恶魔宝宝占据一立方米的空间。立方体的底部距离地面 2 公里，并且倾斜的方式使得四个边指向一个基点。如果短蛋糕博士在超级羊驼上空 10 公里，并且在超级羊驼的顶视图中距离立方体中心 8 公里，立方体中心位于超级羊驼的 N60 度 E 方向，那么哪个飞行恶魔宝宝会首先到达超级羊驼？

示例问题的解决方案

直线到立体的距离

为了求解直线到立体的最短距离，这个问题必须被视为求解直线到平面的最短距离。立体中最靠近该直线的面的应该被视为这个独立的平面。然后，该过程变得相当简单：您所要做的就是执行找到直线到平面的最短距离的构造（如上所述，它本身只是简化为找到点和直线之间的最短距离的构造）。

重申一下，找到直线到平面的最短距离的构造如下：首先必须构建一个视图，在该视图中，直线以点视图显示。如果直线和平面平行，则平面应该在直线以点视图显示的同一视图中以边缘视图显示（否则，直线和平面最终将相交，因此它们之间的最短距离为零，如上所述）。然后所要做的就是用一条垂直线将点视图中的直线连接到平面的边缘视图。这条垂直线是真实长度，是直线和平面之间的最短距离，在这种情况下，这也意味着它是直线和立体之间的最短距离。如果需要，您可以通过使用转移距离将最短距离线投影到其他视图中。

如果实体是一个圆形面的实体，例如圆柱体，要找到直线和实体之间的最短距离，可以将实体抽象为一条直线——其中心线——并使用查找直线和点之间最短距离的构造方法。你只需要将实体的厚度，即实体的直径加回到最终视图中，就可以得到实体和直线之间的实际比例距离。

示例问题

一座著名的意大利钟楼面临倒塌的危险。在图纸中，它被近似地表示为一个斜圆柱。为了支撑钟楼，工程师们在钟楼旁边的地面上放置了一个倾斜的支架，现在他们想用钢索连接钟楼和支架。为了开始，工程师们想知道连接钟楼和支架的钢索的最短长度是多少；换句话说，他们想知道钟楼和支架之间的最短距离是多少。找到这个距离。使用 1 毫米等于 5 英尺的比例；钟楼的半径是 10 英尺（2 毫米）。

示例问题

解决方案：为了解决这个问题，你只需要将圆柱体的中心线视为一条直线，然后使用上面描述的查找点和直线之间最短距离的构造方法。

示例问题的解决方案

从平面到实体的距离

平面和实体之间的最短距离可以通过将实体离平面最近的面视为一个独立的平面来找到。这样，问题就简化为找到两个平面之间的最短距离，这就是你必须进行的构造，以找到原始平面和实体之间的最短距离。再次强调，为了进行这种构造，两个平面必须平行，否则它们最终会相交，使它们之间的最短距离为零。

查找两个平面之间最短距离的构造最终简化为查找直线和平面之间的最短距离。你必须首先创建一个视图，在这个视图中，两个平面都以边缘视图显示，由于平面是平行的，这意味着只需要创建一个平面上的边缘视图。然后，你可以在其中一条边缘视图线路上选择一个任意点，从该点可以画一条垂直线到另一条边缘视图线上。这条直线处于真实长度，是两个平面之间的最短距离。为了将最短距离线投射到其他视图，你必须执行穿刺点构造，以找到最短距离线与平面相交的点。

示例问题

一位建筑师在他的建筑物的一侧屋顶上方放置了一个遮阳装置。遮阳装置平行于屋顶表面。连接遮阳装置和屋顶的支撑线的最短长度是多少（从遮阳装置平面到实体屋顶表面的最短距离）？

如何找到平行于彼此的平面和实体表面的最短距离的示例问题

解决方案：这个问题有点像一个陷阱问题。它测试你对推动问题概念的理解程度。在这种情况下，平面与实体的最近面均匀平行。实体的正面已经显示在正面视图中的真实形状，因为它与正面视图和顶视图中的折叠线平行。这意味着平面在正面视图中的边缘视图以真实长度显示，因为它与实体正面中的一个侧面平行。由于所有这一切都是正确的，这意味着从平面到实体最近表面的最短距离在从平面到表面的所有垂线上都是一样的。因此，从平面到表面的最短距离已经隐含地显示在该正面视图中；如果你愿意，你只需要测量那个距离。

示例问题的解决方案

从实体到实体的距离

当求解两个实体之间的最短距离时，将两者都视为直线，使用直线到直线的方法。例如，取两个圆柱体或一个锥体，求解它们轴之间的最短距离。然后考虑实体的深度；从中心到实体表面的距离。