描述几何/直纹曲面
外观
< 描述几何
一个直纹曲面,也称为卷曲面 S,是由直线沿曲线移动而产生的。相比之下,平面曲面是由直线沿另一条直线移动而产生的。当曲面上的每个点都可以连接到曲面上的至少另一个点以构成直线时,就存在直纹曲面。
直纹曲面的例子包括
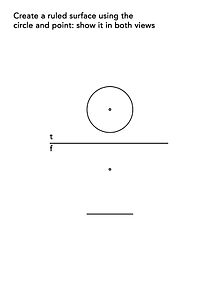
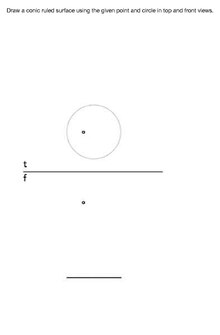
圆锥- 直线沿圆绕一点移动而产生的结果
"直圆锥" - 直线沿圆移动经过一点,该点直接位于圆心上方或下方。
"斜圆锥" - 直线沿圆移动经过一点,该点不直接位于圆心上方或下方。
"截头圆锥" - 直线沿圆移动经过一点,然后被平面或另一个实体截断。要完成视图,您将使用穿透点方法。(如果切割平面平行于直圆锥的底面,则结果是圆形。)
http://www.youtube.com/watch?v=SQZIKtObIIU
圆柱- 直线沿垂直于圆的圆移动。
"直圆柱" - 直线沿平行于垂直于圆平面轴线的圆移动而产生的结果。
"斜圆柱" - 直线沿圆移动,平行于不垂直于圆平面的轴线。
"截头圆柱" - 直线沿平行于轴线的圆移动,然后被另一个平面或实体截断。要完成视图,您将使用拼合点方法。
(如果切割平面平行于轴线,则结果是平行四边形。)
http://www.youtube.com/watch?v=L-lPkWvlUYc
现实生活中的例子
-
DNA 双螺旋
过山车- 平行轨道沿着过山车弯曲的结果移动。
直纹曲面的应用:在描述几何中,直纹曲面用于解决交点问题。当您将曲面(例如圆锥或圆柱的外部)视为一系列直线时,您将能够更容易地找到交点。
带有答案的示例问题