数字电路/加法器

半加器

考虑将两个二进制数加在一起

我们看到，“二进制”列中的位是在进位时生成的。半加器是一个电路，它将两个位加在一起并输出这两个位的总和。半加器有两个输出：和和进位。和表示 A+B/2 的整数除法的余数，而进位是结果。这可以表示如下

• ${\mbox{S}}=A\oplus B$
• ${\mbox{C}}=AB\,$

A B A+B S C 0 0 0 0 0 0 1 1 1 0 1 0 1 1 0 1 1 2 0 1

全加器

半加器有一个主要的局限性，即它们不能接受来自前一级的进位位，这意味着它们不能连接在一起以添加多位数。但是，半加器的两个输出位也可以表示结果 A+B=3，因为和和进位都为高电平。

因此，全加器可以接受三个位作为输入。通常，一位被称为进位输入位。全加器可以级联在一起，通过将一个输出的进位连接到下一个输入的进位，来产生任意位数的加法器。

A B Cin A+B+Cin S Cout 0 0 0 0 0 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 2 0 1 1 0 0 1 1 0 1 0 1 2 0 1 1 1 0 2 0 1 1 1 1 3 1 1

全加器通常显示为一个单元。和输出通常在块的底部，进位输出在左侧，因此这些设备可以连接在一起，最高有效位在最左边

行波进位加法器

行波进位加法器只是几个串联连接的全加器，因此进位必须通过每个全加器才能完成加法。行波进位加法器在所有加法器中需要的硬件最少，但它们是最慢的。

下图显示了一个四位加法器，它将数字 A[3:0] 和 B[3:0] 以及一个进位输入加在一起，生成 S[3:0] 和进位输出。

全加器中的传播延迟

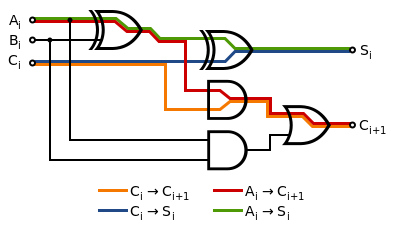
真正的逻辑门不会对输入做出瞬时反应，因此数字电路具有最大速度。通常，数字电路的延迟以门延迟来衡量，因为这使得可以为不同的器件计算设计的延迟。与门和或门具有名义上的 1 门延迟，异或门具有 2 门延迟，因为它们实际上是由与门和或门的组合组成的。

全加器块具有以下最坏情况传播延迟

• 从 A_i 或 B_i 到 C_i+1：4 门延迟（异或 → 与 → 或）
• 从 A_i 或 B_i 到 S_i：4 门延迟（异或 → 异或）
• 从 C_i 到 C_i+1：2 门延迟（与 → 或）
• 从 C_i 到 S_i：2 门延迟（异或）

因为一级门的进位输出是下一级的输入，所以最坏情况传播延迟是

• 从生成第一个进位信号（A₀/B₀ → C₁）开始的 4 门延迟。
• 每个中间阶段（C_i → C_i+1）的 2 门延迟。
• 在最后一个阶段产生和和进位输出（C_n-1 → C_n 和 S_n-1）的 2 门延迟。

因此，对于一个 n 位加法器，我们有一个总传播延迟，t_p 为

$t_{p}=4+2(n-2)+2=2n+2$

这与 n 成线性关系，对于一个 32 位数，需要 66 个周期才能完成计算。这相当慢，并且在一定程度上限制了我们设备的字长。我们想要找到加速它的方法。

先行进位加法器

一种快速加数的方法称为先行进位。这种方法不需要进位信号逐级传播，从而造成瓶颈。相反，它使用额外的逻辑来加速进位信息的传播和生成，以更少的硬件成本实现快速加法。

在行波加法器中，每个阶段都会比较进位输入信号，C_i，与输入 A_i 和 B_i，并相应地生成进位输出信号 C_i+1。在先行进位加法器中，我们定义了两个新的函数。

生成函数，G_i，指示如果不存在进位输入信号，该阶段是否会生成进位输出信号 C_i。如果两个加数在该位上都包含 1，则会发生这种情况

$G_{i}=A_{i}\cdot B_{i}\,$

传播函数，P_i，指示是否将该阶段的进位输入传递到该阶段的进位输出。如果两个加数中的任何一个在该位上包含 1，则会发生这种情况

$P_{i}=A_{i}+B_{i}\,$

请注意，这两个值都可以在单个门延迟的恒定时间内从输入中计算出来。现在，如果该阶段生成进位（G_i = 1）或存在进位输入并且该阶段传播进位（P_i·C_i = 1），则该阶段的进位输出发生

$C_{i+1}=A_{i}B_{i}+A_{i}C_{i}+B_{i}C_{i}\,$

$C_{i+1}=A_{i}B_{i}+(A_{i}+B_{i})C_{i}\,$

$C_{i+1}=G_{i}+P_{i}C_{i}\,$

下表总结了这一点

Ai	Bi	Ci		Gi	Pi	Ci+1
0	0	0		0	0	0
0	0	1		0	0	0
0	1	0		0	1	0
0	1	1		0	1	1
1	0	0		0	1	0
1	0	1		0	1	1
1	1	0		1	1	1
1	1	1		1	1	1

我们可以通过代入前一级的进位表达式来扩展进位表达式

$c_{i+1}=G_{i}+P_{i}c_{i}\,$

$c_{i+1}=G_{i}+P_{i}\left(G_{i-1}+P_{i-1}c_{i-1}\right)\,$

$c_{i+1}=G_{i}+P_{i}G_{i-1}+P_{i}P_{i-1}\left(G_{i-2}+P_{i-2}c_{i-2}\right)\,$

$c_{i+1}=\quad \vdots$

$c_{i+1}=G_{i}+P_{i}G_{i-1}+P_{i}P_{i-1}G_{i-2}+P_{i}P_{i-1}P_{i-2}G_{i-3}+\ldots +P_{i}P_{i-1}\cdots P_{1}P_{0}c_{0}\,$

注意，这不需要来自先前级的进位信号，因此我们不必等待更改在电路中级联传播。事实上，一旦传播和生成信号准备就绪，给定级的进位信号就可以用另外两个门延迟（一个与门和一个或门）计算出来。因此，给定级的进位可以在恒定时间内计算出来，因此和也可以在恒定时间内计算出来。

操作	所需数据	门延迟
生成级生成和传播信号	加数 (a 和 b)	1
生成级进位信号，C1 到 Cn	P 和 G 信号，以及 C0	2
生成和结果，S	进位信号和加数	3
总计		6

S、P 和 G 信号均由称为“部分全加器”（PFA）的电路生成，该电路类似于全加器。

请注意，虽然在上面的电路图中，P 信号被生成为了 A OR B，但另一个有效的选择是 A XOR B，优势在于 A XOR B 已经在电路图中出现，不需要额外的门。这是因为在公式 $C_{i+1}=G_{i}+P_{i}C_{i}$ 中，$P_{i}$ 的实现方式并不重要，因为 $AB+(A+B)C$ 和 $AB+(A\oplus B)C$ 是等效的表达式，读者可以使用真值表进行验证。

为了构建一个稍微小一点的电路，传播信号可以从第一个 XOR 门的输出端获取，而不是使用专门的 OR 门，因为如果 A 和 B 都被断言，生成信号将强制产生进位。然而，这种简化意味着传播信号需要两个门延迟才能产生，而不仅仅是一个门延迟。

进位超前加法器包含 n 个 PFA 和用于从级传播和生成信号产生进位的逻辑。

因此，两个数字可以在恒定时间内加起来，即 O(1)，只需要 6 个门延迟，与数字的长度 n 无关。然而，这需要具有高达 n 个输入的 AND 和 OR 门。如果逻辑门只有有限数量的输入，则需要构建树来计算这些输入，而总的计算时间是对数的，即 O(ln(n))，这仍然比波纹加法器的线性时间好得多。

级联进位超前加法器

基本进位超前加法器速度非常快，但缺点是它需要大量的逻辑硬件来实现。事实上，所需的硬件量大约与 n 的平方成正比，并且当 n 大于 4 时开始变得非常复杂。

因此，大多数 CLA 由包含 4 位 CLA 的“块”构成，这些块被级联起来以产生更大的 CLA。

进位保留加法器

进位保留加法器是一种传播延迟（关键路径）较低的加法器，但它不是将两个输入数字加到一个输出和，而是将三个输入数字加到一对输出数字。当它的两个输出然后被一个传统的进位超前加法器或波纹进位加法器相加时，我们得到所有三个输入的和。

在将三个或更多个数字加在一起时，以单个进位超前加法器结尾的一系列进位保留加法器比一系列进位超前加法器提供了更好的传播延迟。特别是，进位保留加法器的传播延迟不受被加向量的宽度影响。

进位保留加法器实际上是完全并行的全加器电路阵列，三个输入向量的每个位都加载到每个全加器的 A、B 和 Cin 输入。每个全加器的输出 S 连接到一个输出的相应输出位，它的输出 Cout 连接到第二个输出的下一个更高的输出位；第二个输出的最低位直接从进位保留的 Cin 输入馈送。

本节的 数字电路 维基教科书是一个 存根。您可以通过扩展本节来帮助我们。如果您添加了一些内容，请将自己列为 贡献者。