数字电路/CORDIC

一个 CORDIC (代表 **CO**ordinate **R**otation **DI**gital **C**omputer) 电路用于计算一些常见的数学函数，例如三角函数、双曲函数、对数函数和指数函数。

应用

CORDIC 只使用加法器和位移来计算结果，因此它可以使用相对基本的硬件实现。

像幂级数或查表法通常需要执行乘法。如果硬件乘法器不可用，CORDIC 通常更快，但如果可以使用乘法器，其他方法可能更快。

CORDIC 可以用多种方法实现，包括单级迭代方法，与乘法器电路相比，它需要很少的门。此外，CORDIC 可以使用完全相同的硬件计算许多函数，因此它们非常适合那些将降低成本（例如通过减少 FPGA 中的门数）优先于速度的应用。这种优先级的一个例子是袖珍计算器，其中 CORDIC 被广泛使用。

历史

CORDIC 最初是由 J.E. Volder 于 1959 年在康维尔航空电子部门发明的，它被设计用于 B-58 轰炸机的导航计算机，以取代模拟分解器，一种计算三角函数的设备（圆 CORDIC）。

1971 年，惠普的 J.S. Walther 将该方法扩展到计算双曲函数、自然对数、自然指数、乘法、除法和平方根（线性 CORDIC 和双曲 CORDIC）。

2019 年，基于双曲 CORDIC，罗元勇等人进一步提出了一种广义双曲 CORDIC (GH CORDIC) 来直接计算具有任意固定基数的对数和指数。理论上，双曲 CORDIC 是 GH CORDIC 的特例。

通用概念

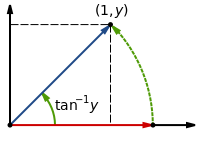
考虑以下向量的旋转

从 (1, 0) 开始 旋转 θ 我们得到 (cosθ, sinθ)	从 (1, y) 开始 旋转直到 y = 0 旋转是 tan−1y

如果我们有一个计算效率高的向量旋转方法，我们可以直接计算正弦、余弦和反正切函数。但是，任意角度的旋转并不容易（你必须知道正弦和余弦，而这正是我们所没有的）。我们使用两种方法来简化它

• 我们不执行旋转，而是执行“伪旋转”，它们更容易计算。
• 用一组特殊角度 α_i 的和来构造所需的角度 θ

$\theta =\alpha _{1}+\alpha _{2}+\ldots +\alpha _{m}$

下图显示了长度为 R_i 的向量绕原点旋转 a_i 角的旋转和伪旋转

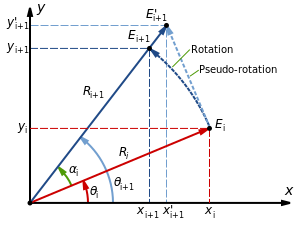
绕原点旋转产生以下坐标

$x_{i+1}=x_{i}\cos \alpha _{i}-y_{i}\sin \alpha _{i}$

$y_{i+1}=y_{i}\cos \alpha _{i}+x_{i}\sin \alpha _{i}$

$\theta _{i+1}=\theta _{i}+\alpha _{i}$

回想一下身份 $\cos \theta \equiv 1{\Big /}{\sqrt {1+\tan ^{2}\theta }}$.

$x_{i+1}=\left(x_{i}-y_{i}\tan \alpha _{i}\right){\Big /}{\sqrt {1+\tan ^{2}\alpha _{i}}}$

$y_{i+1}=\left(y_{i}+x_{i}\tan \alpha _{i}\right){\Big /}{\sqrt {1+\tan ^{2}\alpha _{i}}}$

我们的策略是消除因子 $1{\Big /}{\sqrt {1+\tan ^{2}\alpha _{i}}}$，并设法消除乘以 $\tan \alpha _{i}$。伪旋转生成一个与旋转向量具有相同角度但长度不同的向量。事实上，伪旋转将长度更改为

$R_{i+1}={\frac {R_{i}}{\cos \alpha _{i}}}=R_{i}{\sqrt {1+\tan ^{2}\alpha _{i}}}$

因此，我们现在有以下伪旋转后的坐标

$x_{i+1}^{\prime }=\left(x_{i}-y_{i}\tan \alpha _{i}\right)$

$y_{i+1}^{\prime }=\left(y_{i}-x_{i}\tan \alpha _{i}\right)$

$\theta _{i+1}=\theta _{i}-\alpha _{i}$

伪旋转成功地消除了我们的长度因子，而长度因子本来需要一个代价高昂的除法运算。然而，向量将在n个伪旋转序列中增长K倍

$K=\prod _{i=0}^{n-1}{\sqrt {1+\tan ^{2}\alpha _{i}}}$

然后，经过n个伪旋转后的坐标为

$x_{n}=K\left(x_{i}\cos \sum _{i=0}^{n-1}{\alpha _{i}}-y_{i}\sin \sum _{i=0}^{n-1}\alpha _{i}\right)$

$y_{n}=K\left(y_{i}\cos \sum _{i=0}^{n-1}{\alpha _{i}}+x_{i}\sin \sum _{i=0}^{n-1}\alpha _{i}\right)$

$\theta _{n}=\theta _{i}-\sum _{i=0}^{n-1}{\alpha _{i}}$

前三次伪旋转。注意我们如何收敛到正确的角度，θ

如果角度总是相同的集合，那么 K 是固定的，可以在以后考虑。我们根据两个标准选择这些角度

• 我们还必须选择角度，以便任何角度都可以通过所有角度的总和来构建，并带有适当的符号。
• 我们将所有 $\tan \alpha _{i}$ 设置为 2 的幂，以便乘法可以通过二进制数的简单逻辑移位来执行。

正切函数在区间 [0, π/2] 上具有单调递增的梯度，因此给定角度的正切始终小于该角度的一半正切的两倍。这意味着如果我们使角度 $\alpha _{i}=\tan ^{-1}2^{-i}$，我们可以满足这两个标准。请注意，正切函数是奇函数，这意味着要以另一种方式进行伪旋转，您只需减去而不是添加角度的正切。

i	αi = tan−1 (2−i)
	度	弧度
0	45.00	0.7854
1	26.57	0.4636
2	14.04	0.2450
3	7.13	0.1244
4	3.58	0.0624
5	1.79	0.0312
6	0.90	0.0160
7	0.45	0.0080
8	0.22	0.0040
9	0.11	0.0020

在过程的步骤 i 中，我们以 $d_{i}2^{-i}\,$ 进行伪旋转，其中 $d_{i}\,$ 是旋转的方向（或符号），这将在每一步都选择，以迫使角度收敛到所需的最终旋转。例如，考虑 28° 的旋转

$28\approx 45.0-26.57+14.04-7.13+3.58-1.79+0.90-0.45+0.22+0.11$

$28\approx 27.91$

我们采取的步骤越多，我们就可以通过连续旋转来进行更好的近似。因此，我们有以下迭代坐标计算

$x_{i+1}=x_{i}-d_{i}y_{i}2^{-i}$

$y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$

$\theta _{i+1}=\theta _{i}-d_{i}\alpha _{i}$

为了达到k位的精度，需要进行k次迭代，因为$\tan ^{-1}2^{-i}\lessapprox 2^{-i}$，随着i的增加而收敛。

使用CORDICs

CORDICs可以用来计算许多函数。一个CORDIC有三个输入，x₀, y₀和z₀。根据CORDIC的输入，可以在输出x_n, y_n和z_n产生不同的结果。

在旋转模式下使用CORDIC

$x_{i+1}=x_{i}-d_{i}y_{i}2^{-i}$ $y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$ $z_{i+1}=z_{i}-d_{i}\alpha _{i}$

$x_{n}=K\left(x_{0}\cos z_{0}-y_{0}\sin z_{0}\right)$ $y_{n}=K\left(y_{0}\cos z_{0}+x_{0}\sin z_{0}\right)$ $z_{n}=0$

为了使z_n收敛到0，选择$d_{i}={\mbox{sgn }}z_{i}$.

如果我们从x₀ = 1/K和y₀=0开始，在过程结束时，我们会发现x_n=cos z₀和y_n=sin z₀。

收敛域是$-99.7^{\circ }<z_{0}<99.7^{\circ }$，因为99.7°是列表中所有角度的总和。

在矢量模式下使用CORDIC

$x_{i+1}=x_{i}-d_{i}y_{i}2^{-i}$ $y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$ $z_{i+1}=z_{i}-d_{i}\alpha _{i}$

$x_{n}=K{\sqrt {x^{2}+y^{2}}}$ $y_{n}=0$ $z_{n}=z_{0}+\tan ^{-1}\left(y_{0}/x_{0}\right)$

为了使y_n收敛到0，选择$d_{i}=-{\mbox{sgn }}(y_{i})$.

如果我们从x₀ = 1和z₀ = 0开始，我们会发现z_n=tan⁻¹y₀

CORDICs的实现

位并行，展开

位并行，迭代

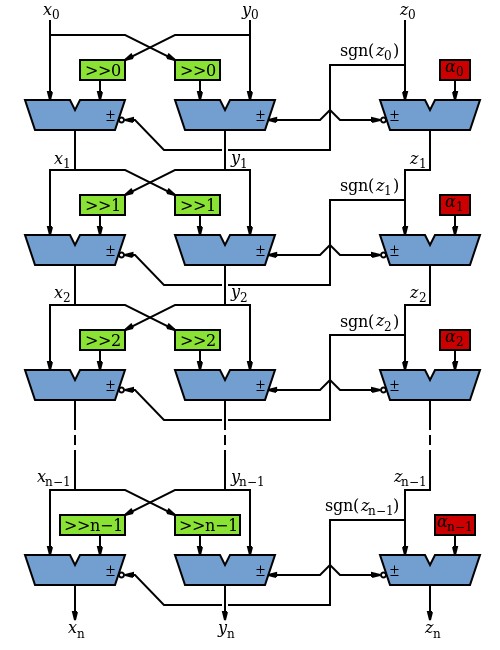
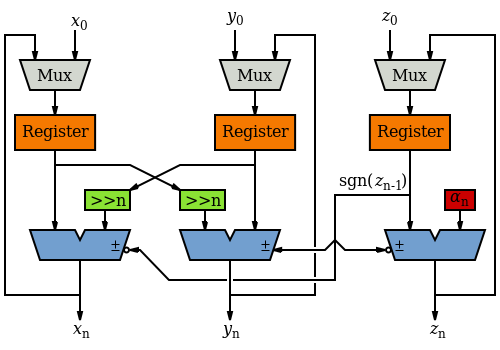
如果不需要高速，可以使用一个加法器和一个移位器实现。

通用 CORDIC

通过引入因子μ，我们也可以满足线性函数和双曲函数的需求。

$x_{i+1}=x_{i}-\mu d_{i}y_{i}2^{-i}$

$y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$

$z_{i+1}=z_{i}-d_{i}\alpha _{i}$

通用 CORDIC 实现的总结

$x_{i+1}=x_{i}-\mu d_{i}y_{i}2^{-i}$

$y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$

$z_{i+1}=z_{i}-d_{i}\alpha _{i}$

模式	旋转	矢量化
	$d_{i}={\mbox{sgn }}(z_{i}),\quad z\rightarrow 0$	$d_{i}=-{\mbox{sgn }}(y_{i}),\quad y\rightarrow 0$
圆形 μ = 1 αi = tan−12−i
线性 μ = 0 αi = 2−i
双曲 μ = -1 αi = tanh−12−i
在双曲模式下，需要重复第 4，13，40，121，...，j，3j+1，... 步。下面的常数K' 可以解释这一点。 K = 1.646760258121... 1/K = 0.607252935009... K' = 0.8281593609602... 1/K' = 1.207497067763...

直接可计算函数

$\sin z\,$	$\cos z\,$
$\tan ^{-1}z\,$	$\sinh z\,$
$\cosh z\,$	$\tanh ^{-1}z\,$
$y/x$	$xz$
$\tan ^{-1}(y/x)\,$	${\sqrt {x^{2}+y^{2}}}$
${\sqrt {x^{2}-y^{2}}}$	$e^{z}=\sinh z+\cosh z$

间接可计算函数

除了上述函数外，还可以通过组合先前计算结果来生成许多其他函数。

$\tan z={\frac {\sin z}{\cos z}}\,$	$\cos ^{-1}w=\tan ^{-1}{\frac {\sqrt {1-w^{2}}}{w}}$
$\tanh z={\frac {\sinh z}{\cosh z}}$	$\sin ^{-1}w=\tan ^{-1}{\frac {w}{\sqrt {1-w^{2}}}}$
$\ln w=2\tanh ^{-1}{\frac {w-1}{w+1}}$	$\log _{b}w={\ln w \over \ln b}$
$w^{t}=e^{t\ln w}$	$\cosh ^{-1}=\ln \left(w+{\sqrt {w^{2}-1}}\right)$
$\tan ^{-1}(y/x)\,$	$\sinh ^{-1}=\ln \left(w+{\sqrt {w^{2}+1}}\right)$
${\sqrt {x^{2}-y^{2}}}$	${\sqrt {w}}={\sqrt {(w+1/4)^{2}-(w-1/4)^{2}}}$

进一步阅读

• Volder, J.E. (1959), "CORDIC 三角函数计算技术" (PDF), IRE 电子计算机学报, 8 (3): 330–334, 检索于 2009-06-02
• Walther, J.S. (1971), "基本函数的统一算法" (w), 1971 年 5 月 18 日至 20 日春季联合计算机大会论文集: 379–385, 检索于 2009-06-02
• 罗元勇，王雨轩，哈亚军，王忠锋，陈思远，潘洪兵 (2019)，"广义双曲 CORDIC 及其任意固定基数的对数和指数计算"，IEEE 超大规模集成电路 (VLSI) 系统汇刊，27 (9): 2156–2169，doi:10.1109/TVLSI.2019.2919557 {{citation}}: |access-date= requires |url= (help)CS1 maint: multiple names: authors list (link)
• Vladimir Baykov，基于逐位 (CORDIC) 技术的基本函数评估问题，博士论文，列宁格勒国立电气工程大学，1972 年
• Schmid, Hermann，十进制计算。纽约，Wiley，1974 年
• V.D.Baykov，V.B.Smolov，计算机中基本函数的硬件实现，列宁格勒国立大学，1975 年，96 页。*全文
• Senzig, Don，计算器算法，IEEE Compcon 阅读摘要，IEEE 目录号 75 CH 0920-9C，第 139-141 页，IEEE，1975 年。
• V.D.Baykov，S.A.Seljutin，微型计算器中的基本函数评估，莫斯科，Radio & svjaz，1982 年，64 页。
• Vladimir D.Baykov，Vladimir B.Smolov，专用处理器：迭代算法和结构，莫斯科，Radio & svjaz，1985 年，288 页
• M. E. Frerking，通信系统中的数字信号处理，1994 年
• Vitit Kantabutra，关于计算指数和三角函数的硬件，IEEE 计算机汇刊 45 (3)，328-339 (1996)
• Andraka, Ray，基于 FPGA 计算机的 CORDIC 算法调查
• Henry Briggs，对数算术。伦敦，1624 年，对开本
• CORDIC 文献网站，王少云，2011 年 7 月
• 算法的秘密，Jacques Laporte，巴黎 1981 年
• 逐位方法，Jacques Laporte，巴黎 2006 年
• Ayan Banerjee，基于 CORDIC 的生物医学信号处理 FFT 处理器的 FPGA 实现，卡拉格浦尔，2001 年
• CORDIC 架构：综述，B. Lakshmi 和 A. S. Dhar，期刊：VLSI 设计，2010 年 1 月
• 在数字下变频器中实现 CORDIC 算法，C. Cockrum，2008 年秋季
• Parhami, B. (1999)，计算机算术：算法和硬件设计