数字电子学/逻辑与非门

逻辑与非门

与非门是两种基本逻辑门之一（另一种是与非门），任何其他逻辑门都可以用它们构建。由于这个特性，与非门和与非门有时被称为“通用门”。然而，现代集成电路并不是只由一种类型的门构建的。相反，EDA工具被用来将逻辑电路的描述转换为复杂门（标准单元）或晶体管（全定制方法）的网络列表。

组合逻辑门

非门

一个非门是由连接与非门的输入端来构成的。由于与非门等效于一个与门后跟一个非门，因此连接与非门的输入端只留下非门部分。

所需逻辑门	与非门构造
真值表 输入A 输出Q 0 1 1 0

与门

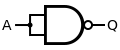
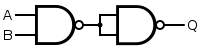
一个与门是由一个与非门后跟一个非门构成，如下所示。这相当于一个非与非，即与门。

所需逻辑门	与非门构造
真值表 输入A 输入B 输出Q 0 0 0 0 1 0 1 0 0 1 1 1

或门

如果检查与非门的真值表，或者应用德摩根定律，可以看到如果任何输入是0，那么输出将是1。但是，要成为一个或门，如果任何输入是1，输出也必须是1。因此，如果输入被反转，任何高输入将触发一个高输出。

所需逻辑门	与非门构造
真值表 输入A 输入B 输出Q 0 0 0 0 1 1 1 0 1 1 1 1

与非门

一个与非门仅仅是一个输出被反转的或门。

所需逻辑门	与非门构造
真值表 输入A 输入B 输出Q 0 0 1 0 1 0 1 0 0 1 1 0

异或门

一个异或门是由四个与非门连接构成，如下所示。这实际上表示公式：（A 与非 (A 与非 B)) 与非 (B 与非 (A 与非 B))。

所需逻辑门	与非门构造
真值表 输入A 输入B 输出Q 0 0 0 0 1 1 1 0 1 1 1 0

异或非门

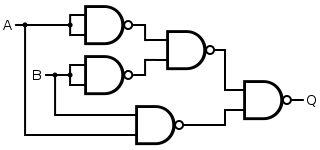
一个异或非门是用五个与非门构成。其中三个门以或门拓扑结构连接。这种排列的逻辑表达式为((A 或 B) 与非 (A 与非 B))。

所需逻辑门	与非门构造
真值表 输入A 输入B 输出Q 0 0 1 0 1 0 1 0 0 1 1 1

外部链接

• 使用逻辑门

参考文献

• Floyd, Thomas, L. (1997), 数字基础 (第6版), Englewood Cliffs, NJ: Prentice-Hall, ISBN 0133984885.