电和磁/静电学

仅仅通过摩擦不同的材料，比如头发和塑料，就可以产生电力。这会在两个摩擦的表面上产生大小相等但符号相反的电荷。然后我们可以观察到符号相反的电荷之间的吸引力和符号相同的电荷之间的排斥力。

库仑定律

两个静止的电荷之间施加的电力与其电荷乘积成正比，与其距离的平方成反比。这两个力，即 A 对 B 施加的力和 B 对 A 施加的力，都位于连接 A 和 B 中心线的方向上。这两个力在电荷符号相反时是吸引力，在电荷符号相同时是排斥力。

场是一个在空间中每个点每个时刻都可能变化的物理量。例如，温度就是一个场。库仑定律指出，一个静止的电荷 $q$ 会永久地在空间中产生一个电力场 $\mathbf {E}$

$\mathbf {E} (\mathbf {r} )=k_{e}{\frac {q}{r^{2}}}\mathbf {\hat {r}}$

其中 $\mathbf {r}$ 是从电荷 $q$ 到所考虑点的向量，$r$ 是它的长度，$\mathbf {\hat {r}} =\mathbf {r} /r$ 是 $\mathbf {r}$ 方向上的单位长度向量，$k_{e}={\frac {1}{4\pi \epsilon _{0}}}$ 是一个取决于测量单位选择的常数。

电力场 $\mathbf {E}$ 对电荷 $q'$ 施加的力是 $\mathbf {F} =q'\mathbf {E}$

所以电荷 $q$ 对电荷 $q'$ 的作用力是 ${\frac {1}{4\pi \epsilon _{0}}}{\frac {qq'}{r^{2}}}\mathbf {\hat {r}}$

场 $\mathbf {E}$ 就像一个计算一个电荷对另一个电荷作用力的数学中间量。但它远不止一个简单的数学中间量。它拥有独立存在的意义。麦克斯韦证明光是一种电磁波，即电磁场 ($\mathbf {E}$, $\mathbf {B}$) 的传播运动，而电场 $\mathbf {E}$ 是其中一个组成部分。

带正电球体表面的电场

两个电荷对第三个电荷的作用力是它们分别施加的作用力的总和。宇宙中所有电荷共同在空间中产生一个电场，它是每个电荷分别产生的电场的总和。

库仑力在数学上与万有引力相似：两个物体之间相互作用的万有引力与它们的质量乘积成正比，与它们之间距离的平方成反比。但万有引力总是吸引力，因为不存在负质量。在地球上，物体的重量就是地球对它的万有引力。

根据相对论，不存在瞬时超距作用。因此，一个电荷不能瞬时对另一个电荷施加库仑力。必须考虑力的传播时间。这就是为什么库仑定律只是静电学定律。它允许我们正确计算静止电荷之间的力。

物质的凝聚是静电性的

一粒小小的盐

每条线代表 NaCl 晶体中两个离子之间的键（氯化钠是食盐）。蓝色和绿色代表两种离子。它是一个体心立方晶体。每个 Na⁺ 离子周围有 8 个最近的 Cl^- 离子。同样，每个 Cl^- 离子周围有 8 个最近的 Na⁺ 离子。两个相邻离子总是带相反的电荷，因为异性电荷相互吸引，而同性电荷相互排斥。

解释固体、原子和分子凝聚力的力是库仑力。液体的凝聚也部分是由这种静电力引起的，但由于原子或分子在运动，因此电动力也可以起作用。

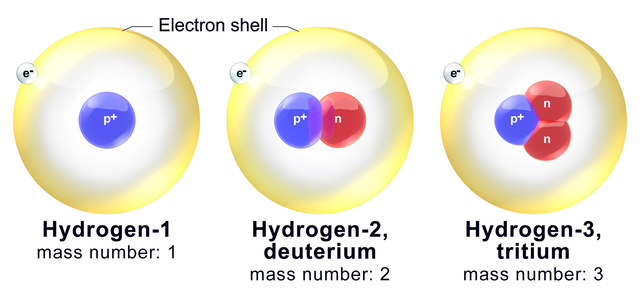
氢原子由一个质子、零个、一个或两个中子和一个电子组成。质子带正电。电子带负电，大小相等，符号相反。中子是中性的。电子通过库仑电力与质子相连。更一般地说，原子由一个原子核和核外电子组成。原子核的电荷为正，大小相等，符号相反于电子的总电荷。

当氢原子处于基态，即最低能量状态时，电子围绕质子的存在类似于一个球形云。

质子位于中心。周围的云代表电子的存在。

如果原子被激发，电子的存在可以有各种形式。

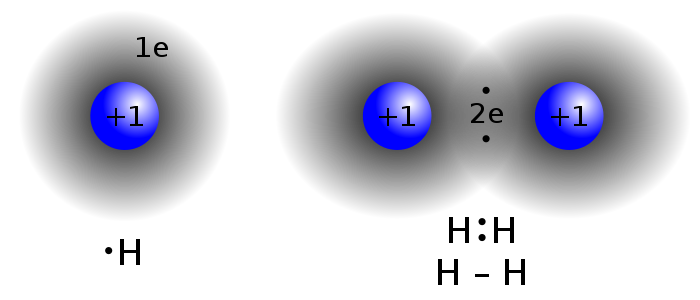
分子是原子组成的集合。电子就像将原子核粘合在一起的胶水。两个正电荷相互排斥，但两个正电荷被一个负电荷隔开可以相互吸引。

离子是指失去或获得一个或多个电子的原子或分子。由于原子和分子总是电中性的，因此离子总是带电的。失去一个或多个电子的原子或分子称为阴离子。获得一个或多个电子的原子或分子称为阳离子。

固体是由原子、分子或离子组成的集合，它们通过静电力相互连接。

要破坏离子晶体，必须分离由静电力吸引的离子。

异性电荷之间的吸引力大于同性电荷之间的排斥力。这种差异使所有材料具有凝聚力。

原子核的质量大约是伴随它的电子的 5000 倍，因为质子或中子的质量大约是电子的 2000 倍，而且原子总是具有相同数量的质子和电子，以及数量大约等于或略大于质子数的中子（普通氢除外，它没有中子）。由于几乎所有的质量都由原子核（由质子和中子构成）承担，因此说电子是将原子核粘合在一起的胶水，而不是说原子核是将电子粘合在一起的胶水，更自然。

两个异性点电荷应该相互吸引，直到它们相遇。我们可以计算出它们以这种方式相互落下时可能提供的能量是无限的。但物质通常不会坍缩，并且它永远不会释放无限的能量。物体总是具有更低的能量状态，即它们的基态。在这种状态下，它们不能释放能量，因为它们没有更低的能量状态可以进入。原子、分子和离子处于基态或具有较高能量的激发态。气体越热，它的原子或分子就越激发。固体处于激发态，除非它的绝对温度为零开尔文。

要解释为什么氢原子中的电子不会落到质子上，或者更一般地说为什么材料不会坍缩，库仑定律是不够的，我们需要量子物理。

什么是电势差？

在稳态下，电势差是两点之间的电势差。它的测量单位是伏特 (V)。

什么是势？

要理解势，我们必须理解力的功。

我们可以用与理解重力势能相同的方式来理解电势。

我们可以毫不费力地将重物在冰面上移动，因为我们不必对抗重力。另一方面，垂直提起重物需要很大的努力，因为我们必须克服重力。在第一种情况下，重力不做功，因为运动是水平的。在第二种情况下，重力做功，因为运动是垂直的。

力 f 对直线运动的物体在长度 d 上所做的功 W 等于力向量 f 和位移向量 d 的标量积

W = f.d = f d cos $\theta$

其中 $\theta$ 是力向量 f 和位移向量 d 之间的夹角。f 和 d 是向量 f 和 d 的长度。

重力的方向是垂直的。它对水平位移不起作用，因为 cos 90° = 0。重力 $m\mathbf {g}$ 对质量 $m$ 所做的功为

$W=-mgh$

力的功就是能量。如果 $\theta$ > 90°，则 cos $\theta$ < 0，W < 0。力的功值为负，因为它是物体在力的作用下做功而损失的能量。这种能量损失可以是动能 E = 1/2 mv²。速度 v 降低，因为物体受到力的阻碍。如果 $\theta$ < 90°，则 cos $\theta$ > 0，W > 0。力的功值为正，因为它是物体在力的推动下加速运动而获得的能量。

在国际单位制（MKSA，米、千克、秒、安培）中，能量的单位是焦耳（J）。一焦耳是将物体在一牛顿（N）的力作用下移动一米所需的功。

1 J = 1 N. 1 m = 1 N.m

地球表面的重力约为 9.8 牛顿，几乎为 10 牛顿。因此，一焦耳大约是将一个 1 公斤的物体举高十厘米所需的能量。

当物体的轨迹为曲线时，我们通过在遵循曲线轨迹的折线上进行推理来计算力的功。如果线段的长度越来越短，折线就越来越接近它所遵循的曲线。我们通过取各线段上功的总和的极限来求力的功，当线段的长度趋于零时。力的功是力与位移向量在路径上的标量积的积分。

根据标量积的定义，重力 g 对斜线段 AB 所做的功等于 g(h_A - h_B)，其中 h_A - h_B 是其两端的高度差。现在，A 和 C 之间的高度差等于 A 和 B 之间的高度差与 B 和 C 之间的高度差之和

h_A - h_C = (h_A - h_B) + (h_B - h_C)

因此，重力 g 对任何从 A 到 Z 的路径所做的功始终等于 g(h_A - h_Z)。它只取决于端点 A 和 Z 的高度差，而与连接 A 和 Z 的路径无关。因此，我们在地球表面重力场的情况下证明了

定理：重力的功与所走的路径无关。

如果我们忽略摩擦力，则过山车上物体的动能就是从静止开始时重力的功。它只取决于高度差 $h$，而与所走的路径无关

力的功可能取决于所走的路径。例如，摩擦力的功随所走的路径越长而越大。

当一个力场使得力在两点之间的功与所走的路径无关时，我们可以引入一个势能。它的定义是选择一个零势能点。然后，空间中每个点的势能由力对一个标准物体从该点到零势能点所做的功来定义。对于重力，我们以质量为一的物体作为标准。对于电力，标准是电荷为一的物体。势能是明确定义的，因为力的功与所走的路径无关。

设 W_XY 是力对从 X 移动到 Y 的单位物体所做的功，V_X 是 X 点的势能，O 是零势能点。根据 V 的定义，V_A = W_AO，V_B = W_BO。所以 V_A - V_B = W_AO - W_BO。或者 W_AO = W_AB + W_BO。所以 V_A - V_B = W_AB。因此，两点之间的势能差始终等于力对从这两点之间移动的单位物体所做的功。

两点之间的电压是电力对从这两点之间移动的单位电荷所做的功。在稳态下，电力的功与所走的路径无关，因此这种力来自势能。电压就是势能差。它对于电力来说就像高度差对于重力一样。

电荷的单位是库仑。一伏特 (V) 是每库仑 (C) 一焦耳 (J)。这是给一个库仑的电荷一焦耳的能量所需的电压差。

1 V = 1 J/C

当在金属导线上施加电压时，电流通过导线，这是电子流。电子被电力加速，但它们的平均动能不会增加，因为它们被金属减速。它们通过焦耳效应将获得的所有能量损失给金属，从而使金属发热。电灯泡是通过将承载电流的金属丝加热到白炽状态而发明的。材料的电阻衡量其减缓通过它的电子或离子的能力。

势能

质量为 $m$ 的物体的重力势能等于 $mV_{X}$，其中 $V_{X}$ 是点 $X$ 的重力势。当物体静止时，它的能量不可见，不实际，因为它的动能为零。当静止的物体被释放到自由落体时，它的重力势能转化为动能。当物体静止时，能量已经存在，但它没有表现出来，它只是潜在的。它转化为动能是潜能的实现。

对于一个从静止状态释放的自由落体，其运动结束时的动能是其重力势能的实际体现，最初是不可见的。它等于重力所做的功。所以力的功是潜能的实现。势能是使力做功的潜力。当我们有可以用来做功的力时，我们就拥有潜能。

能量有许多形式：动能 ${\frac {1}{2}}mv^{2}$ 是质量 $m$ 由于其速度 $v$ 所具有的能量。热是原子和分子的动能。重力能、电能和核能分别是取决于重力、电和核力的势能。化学能是原子和分子的电能。光能是光粒子（光子）的动能。

动能方程 $E={\frac {1}{2}}mv^{2}$ 只是一个近似值。根据爱因斯坦的理论，相对论计算给出了更精确的结果。

重力势能转化为动能是能量守恒的一个例子。能量永远不会消失。当一个物体失去能量时，它总是把它传递给另一个物体，或者把它转化为另一种形式的能量。水力发电大坝将重力能转化为电能。电烤箱将电能转化为热能。核电站将核能转化为热能，再将热能转化为电能。所有形式的能源生产或消耗都是如此。宇宙中的总能量是恒定的。

质量的势能：E = mc²

即使是质量也是势能。

任何物体的质量 $m$ 与它被湮灭时可能释放的能量 $E$ 成正比

$m={\frac {E}{c^{2}}}$

或者

$E=mc^{2}$

其中 $c$ 是光速。

质量总是具有被湮灭的潜力。

方程 $E=mc^{2}$，由爱因斯坦于 1905 年发现，可以从电磁学的基本方程（麦克斯韦方程组）中推导出，麦克斯韦方程组于 1865 年被发现。它在本书最后一章中得到了解释和证明。

势的梯度

当力的功不依赖于所走的路径时，我们说力场来自一个势，因为我们可以通过对势取梯度来计算力。

要理解梯度的概念，最简单的方法是想象一座山的起伏。山坡上某一点的高度 h(x,y) 相对于海平面上的点 (x,y) 的高度是一个标量场。我们可以称它为高度场。从这个标量场我们可以定义一个向量场。对于每个点 (x,y)，我们定义一个向量 v(x,y)，其方向是该点山坡的最大倾斜线，方向向上，其长度是最大倾斜线的斜率（如果我们水平移动 100 米时上升了 10 米，则斜率等于 10% = 10/100 = 0.1）。这样定义的向量场就是高度场的梯度：v = grad h

在这些图像中，标量场用灰色阴影表示。它的梯度用箭头表示。如果标量场表示地形的起伏，第一个表示一个圆锥，第二个表示一个倾斜平面。

等高线是指等高线。如果 h 是一个势能，我们称它们为等势线。

最大倾斜线是指始终沿着最大倾斜方向延伸的线。它们始终在每个点都与向量场相切。如果 h 是一个势能，我们称它们为场线。

最大倾斜线始终垂直于等高线。同样，场线始终垂直于等势线。

黑线是场线，棕线是两个等量异号电荷产生的电场的等势线。

在地形图上，相邻的等高线始终表示相同的差值。它们越紧密，斜率越大。如果以同样的方式绘制相同电位差的相邻等势线，则线越紧密，场越大。

• 
• 

对于二维空间中的标量场 $h$，我们可以通过求其两个偏导数来计算其梯度。grad $h$ 的分量为 $\partial h/\partial x$ 和 $\partial h/\partial y$。

三维空间中标量场 $V$ 的梯度 grad $V$ 是一个向量场，其分量为 $\partial V/\partial x$，$\partial V/\partial y$ 和 $\partial V/\partial z$。

根据势能的定义，如果我们将标准物体移动 dx 的距离，其势能变化为 dV = -f_x dx，其中 f_x 是力 f 在 x 方向上的分量。因此 f_x = $-\partial V/\partial x$。类似地，f_y = $-\partial V/\partial y$ 和 f_z = - $\partial V/\partial z$。

作用在标准物体上的力 f 是势能 $V$ 梯度的反方向

f = -grad $V$

这是我们从势能计算力场的通用公式。

电荷产生的库仑势能

根据库仑定律，负电荷 -q 产生的电场 E 是指向电荷中心的矢量场，其大小为 q/r²，其中 r 是从该中心到该点的距离。对于正电荷 q，它是相同的场，只是矢量方向相反。

电荷 q 产生的电场 E 来自库仑势 V = q/r，其中 r 是从电荷中心到该点的距离。

E = -grad V = -grad q/r

等势面是以电荷为中心的球面。场线都是从电荷中心延伸出来的直线。

该势能在通过电荷的平面上可以用高度场表示。

等高线是等势线。它们是等势球面与通过电荷的平面的交线。

-dV/dr = q/r² = E，如果 q 是正电荷，则矢量 E 的长度。

电荷的库仑势与质量的万有引力势相似。

这些线是地球产生的万有引力场的场线，即重力场。

多个电荷产生的势能

多个电荷产生的电场是每个电荷单独产生的场的总和。现在，一个和的梯度是梯度的总和，因为 d(f+g)/dx = df/dx + dg/dx。因此，多个电荷产生的电场来自每个电荷单独产生的电势的总和。因此，我们证明了多个电荷产生的电场也来自一个势能。由于牛顿势能与库仑势在数学上相似，因此万有引力也一样。

产生两个相等且相反电荷的场可以用场线表示

以及等势线

或通过将它的势能表示为一个浮雕

我们也可以在空间中看到场线

地球和月球产生的万有引力势与两个负电荷产生的电势相同，这两个负电荷将具有与地球和月球质量成比例的电荷。

场线为蓝色，等势线为红色。

我们也可以用高度场来表示这个势能。

电容器的电荷

电容器由两个导电板组成，彼此非常靠近，并由绝缘材料隔开。每个端子连接到一个板。当电容器打开时，一个板会失去一些电子而带正电，而另一个板会获得电子而带负电。

我们用高斯定理（在麦克斯韦方程的章节中）证明了无限带电平面的电场力场 $\mathbf {E}$，其电荷密度是均匀的，等于 $\sigma$，在带电平面的每一边也是均匀的，垂直于它，其大小为 $E={\frac {\sigma }{2\epsilon _{0}}}$，如果它被真空包围，并且它在平面每一边的方向与其在另一边的方向相反。

由于多个电荷产生的电场是每个电荷产生的场的总和，因此两个表面电荷密度相等且相反的平行带电平面产生的电场在平面之间是均匀的，垂直于它们，其大小为

$E={\frac {\sigma }{\epsilon _{0}}}$

其中 $\sigma$ 是表面电荷密度的绝对值，

而在两个带电平面的外部空间中，它等于零。

有限表面电容器产生的场与前一个场相同，只是在边缘处不同。

电场力对平板之间的一个单位电荷所做的功等于 $Ed$，其中 $d$ 是它们的距离。对于远离边缘的完成的板，这仍然是正确的。因此，平板之间的电压 $V$ 与它们的电荷 $Q$ 成正比。因此，电荷与电压成正比。

$Q=CV$

其中 $C$ 是电容器的电容。 $C$ 度量了对于给定电压，一个板接收的电荷量。

$C={\frac {\epsilon _{0}S}{d}}$

对于表面积为$S$的平板，它们之间为真空，相距$d$。

证明：$C=Q/V={\frac {\sigma S}{Ed}}={\frac {\sigma S}{\sigma d/\epsilon _{0}}}={\frac {\epsilon _{0}S}{d}}$

这就是为什么我们要用表面积大、相互缠绕的导体板来制造电容器，并且用尽可能薄的绝缘薄膜将它们隔开。

$\epsilon _{0}$ 是真空介电常数。

如果平板之间用介电常数为 $\epsilon$ 的绝缘材料隔开，电容器的电容为

$C={\frac {\epsilon S}{d}}$

导电材料的静电学

当材料中包含可以自由移动的电荷时，该材料就是导电的。在金属中，这些电荷是导电电子。在半导体中，它们也可以是空穴，即电子海中缺失的电子，它们在电子海中移动。在盐水等离子溶液中，可移动的电荷是正离子和负离子。

在导电材料内部，静电场始终为零。

证明：如果场不为零，移动的电荷就会受到电力的作用而移动，场就不会是静止的。

另一方面，电荷可以积累在导电材料的表面。如果我们将一个金属物体放置在电荷附近，它的导电电子会移动以完全补偿从外部施加到金属内部的电场。从外部施加的场和积累在表面上的电子施加的场的总和在金属内部始终等于零。

在导电材料表面的外侧，电场垂直于表面。

证明：如果平行于表面的电场分量不为零，表面电荷就会移动以抵消它。

如果表面电荷密度为正，则表面电场从导电材料向外指向。如果它是负的，它就指向内部。

证明：如果相反，电力会将可移动电荷推入材料内部。

电场对表面电荷施加力，但不能使它们移动，因为它们不能从材料中移出。

在导电材料的表面，电场为

$E={\frac {\sigma }{\epsilon _{0}}}$

其中$\sigma$是表面电荷密度。

证明在麦克斯韦方程一章的关于高斯定理中给出。

电荷总是朝抵消它们运动原因的方向移动。两个相等且相反的电荷如果完全重叠，就会产生完全为零的电场。当它们相互吸引时，它们会朝抵消它们运动原因的电场的方向移动。

当电容器的端子连接到金属导线时，导电电子会受到电容器极板上的电荷施加的电力的作用，这会使它们朝放电方向移动，而不是朝电荷增加的方向移动。

电极化

当物体两点之间出现电荷差时，物体就被电极化了。

导电体在被放置在均匀的外部电场中时会被极化。物体两侧会出现相反的表面电荷。

绝缘体也会被均匀电场极化。两侧会出现表面电荷。这怎么可能呢，因为根据定义，绝缘体没有可以自由移动的电荷？

在绝缘体中，电子附着在原子核上。没有自由导电电子可以从一个原子核转移到另一个原子核。围绕它们所附着的原子核，电子保留了一点活动能力。它们可以集中在一边或另一边以补偿它们所受到的外部电力。我们可以将被困在原子或分子中的电子视为被原子核保留的电液体，可以变形。这就是为什么绝缘体像导电体一样可以被电场极化的原因。

在绝缘体内部，当它被均匀的外部场极化时，电荷会均匀地移动。因此，材料内部的电荷密度保持为零。表面电荷密度是唯一变化的。

绝缘体在极化时，正负电荷在绝缘体内部的移动是瞬态电流。但不能在绝缘材料中流动永久电流。

当物体被电极化时，它会朝施加的电力的方向定向

电荷系统的势能

如何计算电荷系统的电势能？

一个电荷$q$放置在电势$V$中，具有电势能$qV$。

如果我们使用公式$E_{p}=qV$将所有电荷的电势能加起来，我们得不到正确的结果。为什么？

为了计算系统的势能，我们必须计算组装系统时所消耗或获得的能量。 当我们组装电荷时，它们必须穿过的电场在组装开始和结束时并不相同。 当系统组装好后我们计算得到的势能 $V$，它不是电荷组装时遇到的电场的势能，它只是当新的电荷被带到系统附近时，它所遇到的电场的势能。

第一个组装的电荷不会遇到任何要被置于其中的电场力场，因为之前没有电荷存在。 第二个电荷遇到第一个电荷产生的电场。 第三个电荷遇到前两个电荷产生的电场，以此类推，直到最后一个电荷，它遇到所有先前电荷产生的电场。

示例：带电电容器的势能

为了给电容器充电，必须将电子从其一个极板移动到另一个极板。 第一个移动的电荷 $dq$ 没有遇到电场，因为电容器没有充电。 因此，移动它所必须做的功 $dW$ 为 $dW=0$。 如果电容器已经由电荷 $q=\int dq$ 充电，新的电荷 $dq$ 会遇到电场力场，因此它的起点和到达点之间存在电势差 $V_{2}-V_{1}={\frac {q}{C}}$。 所以

$dW=(V_{2}-V_{1})dq={\frac {q}{C}}dq$

$W=\int dW=\int {\frac {q}{C}}dq={\frac {1}{2}}CV^{2}$

$E_{p}={\frac {1}{2}}CV^{2}$ 因此是带电荷 $Q=CV$ 的电容器的电势能，其中 $C$ 是它的电容， $V$ 是它两极板之间的电势差。

电势能在哪里？

电势能归因于电荷。 这种能量是由电荷携带的吗？ 它位于电荷上吗？

$E=mc^{2}$。 质量总是能量。 能量总是具有质量。 本书末尾证明了这个方程，它表明被困在箱子里的光会增加箱子的质量。 因此，光具有与其能量除以 $c^{2}$ 相等的质量。

如果电势能局限于电荷上，它们能量的变化会导致它们的质量变化。 但是，这种效应从未被观察到。

电荷系统的电势能存在于它们产生电场的整个空间中，它是由电场携带的。 静电场 $\mathbf {E}$ 中的电能体积密度为

${\frac {dE_{p}}{dV}}={\frac {1}{2}}\epsilon _{0}\mathbf {E} ^{2}$

其中 $dE_{p}$ 是一个微小体积 $dV$ 内包含的电势能。

当我们将两个同种电荷靠近时，我们增加了电场的能量。

如果我们将两个异种电荷靠近，我们降低了电场的能量。原子核中质子和中子结合在一起的核力也是如此。我们要提供能量才能将它们分开。这就是为什么它们分离时质量比结合时更大的原因。

将构成质子或中子的三个夸克完全分开需要无限的能量。这就是为什么我们永远无法观察到孤立的夸克。

让我们证明 ${\frac {dE_{p}}{dV}}={\frac {1}{2}}\epsilon _{0}\mathbf {E} ^{2}$ 允许我们正确地计算带电电容器的电势能。

$E_{p}=\int _{V}dE_{p}=\int _{V}\epsilon _{0}\mathbf {E} ^{2}dV={\frac {Sd\sigma ^{2}}{2\epsilon _{0}}}$

其中 $S$ 是电容器的表面积，$d$ 是两极板之间的距离，$Sd$ 是两极板之间的体积，${\frac {\sigma }{\epsilon _{0}}}$ 是表面电荷密度 $\sigma$ 产生的电场 $E$。

现在

$C={\frac {\epsilon _{0}S}{d}}$$C={\frac {\epsilon _{0}S}{d}}$ 并且 $V=Ed={\frac {\sigma d}{\epsilon _{0}}}$

所以

$E_{p}={\frac {1}{2}}CV^{2}$

当我们定义电势时，我们可以自由选择零电势点。为了计算电场力，任何选择都是合适的，因为两个电势相差一个常数具有相同的梯度。但为了计算能量及其质量的存在，我们显然不能通过选择另一个零电势点来修改所有电荷的能量。零电势点必须选择得当，以便在不费力的情况下将电荷放置在那里。这就是为什么当我们计算电荷系统的静电能量时，我们假设它们放置在真空中，并在无穷远处定义零电势。电荷产生的力在无穷远处趋于零。如果我们离它们很远，就不会有任何力量与它们的电场力作斗争。

当偶极矩由等量异号电荷的分离产生时，例如当为电容器充电时，我们可以推理，就像电荷密度最初在任何地方都为零一样。因此，任何地方都没有电场力。因此，任何点都可以选择作为零电势点。