电动力学/电场

电场

电场是由带电物体产生的物理场，它影响附近带电物体在电场中的行为。电场无限地延伸到整个空间，描述了电相互作用。

使用库仑定律，我们可以将点电荷放置在相对于其他电荷的任何位置，并确定该点电荷上的力。电场是一个矢量场，其中空间中的每个点都被分配一个力向量，具体取决于场对该点电荷的影响。

数学表示

有多种数学方法可以表示电场。第一种方法将电场视为三维矢量场。该矢量场在空间和时间的每个点都有一个定义的值，因此通常被认为是空间和时间坐标的函数。因此，它通常写成 E(x, y, z, t)。如果该场是静电的，则通常会从描述中省略t项。此外，如果我们使用的是向量符号而不是笛卡尔坐标，我们可以将该场写成

$\mathbf {E} (\mathbf {r} )=\mathbf {E} (x,y,z)$

电场定义为点电荷q上力的极限，除以该点电荷的值，当电荷趋于零时。数学上

$\mathbf {E} (\mathbf {r} )=\lim _{q\to 0}{\frac {\mathbf {F} _{q}}{q}}$

我们取极限的原因非常重要：如果我们在系统中添加一个大于 0 的电荷，那么测试点电荷将影响系统并改变它。我们取极限并将测试电荷减小到零，以便它不会影响系统的其余部分。

使用我们的电荷密度函数 ρ，我们可以计算一个具有均匀电荷的大物体（如带电介质）对点电荷q施加的力。为此，我们将我们针对n个电荷的库仑定律扩展到具有连续电荷分布的类似定律

$\mathbf {E} =\int {\frac {\rho (\mathbf {r} ')(\mathbf {r} -\mathbf {r} ')}{4\pi \epsilon |\mathbf {r} -\mathbf {r} '|^{3}}}dV$

在场的每个点r处，都有一个由库仑定律给出的相关力。

电场（由点电荷引起）

另一种考虑E场的方法，而不是抽象的数学方程，是考虑单个点电荷。我们将点电荷放置在场的不同位置，并“测量”（使用库仑定律）场对点电荷的影响。我们可以使用这些测量结果来绘制等势线，即点电荷上的力相等的线。

在进行这些测量时，我们使用无限小的点电荷，因为在系统中添加非无限小的电荷会影响场，并对场中的其他粒子施加力。

静电场

如果电场 (E) 不为零，并且在时间上是恒定的，则该场被称为静电场。例如，如果以下关系成立，则该场为静电场

$\mathbf {E} (x,y,z,t_{1})=\mathbf {E} (x,y,z,t_{0})$

如果此等式对x、y、z、t₁ 和 t₀ 的所有值都成立，则该场为静电场。如果此等式不成立，则该场随时间变化，称为电动力学。

符号

我们知道电场是位置（以及可能的时间）的函数，因此在大多数应用中通常会省略所有参数。我们将在本书的其余部分使用粗体字母 E 表示电场。这是一种非常标准的电场符号，许多关于该主题的书籍会简单地将其称为 E 场，或简称“E 场”。我们也将在本书中遵循此惯例。

电场线

为了帮助我们可视化电场，我们使用一种称为电场线的图形符号。电场线是连接异号电荷的线。根据一般惯例，我们说电场线从正电荷发出，进入负电荷，如下所示

在绘制电场线时，我们有一些通用规则

1. 电场线不能交叉或重叠。
2. 电场线必须从正电荷开始，在负电荷结束。
3. 电场线应该均匀弯曲，并且不应有任何角度。

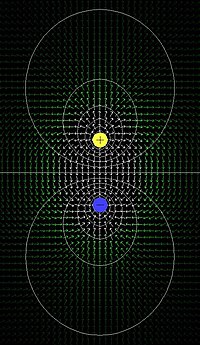
如果我们绘制所有电场线，我们将开始看到我们的电场。

势函数

对于静电场，旋度为零（可以验证）。这意味着力是保守的；存在一个势能函数，使得任何两点的势能差等于将电荷从一个点移动到另一个点的任何路径所需的功。

与电场一样，如果我们定义势能为场的属性，将是可取的。这将不再是势能；显然，电荷越大，移动它所需的功就越多。但是，我们可以定义一个势，它等于单位电荷的功，是场的固有属性。势的单位是焦耳每库仑。这在实际中使用如此普遍，以至于它被赋予了自己的名称，即伏特。

我们将φ(r) 设置为电场内位置的势函数。我们可以用 E 场来定义势函数

[势函数]

$\phi (\mathbf {r} )=\int _{\mathbf {r} \to \infty }\mathbf {E} \cdot dl$

或者，如果我们对两边求导，我们得到

$\nabla \phi (\mathbf {r} )=-\mathbf {E}$

通常，找到势函数比直接找到 E 场更容易。

使用高斯定律，我们可以将场的势函数与场中一点的电荷密度联系起来，如下所示

$\nabla ^{2}\phi =-\rho /\epsilon$

当我们讨论电能时，我们将更详细地讨论势函数。