电子学/模拟乘法器

模拟乘法器

模拟乘法器是一个电路，其输出与两个输入的乘积成正比

v_{out}=Kv_{1}\cdot v_{2}

其中 K 是一个常数，其量纲为电压的倒数。一般来说，我们可以预期两个输入可以是正的或负的，输出也可以是正的或负的。然而，大多数实现只在两个输入都严格为正时才有效：这不是一个很大的限制，因为我们可以对输入和输出进行偏移，使核心只处理正信号，而外部接口则可以处理任何极性（在特定配置下，在一定的限制范围内）。

将展示两种可能的实现方式。两种方法都将使用运算放大器，但第一种方法将使用二极管来获得所需的關係，第二种方法将使用 MOSFET 晶体管。

二极管实现

众所周知，使用运算放大器和二极管，很容易获得某个输入的对数和指数。记住对数的性质

\log(a\cdot b)=\log a+\log b

我们可以先计算两个信号的对数，然后将它们相加，最后计算该和的指数，从而实现两个信号的乘积。从数学的角度来看，只要两个输入为正数，这种方法就有效，因为负数的对数不存在（在实数域）。我们将会看到，即使原因更“物理”，这种限制对于实际电路也同样适用。这种实现的框图如下：

如果我们简单地将对数、求和和指数电路连接起来，我们将得到以下配置：

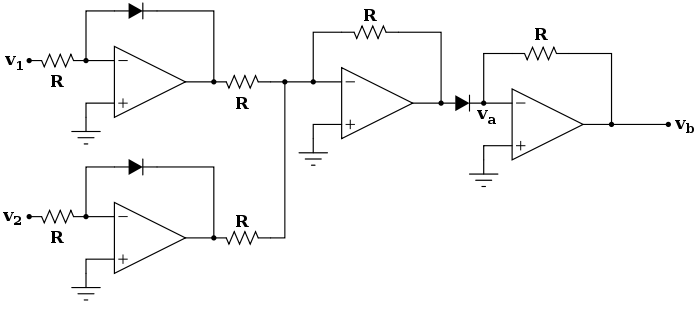
为了快速了解电路的行为，我们假设所有电阻 R 的值相同。显然，可以使用不同的值来获得不同的结果，但我们在这里不考虑这种情况。让我们使用以下符号来表示二极管电流和电压之间的关系：

i=I_{s}\left(e^{\frac {v}{V_{T}}}-1\right)

其中 $V_{T}={\frac {k*T}{q}}$ 是热电压（在常见的运行温度下为 25..30mV），I_s 是二极管反向偏置时的电流。如果我们在不引入任何近似的情况下分析电路，我们将得到

v_{a}=-\left[-V_{T}\ln \left({\frac {v_{1}}{RI_{s}}}+1\right)-V_{T}\ln \left({\frac {v_{2}}{RI_{s}}}+1\right)\right]=V_{T}\ln \left[\left({\frac {v_{1}}{RI_{s}}}+1\right)\left({\frac {v_{2}}{RI_{s}}}+1\right)\right]

因此，最终输出为

v_{b}=-RI_{s}\left(e^{\frac {v_{a}}{V_{T}}}-1\right)=-{\frac {v_{1}\cdot v_{2}}{RI_{s}}}-(v_{1}+v_{2})

很明显，输出结果中包含了我们想要的乘积，但也存在一个多余的项。不能简单地将其视为错误，因为它可能与乘积项一样大，因此必须将其移除。不过，这是一个简单的任务，只需要添加另一个阶段，使其精确地求和 $v_{1}+v_{2}$ ，这样就没有误差了。完整的乘法器电路如下：

其中输出电压由以下公式给出：

v_{out}=-\left(-{\frac {v_{1}\cdot v_{2}}{RI_{s}}}-(v_{1}+v_{2})+(v_{1}+v_{2})\right)={\frac {v_{1}\cdot v_{2}}{RI_{s}}}

这正是我们想要的。只要满足以下关系，电路就可以正常工作：

v_{1},v_{2}>-RI_{s}

因此，输入可以为零或略微负值，但由于 $RI_{s}$ 将是一个很小的电压，因此可以简单地将关系改写为 $v_{1},v_{2}\geq 0$ 。从数学的角度来看，这是因为我们无法计算负数的对数；从物理的角度来看，这个限制是由于我们只能获得极小的电流（几乎为零）反向偏置二极管。

在实际应用中，二极管被替换为以二极管方式工作的 BJT。

MOS 实现

由于可以将 MOSFET 晶体管用作电压控制电阻，因此可以利用此特性来创建模拟乘法器。参考右边的图片 - 字母表示不同的引脚：Drain（漏极）、Source（源极）和 Gate（栅极）。MOS 器件是对称的，因此漏极和源极可以互换，不会影响器件的行为。使用 _源极_ 作为最低电压端，使用 _漏极_ 作为最高电压端。当栅极和漏极之间的电压超过阈值电压时，即 $V_{GD}>V_{TH}$ ，电流和电压之间的关系如下：

I_{DS}=K[2(V_{GS}-V_{T})V_{DS}-V_{DS}^{2}]\simeq 2K(V_{GS}-V_{T})V_{DS};\qquad V_{GD}>>V_{TH}

假设我们始终可以使用这种关系，那么模拟乘法器的配置如下：

其中两个器件的源极和漏极都已标出。如果 $v_{2}$ 和 $V_{ref}$ 为正值，那么由运算放大器，源极将处于虚拟接地。流过 $R_{1}$ 的电流很明显：电阻的一端具有电压 $v_{1}$ ，另一端处于（虚拟）接地。相同的电流将流过 MOS $M_{2}$ ，从而确定电压 $V_{G}$ 。电流由以下公式给出：