
比较两个电压,并切换输出以指示哪个电压更大。

(其中  是电源电压,运放由
是电源电压,运放由  和
和  供电。)
供电。)
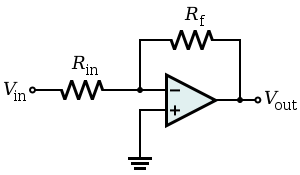
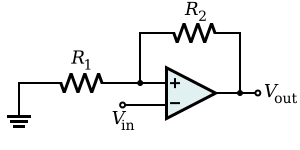
反向放大器使用负反馈来反转和放大电压。Rf 电阻允许部分输出信号返回到输入。由于输出与输入相位差 180°,因此该量实际上是从输入中减去的,从而减少了进入运算放大器的输入。这降低了放大器的整体增益,被称为负反馈。[1]

 (因为
(因为  是虚拟接地)
是虚拟接地)- 第三个电阻,其值为
 ,添加到非反相输入和地之间,虽然不是必需的,但它可以最大程度地减少由输入偏置电流引起的误差。[2]
,添加到非反相输入和地之间,虽然不是必需的,但它可以最大程度地减少由输入偏置电流引起的误差。[2]
放大器的增益由 Rf 与 Rin 的比率决定。也就是说

负号的存在是一种约定,表示输出被反转。例如,如果 Rf 是 10 000 Ω,而 Rin 是 1 000 Ω,则增益将是 -10 000Ω/1 000Ω,即 -10。[3]
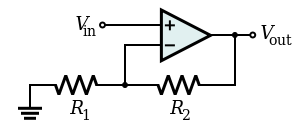
放大电压(乘以大于 1 的常数)

- 输入阻抗

- 输入阻抗至少为非反相 (
 ) 和反相 (
) 和反相 ( ) 输入之间的阻抗,通常为 1 MΩ 到 10 TΩ,再加上反相 (
) 输入之间的阻抗,通常为 1 MΩ 到 10 TΩ,再加上反相 ( ) 输入到地 (即
) 输入到地 (即  与
与  并联) 的阻抗。
并联) 的阻抗。
- 由于负反馈确保非反相和反相输入匹配,因此输入阻抗实际上要高得多。
- 虽然该电路具有较大的输入阻抗,但它会受到输入偏置电流误差的影响。
- 非反相 (
 ) 和反相 (
) 和反相 ( ) 输入会将小的漏电流引入运算放大器。
) 输入会将小的漏电流引入运算放大器。
- 这些输入电流会产生电压,这些电压就像未建模的输入偏移量。这些未建模的影响会导致输出上的噪声 (例如,偏移量或漂移)。
- 假设两个泄漏电流是匹配的,可以通过确保每个输入的直流阻抗相同来减轻它们的影响。
- 每个偏置电流产生的电压等于偏置电流与每个输入的等效直流阻抗的乘积。使这些阻抗相等会使每个输入的偏移电压相等,因此非零偏置电流不会影响两个输入之间的差值。
- 一个值为

- 的电阻,即
 与
与  并联的等效电阻,连接在
并联的等效电阻,连接在  源和非反相 (
源和非反相 ( ) 输入之间,将确保每个输入的输出阻抗匹配。
) 输入之间,将确保每个输入的输出阻抗匹配。
- 然后,匹配的偏置电流将产生匹配的偏移电压,只要 CMRR 良好,它们的影响就会对运算放大器 (它作用于其输入之间的差值) 隐藏起来。
- 通常,输入电流是不匹配的。
- 大多数运算放大器提供了一些平衡两个输入电流的方法 (例如,通过外部电位器)。
- 或者,可以向运算放大器输入添加外部偏移量以抵消其影响。
- 另一种解决方案是在
 源和非反相 (
源和非反相 ( ) 输入之间插入一个可变电阻。可以调整电阻,直到每个输入的偏移电压匹配。
) 输入之间插入一个可变电阻。可以调整电阻,直到每个输入的偏移电压匹配。
- 具有基于 MOSFET 的输入级运算放大器的输入电流非常小,通常可以忽略。

所示电路用于找到两个电压的差值,每个电压都乘以某个常数 (由电阻决定)。
"差分放大器" 这个名称不应该与本页也显示的 "微分器" 混淆。

- 差分
 (两个输入引脚之间) =
(两个输入引脚之间) =  (注意:这是一个近似值)
(注意:这是一个近似值)
对于共模抑制,对一个输入所做的任何操作都必须对另一个输入进行。例如,在 Rf 并联添加补偿电容,必须在 Rg 并联添加等效电容。
仪表放大器也是一种差分放大器,它也提供高输入阻抗,该放大器也在本页中显示。
只要  并且
并且  ,差分增益为
,差分增益为
 并且
并且 
当  并且
并且  ,差分增益为 A = 1,电路充当差分跟随器
,差分增益为 A = 1,电路充当差分跟随器


用作缓冲放大器,以消除负载效应(例如,将具有高源阻抗的器件连接到具有低输入阻抗的器件)。

 (实际上,运算放大器本身的差分输入阻抗,1 MΩ 到 1 TΩ)
(实际上,运算放大器本身的差分输入阻抗,1 MΩ 到 1 TΩ)
由于强(即,单位增益)反馈和真实运算放大器的某些非理想特性,该反馈系统容易出现较差的稳定性裕度。因此,当连接到足够大的容性负载时,系统可能不稳定。在这些情况下,可以使用滞后补偿网络(例如,通过电阻器将负载连接到电压跟随器)来恢复稳定性。运算放大器的数据手册可能提供外部补偿网络中组件选择的指导。或者,可以选择具有更合适的内部补偿的另一种运算放大器。
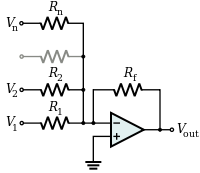
求和放大器将多个(加权)电压相加

- 当
 ,且
,且  独立
独立

- 当


- 输出反转
- 第 n 个输入的输入阻抗为
 (
( 是虚拟地)
是虚拟地)
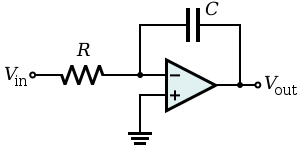
对 (反转) 信号进行时间积分

(其中  和
和  是时间的函数,
是时间的函数, 是积分器在时间 t = 0 时的输出电压。)
是积分器在时间 t = 0 时的输出电压。)
- 请注意,这也可以看作一个低通电子滤波器。它是一个在直流 (即
 ) 处具有单极点和增益的滤波器。
) 处具有单极点和增益的滤波器。
- 此电路存在一些潜在问题。
- 通常假设输入
 的直流分量为零(即平均值为零)。否则,除非电容器周期性地放电,否则输出将漂移到运算放大器的工作范围之外。
的直流分量为零(即平均值为零)。否则,除非电容器周期性地放电,否则输出将漂移到运算放大器的工作范围之外。
- 即使
 没有偏移,运算放大器输入端的泄漏电流或偏置电流也会在
没有偏移,运算放大器输入端的泄漏电流或偏置电流也会在  上添加一个意外的偏移电压,从而导致输出漂移。平衡输入电流 **和** 用一个阻值为
上添加一个意外的偏移电压,从而导致输出漂移。平衡输入电流 **和** 用一个阻值为  的电阻替换非反相 (
的电阻替换非反相 ( ) 短路接地,可以降低此问题的严重程度。
) 短路接地,可以降低此问题的严重程度。
- 由于此电路没有提供直流反馈(即电容器对
 的信号看起来像开路),输出的偏移可能与预期不符(即,
的信号看起来像开路),输出的偏移可能与预期不符(即, 可能会超出设计者在当前电路中的控制范围)。
可能会超出设计者在当前电路中的控制范围)。
- 通过在反馈电容器并联添加一个大电阻
 可以降低许多这些问题的严重程度。在极高的频率下,此电阻的影响可以忽略不计。但是,在低频下,存在漂移和偏移问题,该电阻提供必要的反馈以将输出稳定在正确的值。实际上,此电阻降低了“积分器”的直流增益——从无穷大变为某个有限值
可以降低许多这些问题的严重程度。在极高的频率下,此电阻的影响可以忽略不计。但是,在低频下,存在漂移和偏移问题,该电阻提供必要的反馈以将输出稳定在正确的值。实际上,此电阻降低了“积分器”的直流增益——从无穷大变为某个有限值  .
.

对(反相)信号进行时间微分。

- 请注意,这也可以看作一个高通电子滤波器。它是一个在直流 (即
 ) 处具有单零点和增益的滤波器。微分放大器的高通特性会导致电路在模拟伺服回路中使用时出现不稳定行为。出于这个原因,系统函数将被重新制定以使用积分器。
) 处具有单零点和增益的滤波器。微分放大器的高通特性会导致电路在模拟伺服回路中使用时出现不稳定行为。出于这个原因,系统函数将被重新制定以使用积分器。
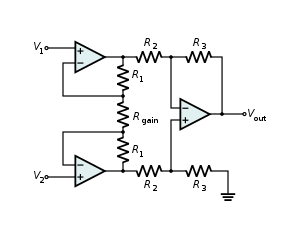
它结合了非常高的输入阻抗、高共模抑制比、低直流偏移以及其他在进行非常精确、低噪声测量中使用的特性。
- 它是在差分放大器的每个输入端添加一个非反相缓冲器来增加输入阻抗而制成的。
一个双稳态多谐振荡器,实现为具有滞后的比较器。

在此配置中,输入电压通过电阻  (可能是电源内部电阻)施加到同相输入端,反相输入端接地或参考。滞回曲线为非反相,切换阈值为
(可能是电源内部电阻)施加到同相输入端,反相输入端接地或参考。滞回曲线为非反相,切换阈值为  ,其中
,其中  是运算放大器的最大输出幅度。
是运算放大器的最大输出幅度。
或者,可以交换输入源和地。现在,输入电压直接施加到反相输入端,同相输入端接地或参考。滞回曲线为反相,切换阈值为  。这种配置用于下面所示的弛豫振荡器。
。这种配置用于下面所示的弛豫振荡器。
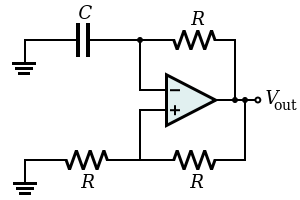
通过使用RC网络向反相施密特触发器添加缓慢的负反馈,形成了弛豫振荡器。RC网络的反馈使施密特触发器输出以无限的对称方波振荡(即,在此配置中,施密特触发器是一个非稳态多谐振荡器)。

模拟电感(即,在不使用可能昂贵的电感的情况下提供电感)。该电路利用了流过电容器的电流随时间变化与电感两端的电压相同的特性。该电路中使用的电容器小于它模拟的电感,并且它的电容受环境变化影响的程度较小。
该电路不适合依赖电感反电动势特性的应用,因为这将在模拟器电路中限制为运算放大器的电源电压。
分压器参考
- 齐纳二极管设定参考电压。
- 充当一个输入端接地的比较器。
- 当输入为零时,运算放大器输出为零(假设电源电压对称)。

为任何信号发生器创建一个具有负值的电阻。
- 在这种情况下,输入电压与输入电流之间的比率(因此是输入电阻)由以下公式给出:

通常,元件  、
、 和
和  不必是电阻器;它们可以是任何可以用阻抗描述的元件。
不必是电阻器;它们可以是任何可以用阻抗描述的元件。

产生非常低的失真正弦波。使用灯泡或二极管形式的负温度补偿。
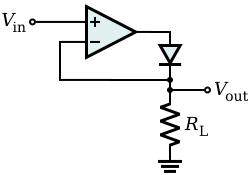
无源整流器电路中,正向偏置二极管上的压降VF 是不希望的。在这个有源版本中,通过将二极管连接到负反馈回路来解决这个问题。运算放大器将负载两端的输出电压与输入电压进行比较,并将其自身的输出电压提高VF 的值。因此,压降VF 被补偿,电路的行为非常接近理想的(超级)二极管,VF = 0 V。
由于缓慢的负反馈,以及许多非理想运算放大器本身的低压摆率,该电路在高频下存在速度限制。
- 另请参阅:对数放大器
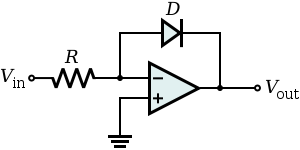
- 输入电压
 和输出电压
和输出电压  之间的关系由下式给出:
之间的关系由下式给出:

- 其中
 是饱和电流,
是饱和电流, 是热电压。
是热电压。
- 如果运算放大器被认为是理想的,则负极虚拟接地,因此从电源流入电阻的电流(以及因此通过二极管到输出端,因为运算放大器输入端没有电流)为

- 其中
 是通过二极管的电流。众所周知,二极管的电流和电压之间的关系为
是通过二极管的电流。众所周知,二极管的电流和电压之间的关系为

- 当电压大于零时,这可以近似为

- 将这两个公式放在一起,并考虑到输出电压是二极管电压的负值 (
 ),该关系得以证明。
),该关系得以证明。
请注意,此实现没有考虑温度稳定性和其他非理想影响。

- 输入电压
 和输出电压
和输出电压  之间的关系由下式给出:
之间的关系由下式给出:

其中  是饱和电流,
是饱和电流, 是热电压。
是热电压。
- 考虑到运算放大器是理想的,则负极虚拟接地,因此通过二极管的电流由下式给出:

当电压大于零时,它可以近似为

输出电压由下式给出:

- ↑ Delton T. Horn 撰写《基本电子学理论》,第 4 版。McGraw-Hill 专业版,1994 年,第 342-343 页。
- ↑ Malmstadt,Enke 和 Crouch,科学家使用的电子学和仪器,本杰明/卡明斯出版公司,1981 年,ISBN 0-8053-6917-1,第 5 章。第 118 页。
- ↑ 基本电子学理论,Delton T. Horn,第 4 版。麦格劳-希尔专业,1994 年,第 342-343 页。

















































































