电子学/扩展版共振

< 扩展版

共振

简单的共振电路，描述。

滤波器

理想滤波器

(讨论理想滤波器如何提供信号直到截止频率，然后提供总衰减。也就是说，它们看起来像一个 $u(\omega )-uu(\omega -\omega _{c})$ 对于低通滤波器，其中 u(w) 是单位阶跃函数或 Heaviside 函数。也就是说，它们在截止频率处有无限的下降。如何实现这一点是不可能的。漂亮的低通、高通、带通、带阻滤波器图表。）

图 1：理想低通滤波器的传递函数。

图 2：理想高通滤波器的传递函数。

图 3：理想带通滤波器的传递函数。

图 4：理想带阻滤波器的传递函数。

本节介绍一阶巴特沃斯低通和高通滤波器。理解拉普拉斯变换，或者至少理解电容、电感和电阻的拉普拉斯变换。

低通

图 1：基本的 RC 电路。

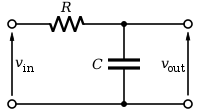
将电阻和电容变换到拉普拉斯域，我们得到

R 和 ${\frac {1}{Cs}}$.

用 $V_{in}(s)$ 表示 $V_{out}(s)$.

$V_{out}(s)={\frac {V_{in}(s){\frac {1}{Cs}}}{R+{\frac {1}{Cs}}}}$

$V_{out}(s)={\frac {V_{in}(s)}{RCs+1}}$

传递函数是

$H(s)={\frac {V_{out}(s)}{V_{in}(s)}}$

所以

$H(s)={\frac {1}{RCs+1}}$

对于频域，我们将 $s=j\omega$

$H(\omega )={\frac {1}{jRC\omega +1}}$

幅值为

$|H(\omega )|={\frac {1}{\sqrt {R^{2}C^{2}\omega ^{2}+1}}}$

相位为

$<H(\omega )=-arctan(RC\omega )\,$

随着$\omega$的增加，$|H(j\omega )|$降低，所以该电路必须代表低通滤波器。

使用-3dB带宽定义。 $|H(j\omega )|={\frac {1}{\sqrt {2}}}$

${\frac {1}{\sqrt {2}}}={\frac {1}{\sqrt {R^{2}C^{2}\omega ^{2}+1}}}$

因此

$2=R^{2}C^{2}\omega ^{2}+1$

$\omega ={\frac {1}{RC}}$

这给出了低通巴特沃斯滤波器的一般形式为

$|H(\omega )|={\frac {1}{\sqrt {1+({\frac {\omega }{\omega _{c}}})^{2k}}}}$

, 其中k是滤波器的阶数，$\omega _{c}$是截止频率。

高通

(一阶RL高通滤波器的图像)

如果电路的所有元件都转换到拉普拉斯域。电阻变为$R$，电感变为$Ls$。使用电压分配规则，可以得到下面的$H(s)$。

$H(s)={\frac {\frac {Rs}{L}}{1+{\frac {Rs}{L}}}}$

如果$H(s)$通过将$s=j\omega$代入转换到频域。

$H(\omega )={\frac {\frac {j\omega R}{L}}{1+{\frac {j\omega R}{L}}}}$

其幅值为

$|H(\omega )|={\frac {\sqrt {\frac {\omega ^{2}R^{2}}{L^{2}}}}{\sqrt {1+{\frac {\omega R^{2}}{L^{2}}}}}}$

其相位为

$<H(\omega )=90-\arctan({\frac {\omega R}{L}})$

(截止频率为 w (R/L)^0.5)